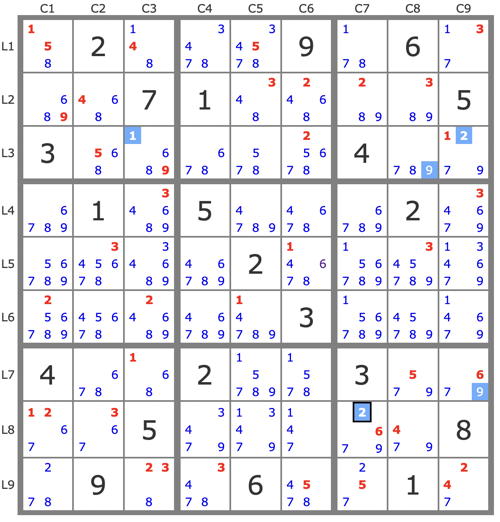
- Code: Select all
. 2 . . . 9 . 6 .
. . 7 1 . . . . 5
3 . . . . . 4 . .
. 1 . 5 . . . 2 .
. . . . 2 . . . .
. . . . . 3 . . .
4 . . 2 . . 3 . .
. . 5 . . . . . 8
. 9 . . 6 . . 1 .
.2...9.6...71....53.....4...1.5...2.....2.........3...4..2..3....5.....8.9..6..1.
158 2 148 3478 34578 9 178 6 137
689 468 7 1 348 2468 289 389 5
3 568 1689 678 578 25678 4 789 1279
6789 1 34689 5 4789 4678 6789 2 34679
56789 345678 34689 46789 2 14678 156789 345789 134679
256789 45678 24689 46789 14789 3 156789 45789 14679
4 678 168 2 15789 1578 3 579 679
1267 367 5 3479 13479 147 2679 479 8
278 9 238 3478 6 4578 257 1 247
Puzzle 29
5 posts
• Page 1 of 1
Puzzle 29
another puzzle without rc-bivalue at the start and this time without 1-Backdoor and 1-antiBackdoor after singles + intersections; my solution is 4 not too long chains.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 29
Hi P.O.,
I don't see the backdoor, but anyway, here is my resolution (with TDP).
P(2r8c7) : [ 2r8c7->2r3c9->1r3c3->9r3c8 ]->9r7c9->... => 6b9 empty => r8c7≠2 => r8c1=2 + 10 placements and basic eliminations.
P(3r9c4) : 3r9c4->[ 4r9c6 & 3r2c5 & 8r9c3->8r2c2 ]->9r2c8->6r2c1->... r2c6 empty => r9c4≠3 => r9c3=3 + 22 placements.
P'(9r4c5) : (-9r4c5)->9r7c5->8r7c6->[ 7r5c6 & 5r7c8 ]->8r5c8->8r4c3->... => -78r4c5 => r4c5=9, stte.
Robert
I don't see the backdoor, but anyway, here is my resolution (with TDP).
P(2r8c7) : [ 2r8c7->2r3c9->1r3c3->9r3c8 ]->9r7c9->... => 6b9 empty => r8c7≠2 => r8c1=2 + 10 placements and basic eliminations.
puzzle3: Show
P(3r9c4) : 3r9c4->[ 4r9c6 & 3r2c5 & 8r9c3->8r2c2 ]->9r2c8->6r2c1->... r2c6 empty => r9c4≠3 => r9c3=3 + 22 placements.
puzzle3: Show
P'(9r4c5) : (-9r4c5)->9r7c5->8r7c6->[ 7r5c6 & 5r7c8 ]->8r5c8->8r4c3->... => -78r4c5 => r4c5=9, stte.
puzzle3: Show
Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: Puzzle 29
hi Robert, i realize that i didn't express myself clearly; i wrote without '1-backdoor' meaning there is no one candidate that if set solves the puzzle after applying singles + intersections, same for '1-antibackdoor'; but there are '2-backdoors' and '2-antibackdoors', meaning 2 candidates that if set or removed solve the puzzle.
i found 9 2-AntiBackdoors:
(((((1 9 3) (1 3 7)) 3) (((7 9 9) (6 7 9)) 6) S)
((((2 5 2) (3 4 8)) 3) (((7 9 9) (6 7 9)) 6) S)
((((4 3 4) (3 4 6 8 9)) 3) (((7 9 9) (6 7 9)) 6) S)
((((5 8 6) (3 4 5 7 8 9)) 3) (((7 9 9) (6 7 9)) 6) S)
((((7 9 9) (6 7 9)) 6) (((8 2 7) (3 7)) 3) S)
((((7 9 9) (6 7 9)) 6) (((9 1 7) (7 8)) 7) S)
((((7 9 9) (6 7 9)) 6) (((9 3 7) (3 8)) 8) S)
((((7 9 9) (6 7 9)) 6) (((9 4 8) (3 4 7 8)) 3) S)
((((7 9 9) (6 7 9)) 6) (((9 6 8) (4 5 7 8)) 4) S))
and 167 2-Backdoors, here are the first:
(((((1 1 1) (1 5 8)) 1) (((4 7 6) (6 7 8 9)) 7) Z)
((((1 1 1) (1 5 8)) 1) (((5 1 4) (5 6 7 8 9)) 7) S)
((((1 1 1) (1 5 8)) 1) (((5 8 6) (3 5 7 8 9)) 5) S)
((((1 1 1) (1 5 8)) 1) (((8 2 7) (3 6 7)) 7) S)
((((1 1 1) (1 5 8)) 1) (((9 6 8) (4 5 7 8)) 7) S)
((((1 3 1) (1 4 8)) 4) (((8 2 7) (3 6 7)) 7) Z)
((((1 4 2) (3 4 7 8)) 3) (((6 9 6) (1 4 6 7 9)) 6) S)
((((1 4 2) (3 4 7 8)) 3) (((7 2 7) (6 7 8)) 6) S)
((((1 4 2) (3 4 7 8)) 3) (((7 5 8) (1 5 7 8 9)) 8) S)
((((1 4 2) (3 4 7 8)) 3) (((7 9 9) (6 7 9)) 9) S)
.....
i found 9 2-AntiBackdoors:
(((((1 9 3) (1 3 7)) 3) (((7 9 9) (6 7 9)) 6) S)
((((2 5 2) (3 4 8)) 3) (((7 9 9) (6 7 9)) 6) S)
((((4 3 4) (3 4 6 8 9)) 3) (((7 9 9) (6 7 9)) 6) S)
((((5 8 6) (3 4 5 7 8 9)) 3) (((7 9 9) (6 7 9)) 6) S)
((((7 9 9) (6 7 9)) 6) (((8 2 7) (3 7)) 3) S)
((((7 9 9) (6 7 9)) 6) (((9 1 7) (7 8)) 7) S)
((((7 9 9) (6 7 9)) 6) (((9 3 7) (3 8)) 8) S)
((((7 9 9) (6 7 9)) 6) (((9 4 8) (3 4 7 8)) 3) S)
((((7 9 9) (6 7 9)) 6) (((9 6 8) (4 5 7 8)) 4) S))
and 167 2-Backdoors, here are the first:
(((((1 1 1) (1 5 8)) 1) (((4 7 6) (6 7 8 9)) 7) Z)
((((1 1 1) (1 5 8)) 1) (((5 1 4) (5 6 7 8 9)) 7) S)
((((1 1 1) (1 5 8)) 1) (((5 8 6) (3 5 7 8 9)) 5) S)
((((1 1 1) (1 5 8)) 1) (((8 2 7) (3 6 7)) 7) S)
((((1 1 1) (1 5 8)) 1) (((9 6 8) (4 5 7 8)) 7) S)
((((1 3 1) (1 4 8)) 4) (((8 2 7) (3 6 7)) 7) Z)
((((1 4 2) (3 4 7 8)) 3) (((6 9 6) (1 4 6 7 9)) 6) S)
((((1 4 2) (3 4 7 8)) 3) (((7 2 7) (6 7 8)) 6) S)
((((1 4 2) (3 4 7 8)) 3) (((7 5 8) (1 5 7 8 9)) 8) S)
((((1 4 2) (3 4 7 8)) 3) (((7 9 9) (6 7 9)) 9) S)
.....
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 29
- Code: Select all
+----------------------------+--------------------------+-----------------------------+
| d158 2 d148 | 3478 34578 9 | 178 6 137 |
| 689 d468 7 | 1 348 2468 | 289 389 5 |
| 3 d568 689-1 | 678 578 25678 | 4 789 1279 |
+----------------------------+--------------------------+-----------------------------+
| 6789 1 34689 | 5 4789 4678 | 6789 2 34679 |
| 56789 345678 34689 | 46789 2 14678 | 156789 345789 134679 |
| 256789 45678 24689 | 46789 14789 3 | 156789 45789 14679 |
+----------------------------+--------------------------+-----------------------------+
| 4 678 a168 | 2 15789 1578 | 3 579 679 |
| b1267 c367 5 | 3479 13479 147 | b2679 479 8 |
| 278 9 238 | 3478 6 4578 | 257 1 247 |
+----------------------------+--------------------------+-----------------------------+
1. (1)r7c3 = (12-6)r8c17 = r8c2 - (6=4581) =>-1r3c3; 11 placements & ls
- Code: Select all
+-------------------------+--------------------------+--------------------------+
| 1 2 a48 | 3478 5 9 | 78 6 37 |
| 69 b48 7 | 1 c348 x468 | 2 389 5 |
| 3 5 69 | 678 78 2 | 4 789 1 |
+-------------------------+--------------------------+--------------------------+
| 6789 1 34689 | 5 4789 4678 | 6789 2 34679 |
| 56789 3478 34689 | 46789 2 14678 | 156789 3578 34679 |
| 56789 478 2 | 46789 14789 3 | 156789 578 4679 |
+-------------------------+--------------------------+--------------------------+
| 4 678 1 | 2 789 578 | 3 57 69 |
| 2 367 5 | 379 c1379 17 | 69 4 8 |
| 78 9 a38 | z478-3 6 y4578 | 57 1 2 |
+-------------------------+--------------------------+--------------------------+
2. Almost ALS M-Wing:
[(3=84)r19c3 - r2c2 *=* (43)r28c5] = (4)r2c6 - r9c6 = (4)r9c4 => -3r9c4; 23 placements
- Code: Select all
+------------------+---------------------+--------------------+
| 1 2 4 | 3 5 9 | 8 6 7 |
| 9 8 7 | 1 4 6 | 2 3 5 |
| 3 5 6 | 78 78 2 | 4 9 1 |
+------------------+---------------------+--------------------+
| 67 1 b89# | 5 a789* 4 | a679* 2 3 |
| 567 3 c89 | 6789 2 c78 | 1 c578 4 |
| 567 4 2 | 6789 1 3 | 5679 578 69 |
+------------------+---------------------+--------------------+
| 4 d67 1 | 2 78-9 578 | 3 d57 d69 |
| 2 67 5 | a79* 3 1 | a69* 4 8 |
| 8 9 3 | 4 6 57 | 57 1 2 |
+------------------+---------------------+--------------------+
3. Almost kite:
[(9)r8c4 = r8c7 - r4c7 *=* r4c5] = (9)r4c3-(9=785)r5c368-(5=769)r7c8 => -9 r7c5; ste
Cenoman
- Cenoman
- Posts: 3211
- Joined: 21 November 2016
- Location: France
Re: Puzzle 29
thank you for your solutions, they made me change mine; your second step eliminates n3r9c4 and gets all the placements i needed 2 chains for, so i looked for a way to do the same elimination and i found an unit forcing chain;
here is my 3 steps solution:
here is my 3 steps solution:
- Code: Select all
da±1(58) 2 e+148 3478 34578 9 ×178 6 ×137
689 d(48)6 7 1 348 2468 289 389 5
3 d(58)6 ×1689 678 578 25678 4 789 1279
6789 1 34689 5 4789 4678 6789 2 34679
56789 345678 34689 46789 2 14678 156789 345789 134679
256789 45678 24689 46789 14789 3 156789 45789 14679
4 678 168 2 15789 1578 3 579 679
a+1267 c3+67 5 3479 13479 147 b+2679 479 8
278 9 238 3478 6 4578 257 1 247
c1n1{r1 r8} - r8n2{c1 c7} - r8n6{c7 c2} - b1{r1c1r2c2r3c2}{n4n5n8} - r1c3{n4n8 n1} => r1c7 r1c9 r3c3 <> 1
singles: ( n5r1c5 n5r3c2 n1r1c1 n1r7c3 n2r6c3 n2r8c1 n4r8c8 n2r3c6 n2r2c7 n2r9c9 n1r3c9 )
intersections: c8n9{r2r3} => r5c8 r6c8 r7c8 <> 9
c2n6{r7r8} => r2c2 r5c2 r6c2 <> 6
1 2 b4+8 3478 5 9 78 6 37
689 a+48 7 1 A3+48 x+468 2 389 5
3 5 689 678 78 2 4 789 1
6789 1 34689 5 4789 4678 6789 2 34679
56789 3478 34689 46789 2 14678 156789 3578 34679
56789 478 2 46789 14789 3 156789 578 4679
4 678 1 2 789 578 3 57 679
2 367 5 379 B1+379 17 679 4 8
78 9 c+38 y×3+478 6 y-4578 57 1 2
r2n4{c2c5c6} => r9c4 <> 3
r2n4{c5c6 c2} - r1c3{n4 n8} - r9c3{n8 n3}
r2n4{c2c6 c5} - c5n3{r2 r8}
r2n4{c2c5 c6} - r9n4{c6 c4}
singles: ( n4r9c4 n4r5c9 n1r5c7 n4r6c2 n4r4c6 n3r5c2 n3r4c9 n1r6c5 n1r8c6 n8r9c1 n3r8c5 n3r9c3 n3r1c4 n9r3c8 n8r1c7 n7r1c9 n6r3c3 n3r2c8 n9r2c1 n6r2c6 n8r2c2 n4r1c3 n4r2c5 )
1 2 4 3 5 9 8 6 7
9 8 7 1 4 6 2 3 5
3 5 6 78 78 2 4 9 1
67 1 89 5 e78+9 4 679 2 3
567 3 89 6789 2 a7A8 1 578 4
567 4 2 d67+89 1 3 5679 c5+78 69
4 67 1 2 B7+8×9 B57-8 3 c5-7 69
2 67 5 79 3 1 679 4 8
8 9 3 4 6 b5-7 b5+7 1 2
r5c6{n7n8} => r7c5 <> 9
r5c6{n8 n7} - r9n7{c6 c7} - c8n7{r7 r6} - r6n8{c8 c4} - r4c5{n7n8 n9}
r5c6{n7 n8} - r7n8{c6 c5}
ste.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
5 posts
• Page 1 of 1