The New Sudoku Players' Forum

[P.O.]

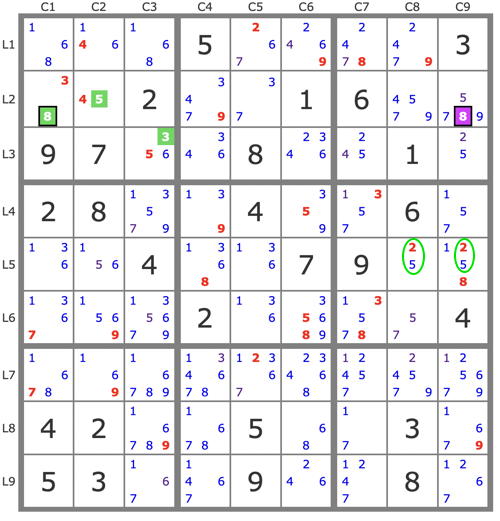
another puzzle with the same pattern as the previous one, just a little more difficult:

Code: Select all

. . .   5 . .   . . 3
. . 2   . . 1   6 . .
9 7 .   . 8 .   . 1 .
2 8 .   . 4 .   . 6 .
. . 4   . . 7   9 . .
. . .   2 . .   . . 4
. . .   . . .   . . .
4 2 .   . 5 .   . 3 .
5 3 .   . 9 .   . 8 .

...5....3..2..16..97..8..1.28..4..6...4..79.....2....4.........42..5..3.53..9..8.


[Leren]

Code: Select all

*------------------------------------------------------------------*
|b168   b146  b168    | 5       267   2469  | 2478   2479   3      |
|b38   cb45    2      |c3479   c37    1     | 6     c4579  c5789   |
| 9      7     356    | 346     8     2346  | 245    1      25     |
|---------------------+---------------------+----------------------|
| 2      8     13579  | 139     4     359   | 1357   6      157    |
|a136   a156   4      |a1368   a136   7     | 9      25     125-8  |
| 1367   1569  135679 | 2       136   35689 | 13578  57     4      |
|---------------------+---------------------+----------------------|
| 1678   169   16789  | 134678  12367 23468 | 12457  24579  125679 |
| 4      2     16789  | 1678    5     68    | 17     3      1679   |
| 5      3     167    | 1467    9     246   | 1247   8      1267   |
*------------------------------------------------------------------*

ALS XY Wing: (8=5) r5c1245 - (5=3) r1c123, r2c12 - (3=8) r2c24589 => - 8 r5c9; basics;

Code: Select all

*---------------------------------------------------------*
| 168  146   168   | 5     26  2469  | 247    2479  3     |
| 3    45    2     | 49    7   1     | 6      459   8     |
| 9    7     56    | 346   8   2346  | 245    1     25    |
|------------------+-----------------+--------------------|
| 2    8     1579  | 19    4   59    | 3      6     157   |
| 6-1  56-1  4     | 8     3   7     | 9     b25   b125   |
|a17   159   3     | 2     16  569   | 8     b57    4     |
|------------------+-----------------+--------------------|
| 1678 169   16789 | 13467 126 23468 | 12457  2457  25679 |
| 4    2     16789 | 167   5   68    | 17     3     679   |
| 5    3     167   | 1467  9   246   | 1247   8     267   |
*---------------------------------------------------------*

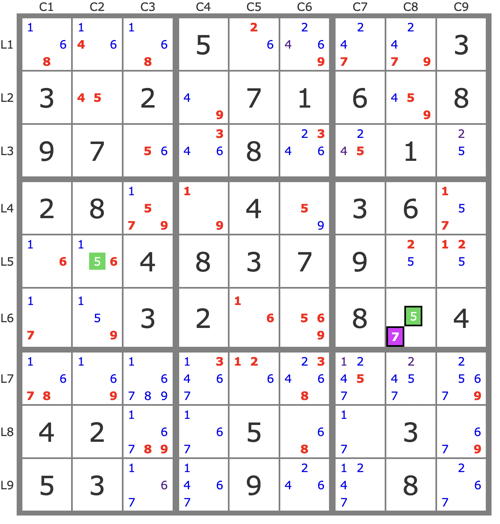
ALS XZ Rule: X = 7, Z = 1: (1=7) r6c1 - (7=1) r5c89, r6c8 => - 1 r5c12; stte

Leren

<Edit> Fixed typo. Thanks Mauries.

[Mauriès Robert]

Hi all,
Here is my two-step resolution with anti-tracks:

(-8r2c9)->8r2c1->3r3c3->5r2c2->25r5c89->... => -8r5c9 => r5c4=8 => 7 placements and basics.

puzzle1: Show

(-7r6c8)->5r6c8->5r5c2->... 5r2 empty => r6c8=7, stte.

puzzle1: Show

Robert

[P.O.]

thank you for your answers, my solution is also two steps:

Code: Select all

168     146     168     5       267     2469    2478    2479    3               
38      45      2       3479    37      1       6       4579    5789             
9       7       356     346     8       2346    245     1       25               
2       8      b13×5+79 139     4       359    b135-7   6      b15-7             
136    B1+56    4       1368    136     7       9      B2-5    B12-58             
1367    1569    135679  2       136     35689   13578  A5a7     4               
1678    169     16789   134678  12367   23468   12457   24579   125679           
4       2       16789   1678    5       68      17      3       1679             
5       3       167     1467    9       246     1247    8       1267


r6c8{n5n7} => r4c3 <> 5
||n5r6c8 - r5n5{c8c9 c2}
||n7r6c8 - r4n7{c7c9 c3}

Code: Select all

 168     146     168     5       267     2469    2478    2479    3               
B+38     45      2       3479    37      1       6       4579   A57+89             
 9       7      d×3+56   346     8       2346    245     1       25               
 2       8       1379    139     4       359     1357    6       157             
 136    c1+56    4       1368    136     7       9      b+25    a125+8             
 1367    1569   d13-5679 2       136     35689   13578   57      4               
 1678    169     16789   134678  12367   23468   12457   24579   125679           
 4       2       16789   1678    5       68      17      3       1679             
 5       3       167     1467    9       246     1247    8       1267


c9n8{r2r5} => r3c3 <> 3
||n8r2c9 - r2c1{n8 n3}
||n8r5c9 - r5n2{c9 c8} - r5n5{c8 c2} - c3n5{r6 r3}
ste.

[denis_berthier]

.
SER = 7.6

Code: Select all

Resolution state after Singles and whips[1]:
   +----------------------+----------------------+----------------------+
   ! 168    146    168    ! 5      267    2469   ! 2478   2479   3      !
   ! 38     45     2      ! 3479   37     1      ! 6      4579   5789   !
   ! 9      7      356    ! 346    8      2346   ! 245    1      25     !
   +----------------------+----------------------+----------------------+
   ! 2      8      13579  ! 139    4      359    ! 1357   6      157    !
   ! 136    156    4      ! 1368   136    7      ! 9      25     1258   !
   ! 1367   1569   135679 ! 2      136    35689  ! 13578  57     4      !
   +----------------------+----------------------+----------------------+
   ! 1678   169    16789  ! 134678 12367  23468  ! 12457  24579  125679 !
   ! 4      2      16789  ! 1678   5      68     ! 17     3      1679   !
   ! 5      3      167    ! 1467   9      246    ! 1247   8      1267   !
   +----------------------+----------------------+----------------------+
202 candidates.

Solvable in BC4: Show

biv-chain[3]: r2n8{c9 c1} - b1n3{r2c1 r3c3} - b1n5{r3c3 r2c2} ==> r2c9≠5
finned-x-wing-in-rows: n5{r2 r5}{c2 c8} ==> r6c8≠5
singles ==> r6c8=7, r4c3=7, r7c1=7
whip[1]: b7n8{r8c3 .} ==> r1c3≠8
whip[1]: b8n7{r9c4 .} ==> r2c4≠7
whip[1]: r4n9{c6 .} ==> r6c6≠9
naked-pairs-in-a-column: c3{r1 r9}{n1 n6} ==> r8c3≠6, r8c3≠1, r7c3≠6, r7c3≠1, r6c3≠6, r6c3≠1, r3c3≠6
whip[1]: r3n6{c6 .} ==> r1c5≠6, r1c6≠6
naked-pairs-in-a-block: b7{r7c3 r8c3}{n8 n9} ==> r7c2≠9
hidden-single-in-a-column ==> r6c2=9
hidden-pairs-in-a-block: b3{n7 n8}{r1c7 r2c9} ==> r2c9≠9, r1c7≠4, r1c7≠2
whip[1]: c9n9{r8 .} ==> r7c8≠9
naked-triplets-in-a-row: r2{c1 c5 c9}{n8 n3 n7} ==> r2c4≠3
finned-x-wing-in-rows: n3{r2 r5}{c1 c5} ==> r6c5≠3
biv-chain[3]: c2n4{r1 r2} - r2c4{n4 n9} - b3n9{r2c8 r1c8} ==> r1c8≠4
biv-chain[3]: r4c9{n1 n5} - c6n5{r4 r6} - r6n8{c6 c7} ==> r6c7≠1
biv-chain[3]: b2n6{r3c4 r3c6} - r8c6{n6 n8} - b5n8{r6c6 r5c4} ==> r5c4≠6
biv-chain[3]: c7n3{r4 r6} - r6c3{n3 n5} - b5n5{r6c6 r4c6} ==> r4c6≠3, r4c7≠5
biv-chain[4]: r3c9{n5 n2} - r1c8{n2 n9} - c6n9{r1 r4} - r4n5{c6 c9} ==> r7c9≠5, r5c9≠5
x-wing-in-rows: n5{r2 r5}{c2 c8} ==> r7c8≠5
hidden-single-in-a-block ==> r7c7=5
hidden-pairs-in-a-column: c7{n2 n4}{r3 r9} ==> r9c7≠7, r9c7≠1
naked-pairs-in-a-block: b9{r7c8 r9c7}{n2 n4} ==> r9c9≠2, r7c9≠2
biv-chain[3]: r4n3{c4 c7} - r6c7{n3 n8} - b5n8{r6c6 r5c4} ==> r5c4≠3
x-wing-in-rows: n3{r2 r5}{c1 c5} ==> r7c5≠3, r6c1≠3
naked-pairs-in-a-row: r6{c1 c5}{n1 n6} ==> r6c6≠6
whip[1]: b5n6{r6c5 .} ==> r7c5≠6
biv-chain[3]: r5n3{c1 c5} - c5n6{r5 r6} - r6n1{c5 c1} ==> r5c1≠1
biv-chain[4]: c7n3{r4 r6} - r6c3{n3 n5} - r5n5{c2 c8} - r4c9{n5 n1} ==> r4c7≠1
stte

No 1-step solution in W8, but many 2-step solutions with reversible chains only, in Z5:

1st step: z-chain[5]: r5n2{c9 c8} - r5n5{c8 c2} - b1n5{r2c2 r3c3} - b1n3{r3c3 r2c1} - r2n8{c1 .} ==> r5c9≠8
singles ==> r6c7=8, r2c9=8, r2c1=3, r2c5=7, r5c4=8, r5c5=3, r6c3=3, r4c7=3
whip[1]: c7n1{r9 .} ==> r7c9≠1, r8c9≠1, r9c9≠1
whip[1]: b5n6{r6c6 .} ==> r6c1≠6, r6c2≠6
whip[1]: c9n9{r8 .} ==> r7c8≠9

2nd step: a lot of possible bivalue-chains[4]:
biv-chain[4]: b3n9{r1c8 r2c8} - r2n5{c8 c2} - c3n5{r3 r4} - r4c6{n5 n9} ==> r1c6≠9
stte
or
biv-chain[4]: b2n9{r2c4 r1c6} - r4c6{n9 n5} - c3n5{r4 r3} - r2c2{n5 n4} ==> r2c4≠4
stte
or
biv-chain[4]: r2n5{c8 c2} - c3n5{r3 r4} - r4c6{n5 n9} - b2n9{r1c6 r2c4} ==> r2c8≠9
stte
or
biv-chain[4]: r2n9{c4 c8} - r2n5{c8 c2} - c3n5{r3 r4} - r4c6{n5 n9} ==> r4c4≠9, r1c6≠9
stte