The New Sudoku Players' Forum

by **P.O.** » Thu Mar 10, 2022 6:49 pm

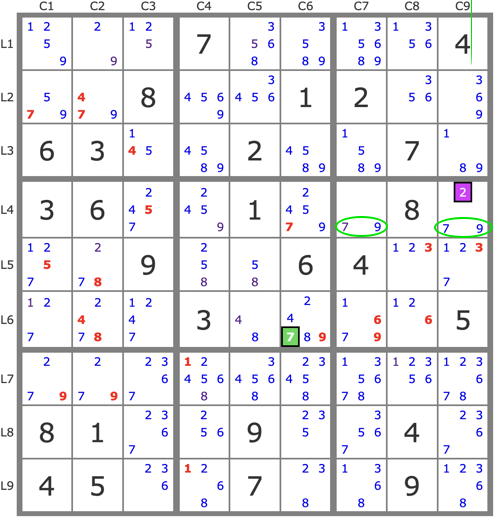
Code: Select all: . . . 7 . . . . 4 . . 8 . . 1 2 . . 6 3 . . 2 . . 7 . 3 6 . . 1 . . 8 . . . 9 . . 6 4 . . . . . 3 . . . . 5 . . . . . . . . . 8 1 . . 9 . . 4 . 4 5 . . 7 . . 9 . ...7....4..8..12..63..2..7.36..1..8...9..64.....3....5.........81..9..4.45..7..9.

by **yzfwsf** » Thu Mar 10, 2022 7:41 pm

ALS Continuous Nice Loop: 7r5c9 = r5c12 - r46c3 = r78c3 - (7=92)r7c12 - r7c8 = r56c8 - (2=97)r4c79 => r7c3469,r5c9<>2,r6c127<>7,r4c46,r6c7<>9
stte

by **Mauriès Robert** » Thu Mar 10, 2022 8:31 pm

Hi all,
An immediate resolution is as follows:
(-2r4c9)->79r4c79->7r6c6->... 9b5 empty => r4c9=2, btte.

puzzle: Show

Robert

by **rjamil** » Thu Mar 10, 2022 8:37 pm

Code: Select all: +------------------+------------------------+-----------------------+ | 1259 29 125 | 7 3568 3589 | 135689 1356 4 | | 579 479 8 | 4569 3456 1 | 2 356 369 | | 6 3 145 | 4589 2 4589 | 1589 7 189 | +------------------+------------------------+-----------------------+ | 3 6 245-7| 245(9) 1 245(79) | (79) 8 2-79 | | 1257 278 9 | 258 58 6 | 4 123 1237 | | 127 2478 1247 | 3 48 (79)-248| 1679 126 5 | +------------------+------------------------+-----------------------+ | 279 279 2367 | 124568 34568 23458 | 135678 12356 123678 | | 8 1 2367 | 256 9 235 | 3567 4 2367 | | 4 5 236 | 1268 7 238 | 1368 9 12368 | +------------------+------------------------+-----------------------+

Almost Locked Pair: 79 @ r4c46 r4c7 r6c6 => -7 @ r4c3 => -79 @ r4c9 => -248 @ r6c6; btte

R. Jamil

Website · by **denis_berthier** » Fri Mar 11, 2022 5:43 am

.
SER = 7.0

Code: Select all: Resolution state after Singles (and whips[1]): +----------------------+----------------------+----------------------+ ! 1259 29 125 ! 7 3568 3589 ! 135689 1356 4 ! ! 579 479 8 ! 4569 3456 1 ! 2 356 369 ! ! 6 3 145 ! 4589 2 4589 ! 1589 7 189 ! +----------------------+----------------------+----------------------+ ! 3 6 2457 ! 2459 1 24579 ! 79 8 279 ! ! 1257 278 9 ! 258 58 6 ! 4 123 1237 ! ! 127 2478 1247 ! 3 48 24789 ! 1679 126 5 ! +----------------------+----------------------+----------------------+ ! 279 279 2367 ! 124568 34568 23458 ! 135678 12356 123678 ! ! 8 1 2367 ! 256 9 235 ! 3567 4 2367 ! ! 4 5 236 ! 1268 7 238 ! 1368 9 12368 ! +----------------------+----------------------+----------------------+ 207 candidates

There is a totally elementary solution using only bivalue-chains[3]:

Code: Select all: biv-chain[3]: r4c7{n7 n9} - r6n9{c7 c6} - b5n7{r6c6 r4c6} ==> r4c3≠7, r4c9≠7 biv-chain[3]: r4c9{n2 n9} - r6n9{c7 c6} - b5n7{r6c6 r4c6} ==> r4c6≠2 biv-chain[3]: r4c7{n9 n7} - b5n7{r4c6 r6c6} - r6n9{c6 c7} ==> r1c7≠9, r3c7≠9, r4c9≠9 singles ==> r4c9=2, r7c8=2 whip[1]: b7n2{r9c3 .} ==> r1c3≠2, r6c3≠2 whip[1]: b9n5{r8c7 .} ==> r1c7≠5, r3c7≠5 naked-pairs-in-a-block: b7{r7c1 r7c2}{n7 n9} ==> r8c3≠7, r7c3≠7 stte

I've a 1-step solution, but it's in B9, absurd for a puzzle in BC3:

Code: Select all: braid[9]: b4n5{r4c3 r5c1} - r5c5{n5 n8} - r5c4{n8 n2} - r4n2{c6 c9} - c8n2{r6 r7} - r5c2{n2 n7} - r2n7{c2 c1} - r7c1{n2 n9} - r7c2{n9 .} ==> r4c3≠4 w1-tte

by **P.O.** » Sat Mar 12, 2022 8:30 am

thank you for your answers, here is my solution:

Code: Select all: / - r4c7{n7 n9} 》r4c4 r4c6 r6c7 <> 9 / - {r4r6} - r5n7{c1c2 c9} 》r6c7 <> 7 c3n7 \ - {r7r8} - r7{c1c2}{n2n9} - c8n2{r7 r5r6} - r4{c7c9}{n7n9} singles + intersection ste.

by **pjb** » Sat Mar 12, 2022 9:38 pm

Although only a btte solution, I like it's simplicity:

Code: Select all: 1259 29 125 | 7 3568 3589 | 13568-9 1356 4 579 479 8 | 4569 3456 1 | 2 356 369 6 3 145 | 4589 2 4589 | 158-9 7 189 ------------------------+----------------------+--------------------- 3 6 245-7 | 2459 1 d24579 |a79 8 2-79 1257 278 9 | 258 58 6 | 4 123 1237 127 2478 1247 | 3 48 c79-248 |b1679 126 5 ------------------------+----------------------+--------------------- 279 279 2367 | 124568 34568 23458 | 135678 12356 123678 8 1 2367 | 256 9 235 | 3567 4 2367 4 5 236 | 1268 7 238 | 1368 9 12368

Continuous loop: (7=9)r4c7 - (9)r6c7 = (9-7)r6c6 = (7)r4c6 - loop => -9 r13c7; -79 r4c9; -7 r4c3; -248 r6c6; btte

Phil

Puzzle 25