- Code: Select all
. . . 6 . . . . 9
8 6 . . 4 . . 7 .
. . . . . 3 5 . .
6 3 . . 1 . . 4 .
. . . . . . . . .
2 4 . . 8 . . 3 .
4 9 . . 2 . . 5 .
. . . . . 1 2 . .
. . . 7 . . . . 8
...6....986..4..7......35..63..1..4..........24..8..3.49..2..5......12.....7....8
Puzzle 24
11 posts
• Page 1 of 1
Re: Puzzle 24
I found a solution with two chains (I did not search further for a one-stepper).
1. Loop (6)r5c5 = (6)r56c6 - (6=83)r7c46 - r5c4 = (3-6)r5c5
=> -6 r9c6, -8 r7c3, -3 r8c4, -579 r5c5 [& 2 LC eliminations]
---
2. (8)r3c4 = (8-34)r75c4 = (4)r8c4 - r9c6 = r9c7 - r8c9 = (4-6)r3c9 = (6)r3c8 => -8 r7c8; ste
Thanks for the puzzle!
- Code: Select all
.-----------------------------------------------------------------------------.
| 1357 1257 123457 | 6 57 2578 | 1348 128 9 |
| 8 6 12359 | 1259 4 259 | 13 7 123 |
| 179 127 12479 | 1289 79 3 | 5 1268 1246 |
|-------------------------+-------------------------+-------------------------|
| 6 3 5789 | 259 1 2579 | 789 4 257 |
| 1579 1578 15789 |d23459 ea36-579 b245679 | 16789 12689 12567 |
| 2 4 1579 | 59 8 b5679 | 1679 3 1567 |
|-------------------------+-------------------------+-------------------------|
| 4 9 1367-8 |c38 2 c68 | 1367 5 1367 |
| 357 578 35678 | 4589-3 3569 1 | 2 69 3467 |
| 135 125 12356 | 7 3569 459-6 | 13469 169 8 |
'-----------------------------------------------------------------------------'
1. Loop (6)r5c5 = (6)r56c6 - (6=83)r7c46 - r5c4 = (3-6)r5c5
=> -6 r9c6, -8 r7c3, -3 r8c4, -579 r5c5 [& 2 LC eliminations]
---
- Code: Select all
.-----------------------------------------------------------------------------.
| 1357 1257 123457 | 6 57 258 | 1348 128 9 |
| 8 6 12359 | 1259 4 259 | 13 7 123 |
| 179 127 12479 |a1289 79 3 | 5 h126-8 g1246 |
|-------------------------+-------------------------+-------------------------|
| 6 3 5789 | 259 1 2579 | 789 4 257 |
| 1579 1578 15789 |b23459 36 245679 | 16789 12689 12567 |
| 2 4 1579 | 59 8 5679 | 1679 3 1567 |
|-------------------------+-------------------------+-------------------------|
| 4 9 1367 |b38 2 68 | 1367 5 1367 |
| 357 578 35678 |c459 3569 1 | 2 69 f3467 |
| 135 125 12356 | 7 3569 d459 |e13469 169 8 |
'-----------------------------------------------------------------------------'
2. (8)r3c4 = (8-34)r75c4 = (4)r8c4 - r9c6 = r9c7 - r8c9 = (4-6)r3c9 = (6)r3c8 => -8 r7c8; ste
Thanks for the puzzle!
JCO
- jco
- Posts: 893
- Joined: 09 June 2020
Re: Puzzle 24
- Code: Select all
1357 1257 123457 | 6 57 2578 | 1348 128 9
8 6 12359 | 1259 4 259 | 13 7 123
179 127 12479 |g1289 79 3 | 5 f1268 e1246
------------------------+-----------------------+---------------------
6 3 5789 | 259 1 2579 | 789 4 257
1579 1578 15789 |b2459-3 a35679 245679 | 16789 12689 12567
2 4 1579 | 59 8 5679 | 1679 3 1567
------------------------+-----------------------+---------------------
4 9 13678 |h38 2 68 | 1367 5 1367
357 578 35678 |c34589 569-3 1 | 2 69 d3467
135 125 12356 | 7 569-3 4569 | 13469 169 8
(3)r5c5 = (3-4)r5c4 = (4)r8c4 - (4)r8c9 = (4-6)r3c9 = (6-8)r3c8 = (8)r3c4 - (8=3)r7c4 => -3 r5c4, r89c5; btte
or better
(8)r3c4 = (8-6)r3c8 = (6-4)r3c9 = (4)r8c9 - (4)r8c4 = (4-3)r5c4 = (3-6)r5c5 = (6)r89c5 - (6=8)r7c6 => -8 r1c6, r78c4; stte
Thanks, Phil
- pjb
- 2014 Supporter
- Posts: 2749
- Joined: 11 September 2011
- Location: Sydney, Australia
Re: Puzzle 24
- Code: Select all
+------------------+---------------------+-------------------+
| 1357 1257 123457 | 6 57 257-8 |a1348 a128 9 |
| 8 6 12359 | 1259 4 259 |a13 7 a123 |
| 179 127 12479 | 1289 79 3 | 5 1268 1246 |
+------------------+---------------------+-------------------+
| 6 3 5789 |d259 1 d2579 | 789 4 257 |
| 1579 1578 15789 | 23459 35679 d245679 | 16789 12689 12567 |
| 2 4 1579 |d59 8 d5679 | 1679 3 1567 |
+------------------+---------------------+-------------------+
| 4 9 13678 | 38 2 e68 | 1367 5 1367 |
| 357 578 35678 | 34589 3569 1 | 2 69 3467 |
| 135 125 12356 | 7 3569 c4569 |b13469 169 8 |
+------------------+---------------------+-------------------+
(8=1234)b3p1246 - (4)r9c7 = (4)r9c6 - (4=25796)b5p13679 - (6=8)r7c6 => -8r1c6; stte
- RSW
- Posts: 706
- Joined: 01 December 2018
- Location: Western Canada
Re: Puzzle 24
.
SER = 7.3
The simplest-first solution, in W4, involves many elimination steps.
Notice that:
- the number of candidates after whips[1] is very large for a puzzle in W4 (more than 3 standard deviations above the mean, see http://forum.enjoysudoku.com/relation-between-difficulty-and-number-of-candidates-t39836-1.html);
- there is not a single Single before all these eliminations.
Surprisingly, there is a 1-step solution in BC5:
SER = 7.3
- Code: Select all
Resolution state after Singles (and whips[1]):
+----------------------+----------------------+----------------------+
! 1357 1257 123457 ! 6 57 2578 ! 1348 128 9 !
! 8 6 12359 ! 1259 4 259 ! 13 7 123 !
! 179 127 12479 ! 1289 79 3 ! 5 1268 1246 !
+----------------------+----------------------+----------------------+
! 6 3 5789 ! 259 1 2579 ! 789 4 257 !
! 1579 1578 15789 ! 23459 35679 245679 ! 16789 12689 12567 !
! 2 4 1579 ! 59 8 5679 ! 1679 3 1567 !
+----------------------+----------------------+----------------------+
! 4 9 13678 ! 38 2 68 ! 1367 5 1367 !
! 357 578 35678 ! 34589 3569 1 ! 2 69 3467 !
! 135 125 12356 ! 7 3569 4569 ! 13469 169 8 !
+----------------------+----------------------+----------------------+
218 candidates
The simplest-first solution, in W4, involves many elimination steps.
Notice that:
- the number of candidates after whips[1] is very large for a puzzle in W4 (more than 3 standard deviations above the mean, see http://forum.enjoysudoku.com/relation-between-difficulty-and-number-of-candidates-t39836-1.html);
- there is not a single Single before all these eliminations.
- Code: Select all
z-chain[4]: b2n8{r1c6 r3c4} - r7c4{n8 n3} - r5n3{c4 c5} - c5n7{r5 .} ==> r1c6≠7
whip[1]: c6n7{r6 .} ==> r5c5≠7
z-chain[4]: r7c6{n6 n8} - r7c4{n8 n3} - r5n3{c4 c5} - c5n6{r5 .} ==> r9c6≠6
t-whip[4]: r7c6{n8 n6} - c5n6{r9 r5} - r5n3{c5 c4} - r7c4{n3 .} ==> r7c3≠8, r8c4≠8
t-whip[4]: r7c4{n3 n8} - r7c6{n8 n6} - c5n6{r9 r5} - r5n3{c5 .} ==> r8c4≠3
t-whip[4]: b9n4{r9c7 r8c9} - c4n4{r8 r5} - c4n3{r5 r7} - b9n3{r7c7 .} ==> r9c7≠1, r9c7≠6, r9c7≠9
whip[1]: b9n9{r9c8 .} ==> r5c8≠9
biv-chain[3]: r2c7{n1 n3} - r9c7{n3 n4} - b3n4{r1c7 r3c9} ==> r3c9≠1
biv-chain[4]: r3n6{c8 c9} - b3n4{r3c9 r1c7} - r9c7{n4 n3} - r2c7{n3 n1} ==> r3c8≠1
t-whip[4]: r5n3{c5 c4} - r7c4{n3 n8} - r7c6{n8 n6} - c5n6{r9 .} ==> r5c5≠5, r5c5≠9
t-whip[4]: r3n8{c8 c4} - c4n1{r3 r2} - r2c7{n1 n3} - r2c9{n3 .} ==> r3c8≠2
biv-chain[4]: r3c8{n6 n8} - c4n8{r3 r7} - c4n3{r7 r5} - r5c5{n3 n6} ==> r5c8≠6
whip[4]: r1c5{n5 n7} - r3c5{n7 n9} - r2n9{c6 c3} - r2n5{c3 .} ==> r1c6≠5
biv-chain[3]: c8n2{r5 r1} - r1c6{n2 n8} - r3n8{c4 c8} ==> r5c8≠8
whip[1]: c8n8{r3 .} ==> r1c7≠8
naked-triplets-in-a-column: c7{r1 r2 r9}{n4 n1 n3} ==> r7c7≠3, r7c7≠1, r6c7≠1, r5c7≠1
whip[1]: c7n1{r2 .} ==> r1c8≠1, r2c9≠1
naked-pairs-in-a-row: r1{c6 c8}{n2 n8} ==> r1c3≠2, r1c2≠2
x-wing-in-rows: n1{r6 r7}{c3 c9} ==> r9c3≠1, r5c9≠1, r5c3≠1, r3c3≠1, r2c3≠1, r1c3≠1
biv-chain[4]: c4n3{r5 r7} - c4n8{r7 r3} - r1c6{n8 n2} - c8n2{r1 r5} ==> r5c4≠2
biv-chain[4]: r1c6{n2 n8} - r7n8{c6 c4} - c4n3{r7 r5} - b5n4{r5c4 r5c6} ==> r5c6≠2
whip[1]: r5n2{c9 .} ==> r4c9≠2
biv-chain[4]: b3n6{r3c9 r3c8} - c8n8{r3 r1} - c8n2{r1 r5} - b6n1{r5c8 r6c9} ==> r6c9≠6
biv-chain[4]: c4n1{r3 r2} - r2c7{n1 n3} - r2c9{n3 n2} - r1n2{c8 c6} ==> r3c4≠2
biv-chain[4]: r7c4{n3 n8} - b2n8{r3c4 r1c6} - r1c8{n8 n2} - r2c9{n2 n3} ==> r7c9≠3
hidden-pairs-in-a-block: b9{n3 n4}{r8c9 r9c7} ==> r8c9≠7, r8c9≠6
whip[1]: r8n7{c3 .} ==> r7c3≠7
biv-chain[3]: r8c9{n3 n4} - c4n4{r8 r5} - c4n3{r5 r7} ==> r8c5≠3
biv-chain[4]: b8n3{r9c5 r7c4} - c4n8{r7 r3} - c4n1{r3 r2} - r2c7{n1 n3} ==> r9c7≠3
stte
Surprisingly, there is a 1-step solution in BC5:
- Code: Select all
biv-chain[5]: r7c4{n3 n8} - r3n8{c4 c8} - b3n6{r3c8 r3c9} - c9n4{r3 r8} - c4n4{r8 r5} ==> r5c4≠3
w1-tte
- denis_berthier
- 2010 Supporter
- Posts: 4665
- Joined: 19 June 2007
- Location: Paris
Re: Puzzle 24
Hi all,
Another one-step resolution is as follows (with an anti-track):
(-4r3c9)->4r8c9->[ 4r5c4->3r5c5->6r56c6->8r7c6->3r7c4 ]->3r2c9->1r2c7->1r3c4->... => 8c4 empty => r3c9=4, stte.
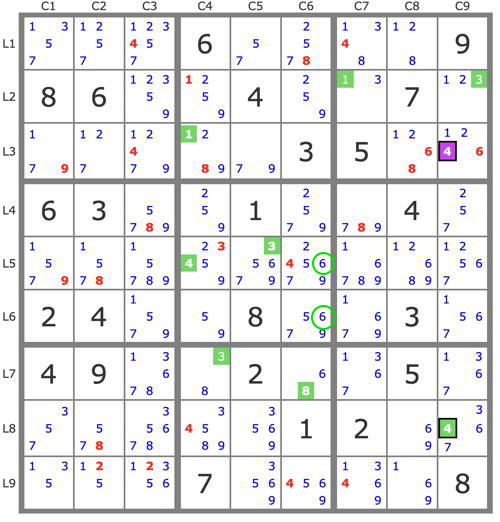
Robert
Another one-step resolution is as follows (with an anti-track):
(-4r3c9)->4r8c9->[ 4r5c4->3r5c5->6r56c6->8r7c6->3r7c4 ]->3r2c9->1r2c7->1r3c4->... => 8c4 empty => r3c9=4, stte.

Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: Puzzle 24
thank you for your answers;
i always find it interesting to read the somewhat complicated solutions; while some can be called classics in a way, some, especially those involving large sets of candidates like those of RSW, are very surprising;
my solution is to expand both legs of a xor relationship:
i always find it interesting to read the somewhat complicated solutions; while some can be called classics in a way, some, especially those involving large sets of candidates like those of RSW, are very surprising;
my solution is to expand both legs of a xor relationship:
- Code: Select all
1357 1257 123457 6 57 2578 1348 128 9
8 6 12359 1259 4 259 13 7 123
179 127 12479 B12+89 79 3 5 A12+68 a124+6
6 3 5789 259 1 2579 789 4 257
1579 1578 15789 c2×3+459 35679 245679 16789 12689 12567
2 4 1579 59 8 5679 1679 3 1567
4 9 13678 C+38 2 68 1367 5 1367
357 578 35678 c3-4589 3569 1 2 69 b3+467
135 125 12356 7 3569 4569 13469 169 8
/ c8 - r3n8{c8 c4} - r7c4{n8 n3}
r3n6 》r5c4 <> 3
\ c9 - c9n4{r3 r8} - c4n4{r8 r5}
single: n3r5c5
intersection: c6n6{r5r6} => r7c6 r9c6 <> 6
ste.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 24
P.O. wrote:those involving large sets of candidates like those of RSW, are very surprising
I don't deliberately try to find large subsets, but that's the way it works out sometimes. My primary goal is to find a one step solution using the shortest/simplest AIC possible, but the shortest is not necessarily the simplest, and the simplest is not necessarily the shortest. So, it's a bit of a compromise and a somewhat subjective decision as to what is the best solution.
Thank you for posting these puzzles.
- RSW
- Posts: 706
- Joined: 01 December 2018
- Location: Western Canada
Re: Puzzle 24
P.O. wrote:
- Code: Select all
/ c8 - r3n8{c8 c4} - r7c4{n8 n3}
r3n6 》r5c4 <> 3
\ c9 - c9n4{r3 r8} - c4n4{r8 r5}
This is a network presentation of the bivalue-chain in my answer.
- denis_berthier
- 2010 Supporter
- Posts: 4665
- Joined: 19 June 2007
- Location: Paris
Re: Puzzle 24
hi Denis,
a chain start by a xor relationship between two candidates (A,B) then only one leg is developed A<--XOR-->B-->(bi...) each (bi) tested against (A) for elimination; i am experimenting developing both legs (ai...)<--A<--XOR-->B-->(bi...) and comparing both sets of links (ai,bi); this is the way it was found:
I have also a bivalue-chain: c4n4{r5 r8} - c9n4{r8 r3} - r3n6{c9 c8} - r3n8{c8 c4} - r7c4{n8 n3} => r5c4 <> 3
a chain start by a xor relationship between two candidates (A,B) then only one leg is developed A<--XOR-->B-->(bi...) each (bi) tested against (A) for elimination; i am experimenting developing both legs (ai...)<--A<--XOR-->B-->(bi...) and comparing both sets of links (ai,bi); this is the way it was found:
- Code: Select all
Roots: (((6 0) (3 8 3) (1 2 6 8)) ((6 0) (3 9 3) (1 2 4 6)))
Elimination: ((((5 4 5) (2 3 4 5 9))) (3))
((6 0) (3 8 3) (1 2 6 8))
((8 1 10) (3 4 2) (1 2 8 9))
((3 2 9) (7 4 8) (3 8))
((6 0) (3 9 3) (1 2 4 6))
((4 1 10) (8 9 9) (3 4 6 7))
((4 2 1) (5 4 5) (2 3 4 5 9))
I have also a bivalue-chain: c4n4{r5 r8} - c9n4{r8 r3} - r3n6{c9 c8} - r3n8{c8 c4} - r7c4{n8 n3} => r5c4 <> 3
- Code: Select all
depth: 4 candidate: 3 from start
((4 0) (5 4 5) (2 3 4 5 9)) A -||||
((4 0) (8 4 8) (3 4 5 8 9)) B ||||
((4 1 1) (3 9 3) (1 2 4 6)) b1 -||||
((6 2 10) (3 8 3) (1 2 6 8)) b2 --||| } nothing
((8 3 10) (3 4 2) (1 2 8 9)) b3 ---||
((3 4 9) (7 4 8) (3 8)) b4 ----| elimination found.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 24
Hi P.O.
Yes, I understand. But in the present case, the network presentation is more complicated.
Yes, I understand. But in the present case, the network presentation is more complicated.
- denis_berthier
- 2010 Supporter
- Posts: 4665
- Joined: 19 June 2007
- Location: Paris
11 posts
• Page 1 of 1

