- Code: Select all
this one is maybe a bit more difficult:
. . . 1 4 . . 6 .
. . 8 . . . . . 1
6 . . 7 8 . . . .
. . 2 3 . . . 1 .
8 . . . . 7 . . 5
. 6 . . . . 2 . .
. 3 . . . . 9 . .
. . 6 . . 4 . 5 .
4 . . . 9 . . . 7
...14..6...8.....16..78......23...1.8....7..5.6....2...3....9....6..4.5.4...9...7
Puzzle 23
6 posts
• Page 1 of 1
Puzzle 23
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 23
- Code: Select all
+--------------------+---------------------+-----------------+
| 23579 2579 3579 | 1 4 2359 | 3578 6 2389 |
| 23579 24579 8 | 2569 2356 23569 | 3457 23479 1 |
| 6 12459 13459 | 7 8 2359 | 345 2349 2349 |
+--------------------+---------------------+-----------------+
| 579 4579 2 | 3 56 5689 | 4678 1 b4689 |
| 8 a149 a1349 |f2469 g26-1 7 |a346 a349 5 |
| 13579 6 134579 | 4589 15 1589 | 2 34789 3489 |
+--------------------+---------------------+-----------------+
|d1257 3 d157 |d2568 d12567 d12568 | 9 248 c2468 |
| 1279 12789 6 |e28 1237 4 | 138 5 238 |
| 4 1258 15 | 2568 9 123568 | 1368 238 7 |
+--------------------+---------------------+-----------------+
(1=3496)r5c2378 - (6)r4c9 = (6)r7c9 - (6=12578)r7c13456 - (8=2)r8c4 - (2)r5c4 = (2)r5c5 => -1r5c5; btte
Thanks for the puzzle.
- RSW
- Posts: 706
- Joined: 01 December 2018
- Location: Western Canada
Re: Puzzle 23
- Code: Select all
my solution:
an ordinary chain that expands a single branch of the xor relationship between n2 in r5:
23579 2579 3579 1 4 2359 3578 6 2389
23579 24579 8 2569 2356 23569 3457 23479 1
6 12459 13459 7 8 2359 345 2349 2349
579 4579 2 3 56 5689 4678 1 4689
8 149 1349 a+2469 fa×1±2+6 7 f34-6 349 5
13579 6 134579 4589 15 1589 2 34789 3489
1257 3 157 c256-8 12567 c1256-8 9 c24*8 c246*8
1279 12789 6 b2+8 1237 4 e(1)38 5 d(23)8
4 1258 15 2568 9 123568 e(16)38 d(23)8 7
r5n2{c5 c4} - r8c4{n2 n8} - r7n8{c4c6 c8c9} - b9{r8c9r9c8}{n2n3} - c7{r8r9}{n1n6} - r5n6{c7 c5} => r5c5 <> 1
or expanding the two branches of the xor relationship between n6 in c9:
23579 2579 3579 1 4 2359 3578 6 2389
23579 24579 8 2569 2356 23569 3457 23479 1
6 12459 13459 7 8 2359 345 2349 2349
579 4579 2 3 B+56 5689 4678 1 A4+689
8 149 1349 e-2469 e×1+26 7 346 349 5
13579 6 134579 4589 C+15 1589 2 34789 3489
1257 3 157 c256*8 12567 c1256*8 9 b2+48 a24+68
1279 12789 6 d+28 1237 4 138 5 238
4 1258 15 2568 9 123568 1368 238 7
/- r4 - r4c5{n6 n5} - r6c5{n5 n1}
n6c9 => r5c5 <> 1
\- r7 - r7n4{c9 c8} - r7n8{c8 c4c6} - r8c4{n8 n2} - r5n2{c4 c5}
then:
intersections : r6n1{c5c6} => r6c1 r6c3 <> 1
c1n1{r7r8} => r7c3 r8c2 r9c2 r9c3 <> 1
ste.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 23
Hi all,
To make it different, here is another possible resolution:
(-6r5c7)->26r5c45->1r6c56->{ [ (1r78c1->5r9c3)->28r9c2 ]->7r7c3->7r8c5->3r9c6->28r9c8 }->6r9c4->... => -6r9c7, btte
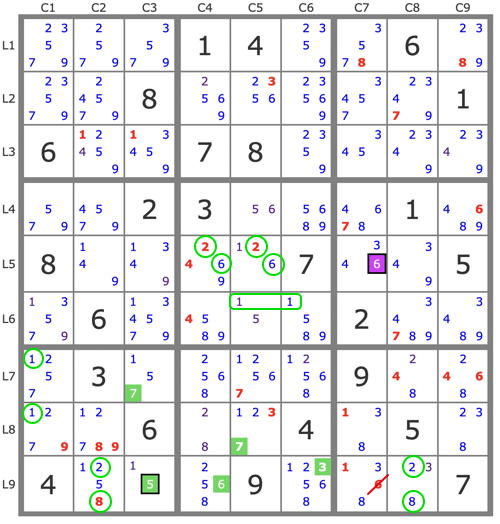
Robert
To make it different, here is another possible resolution:
(-6r5c7)->26r5c45->1r6c56->{ [ (1r78c1->5r9c3)->28r9c2 ]->7r7c3->7r8c5->3r9c6->28r9c8 }->6r9c4->... => -6r9c7, btte

Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: Puzzle 23
hi Robert,
it's a really interesting chain, very good find.
it's a really interesting chain, very good find.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 23
.
SER = 8.6
1) Simplest-first solution in W5:
2) 2-step solutions, in W5:
SER = 8.6
- Code: Select all
Resolution state after Singles (and whips[1]):
+----------------------+----------------------+----------------------+
! 23579 2579 3579 ! 1 4 2359 ! 3578 6 2389 !
! 23579 24579 8 ! 2569 2356 23569 ! 3457 23479 1 !
! 6 12459 13459 ! 7 8 2359 ! 345 2349 2349 !
+----------------------+----------------------+----------------------+
! 579 4579 2 ! 3 56 5689 ! 4678 1 4689 !
! 8 149 1349 ! 2469 126 7 ! 346 349 5 !
! 13579 6 134579 ! 4589 15 1589 ! 2 34789 3489 !
+----------------------+----------------------+----------------------+
! 1257 3 157 ! 2568 12567 12568 ! 9 248 2468 !
! 1279 12789 6 ! 28 1237 4 ! 138 5 238 !
! 4 1258 15 ! 2568 9 123568 ! 1368 238 7 !
+----------------------+----------------------+----------------------+
225 candidates
1) Simplest-first solution in W5:
- Code: Select all
t-whip[3]: r9c3{n5 n1} - c1n1{r8 r6} - r6c5{n1 .} ==> r6c3≠5
t-whip[4]: c2n8{r9 r8} - r8c4{n8 n2} - r8c9{n2 n3} - r9n3{c8 .} ==> r9c6≠8
z-chain[5]: c2n8{r9 r8} - r8c4{n8 n2} - r5n2{c4 c5} - r5n1{c5 c3} - r3n1{c3 .} ==> r9c2≠1
t-whip[5]: c4n4{r6 r5} - r5n2{c4 c5} - r5n6{c5 c7} - c9n6{r4 r7} - r7n4{c9 .} ==> r6c8≠4
whip[5]: r9c3{n1 n5} - r7c3{n5 n7} - r8n7{c2 c5} - b8n1{r8c5 r9c6} - b8n3{r9c6 .} ==> r7c1≠1
finned-x-wing-in-columns: n1{c1 c6}{r6 r8} ==> r8c5≠1
biv-chain[5]: c9n6{r7 r4} - r4c5{n6 n5} - r6c5{n5 n1} - c1n1{r6 r8} - b9n1{r8c7 r9c7} ==> r9c7≠6
stte
2) 2-step solutions, in W5:
- Code: Select all
1st step:
whip[5]: r9c3{n1 n5} - r7c3{n5 n7} - r8n7{c2 c5} - b8n3{r8c5 r9c6} - b8n1{r9c6 .} ==> r7c1≠1
2nd step:
biv-chain[5]: b9n6{r7c9 r9c7} - c7n1{r9 r8} - c1n1{r8 r6} - r6c5{n1 n5} - r4c5{n5 n6} ==> r4c9≠6, r7c5≠6
OR:
biv-chain[5]: c9n6{r7 r4} - r4c5{n6 n5} - r6c5{n5 n1} - c1n1{r6 r8} - b9n1{r8c7 r9c7} ==> r9c7≠6
w1-tte
- denis_berthier
- 2010 Supporter
- Posts: 4665
- Joined: 19 June 2007
- Location: Paris
6 posts
• Page 1 of 1

