- Code: Select all
9 . . . . 6 2 . .
. . 1 . 8 . . . .
. 5 . 3 . . . . 9
7 . . . . . 6 9 .
. 1 . . . 8 . . .
. . . 4 . . 8 1 .
3 . . . . 4 . . 6
. . 4 . 9 . . . .
. 7 . 2 . . . 5 .
9....62....1.8.....5.3....97.....69..1...8......4..81.3....4..6..4.9.....7.2...5.
Puzzle 21
5 posts
• Page 1 of 1
Re: Puzzle 21
- Code: Select all
.-----------------------------------------------------------------------------.
| 9 348 378 | 157 1457 6 | 2 3478 134578 |
| 246 2346 1 | 579 8 2579 | 3457 3467 3457 |
| 2468 5 2678 | 3 1247 127 | 147 4678 9 |
|-------------------------+-------------------------+-------------------------|
| 7 2348 2358 | 15 1235 1235 | 6 9 2345 |
| 2456 1 c23569 |d5679 23567 8 | 3457 2347 23457 |
| 256 b2369 23569 | 4 23567 23579 | 8 1 2357 |
|-------------------------+-------------------------+-------------------------|
| 3 a289 2589 |g1578 g157 4 |h17-9 278 6 |
| 12568 268 4 |e15678 9 1357 | 137 2378 12378 |
| 168 7 689 | 2 f136 f13 | 1349 5 1348 |
'-----------------------------------------------------------------------------'
1. (9)r7c2 = (9)r6c2 - (9)r5c3 = (9-6)r5c4 = (6)r8c4 - (6=31)r9c56 - (1)r7c45 = (1)r7c7 => -9 r7c7; ste
Thanks for the puzzle!
JCO
- jco
- Posts: 893
- Joined: 09 June 2020
Re: Puzzle 21
i have the same 1 step solution as JCO so these 2 steps plus basics:
r4n8{c3 c2} - r4n4{c2 c9} - r9n4{c9 c7} - r9n9{c7 c3} => r9c3 <> 8
r5n9{c4 c3} - r9c3{n9 n6} - b8n6{r9c5 r8c4} => r5c4 <> 6
then singles + basics
ste.
r4n8{c3 c2} - r4n4{c2 c9} - r9n4{c9 c7} - r9n9{c7 c3} => r9c3 <> 8
r5n9{c4 c3} - r9c3{n9 n6} - b8n6{r9c5 r8c4} => r5c4 <> 6
then singles + basics
ste.
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 21
.
First, note there's an elementary solution in W4:
The simplest 1-step whip solution requires a whip[7]:
Absurd for a puzzle on the very easy side of W4
- Code: Select all
Resolution state after Singles and whips[1]:
+----------------------+----------------------+----------------------+
! 9 348 378 ! 157 1457 6 ! 2 3478 134578 !
! 246 2346 1 ! 579 8 2579 ! 3457 3467 3457 !
! 2468 5 2678 ! 3 1247 127 ! 147 4678 9 !
+----------------------+----------------------+----------------------+
! 7 2348 2358 ! 15 1235 1235 ! 6 9 2345 !
! 2456 1 23569 ! 5679 23567 8 ! 3457 2347 23457 !
! 256 2369 23569 ! 4 23567 23579 ! 8 1 2357 !
+----------------------+----------------------+----------------------+
! 3 289 2589 ! 1578 157 4 ! 179 278 6 !
! 12568 268 4 ! 15678 9 1357 ! 137 2378 12378 !
! 168 7 689 ! 2 136 13 ! 1349 5 1348 !
+----------------------+----------------------+----------------------+
218 candidates
First, note there's an elementary solution in W4:
- Code: Select all
t-whip[3]: r9c6{n3 n1} - r7n1{c5 c7} - c7n9{r7 .} ==> r9c7≠3
biv-chain[4]: r4n8{c3 c2} - r4n4{c2 c9} - b9n4{r9c9 r9c7} - r9n9{c7 c3} ==> r9c3≠8
biv-chain[3]: b8n6{r8c4 r9c5} - r9c3{n6 n9} - r5n9{c3 c4} ==> r5c4≠6
hidden-single-in-a-column ==> r8c4=6
hidden-single-in-a-block ==> r7c4=8
naked-pairs-in-a-block: b8{r9c5 r9c6}{n1 n3} ==> r8c6≠3, r8c6≠1, r7c5≠1
stte
The simplest 1-step whip solution requires a whip[7]:
- Code: Select all
whip[7]: r9n9{c7 c3} - r5n9{c3 c4} - c4n6{r5 r8} - c4n8{r8 r7} - r7n1{c4 c5} - r9c6{n1 n3} - r9c5{n3 .} ==> r7c7≠9
stte
Absurd for a puzzle on the very easy side of W4
- denis_berthier
- 2010 Supporter
- Posts: 4665
- Joined: 19 June 2007
- Location: Paris
Re: Puzzle 21
Hi all,
Here is another way to solve the puzzle using the 9r5c4 which seems unavoidable.
(-9r5c4)->9r5c3->[ 9r9c7->4r9c9->4r4c2->8r4c3 ]->6r9c3->6r8c4... => -6r5c4 => r8c4=6, btte
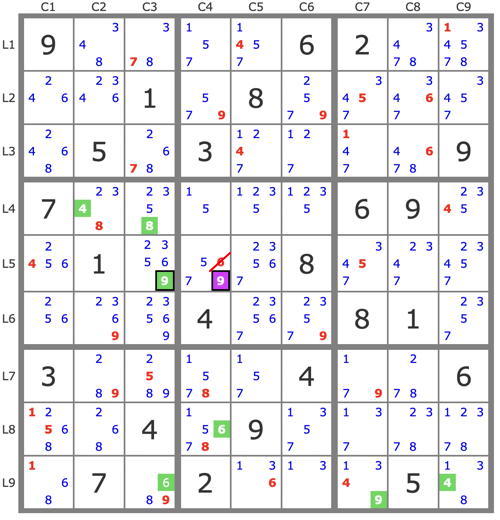
Robert
Here is another way to solve the puzzle using the 9r5c4 which seems unavoidable.
(-9r5c4)->9r5c3->[ 9r9c7->4r9c9->4r4c2->8r4c3 ]->6r9c3->6r8c4... => -6r5c4 => r8c4=6, btte

Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
5 posts
• Page 1 of 1

