The New Sudoku Players' Forum

[P.O.]

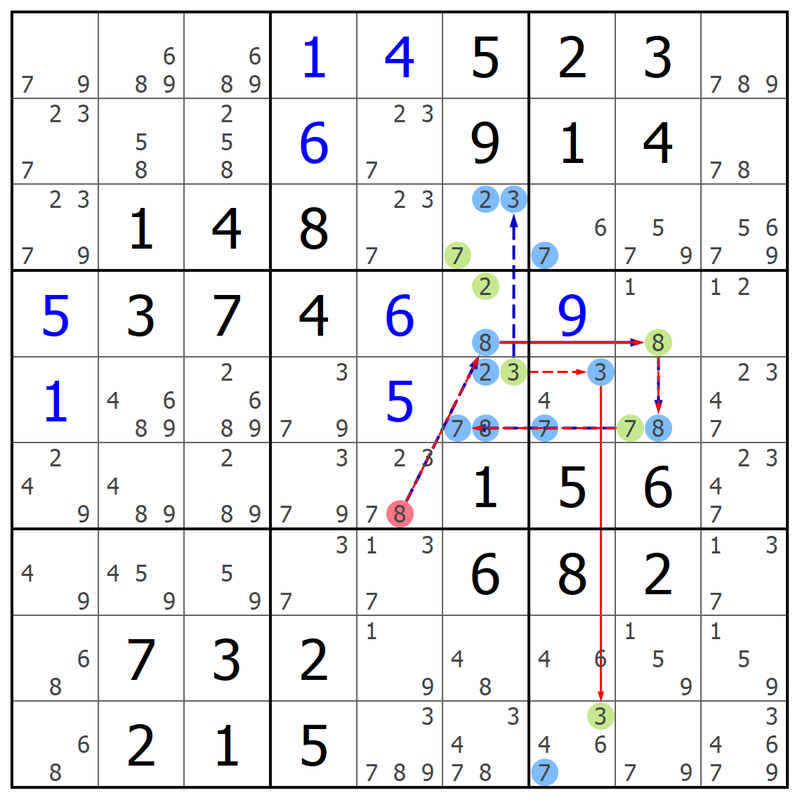
Code: Select all

.  .  .  .  .  5  2  3  .
.  .  .  .  .  9  1  4  .
.  1  4  8  .  .  .  .  .
.  3  7  4  .  .  .  .  .
.  .  .  .  .  .  .  .  .
.  .  .  .  .  1  5  6  .
.  .  .  .  .  6  8  2  .
.  7  3  2  .  .  .  .  .
.  2  1  5  .  .  .  .  .

.....523......914..148......374...................156......682..732......215.....


basics:

Hidden Text: Show

Code: Select all

( n9r4c7   n4r1c5   n1r1c4 )

intersections:
((((8 0) (4 8 6) (1 8)) ((8 0) (5 8 6) (1 7 8)))
 (((8 0) (8 1 7) (4 5 6 8 9)) ((8 0) (9 1 7) (4 6 8 9)))
 (((6 0) (8 1 7) (4 5 6 8 9)) ((6 0) (9 1 7) (4 6 8 9)))
 ( n1r5c1   n6r2c4   n5r4c1   n5r5c5   n6r4c5 )
 (((6 0) (3 7 3) (6 7)) ((6 0) (3 9 3) (5 6 7 9)))
 (((5 0) (8 8 9) (1 5 9)) ((5 0) (8 9 9) (1 4 5 6 9)))
 (((5 0) (3 8 3) (5 7 9)) ((5 0) (3 9 3) (5 6 7 9))))

TRIPLET ROW: ((7 1 7) (4 9)) ((7 2 7) (4 5 9)) ((7 3 7) (5 9))
(((7 4 8) (3 7 9)) ((7 5 8) (1 3 7 9)) ((7 9 9) (1 3 4 7 9)) ((8 1 7) (4 6 8 9)) ((9 1 7) (4 6 8 9)))

intersection:
((((9 0) (8 5 8) (1 8 9)) ((9 0) (9 5 8) (3 7 8 9))))

TRIPLET ROW: ((8 1 7) (6 8)) ((8 6 8) (4 8)) ((8 7 9) (4 6))
(((8 5 8) (1 8 9)) ((8 9 9) (1 4 5 6 9)))


Code: Select all

79     689    689    1      4      5      2      3      789             
237    58     258    6      237    9      1      4      78             
2379   1      4      8      237    237    67     579    5679           
5      3      7      4      6      28     9      18     12             
1      4689   2689   379    5      2378   347    78     2347           
249    489    289    379    2378   1      5      6      2347           
49     459    59     37     137    6      8      2      137             
68     7      3      2      19     48     46     159    159             
68     2      1      5      3789   3478   3467   79     34679       


[SteveG48]

Code: Select all

 *--------------------------------------------------------------------*
 |f79    g689^  g689^   | 1      4      5      | 2      3      789    |
 |f237@   58     258    | 6     e237@   9      | 1      4      78     |
 |f2379@  1      4      | 8     e237@  d237    | 67     579    5679   |
 *----------------------+----------------------+----------------------|
 | 5      3      7      | 4      6    ab28     | 9     b18     12     |
 | 1      4689^  2689^  | 379    5    cd2378   | 347   b78     2347   |
 | 249   h489   h289    | 379    237-8  1      | 5      6      2347   |
 *----------------------+----------------------+----------------------|
 | 49     459    59     | 37     137    6      | 8      2      137    |
 | 68     7      3      | 2      19     48     | 46     159    159    |
 | 68     2      1      | 5      3789   3478   | 3467   79     34679  |
 *--------------------------------------------------------------------*


Double UR using internals and externals. 23r23c15 and 86r15c23

[8r4c6 = 2r4c6&(87)r45c8 - (2|7=8*)r53c6] = *(3,7)r53c6 - 7r23c5 =[UR]= (79)r123c1 - 9r1c23 =[UR]= 8r6c23 => -8 r6c5 ; ste

[Cenoman]

Outstanding !
I like the double UR guardian chaining

[P.O.]

Code: Select all

8r6c5 => b2p589 <> 7
 r6c5=8 - r4n8{c6 c8} - r5c8{n8 n7} - 23r45c6 |- b2n3{r3c6 r23c5} - 179r789c5
                                              |- c7n3{r5 r9} - c7n7{r9 r3}
=> r6c5 <> 8
ste.


[SteveG48]

P.O. , while I can usually figure out your notation, I have to admit that I'm having trouble this time, though I do like the approach.

In any case, your solution inspired this:

8r45c6 = 2r4c6&8r6c5&(87)r45c8 - (2|7|8=3*4)r5c67 - (3|7)r5c7 = (37)r39c7 - (*3|7=28)r34c6 => -8 r6c5,r89c6 ; ste

[yzfwsf]

Braid[7]: => r6c5<>8;stte
8r6c5 - r4c6{n8=n2} - 8r4{r4c6=r4c8} - r5c8{n8=n7} - r5c6{n7=n3} - r3c6{n3=n7} - 3c7{r5c7=r9c7} - 7c7{r9c7=.}

[P.O.]

usually a contradictory candidate can be proved so in many ways, yzfwsf braid is very fine but the structure of a braid is more complex than that of an ordinary chain and i had found such an ordinary chain.

here my explanation of what i did:
the claim is that if r6c5=8 then b2 is emptied of 7s which proves that n8r6c5 is contradictory, its elimination solve the puzzle with singles
here the output of the solver, from r6c5=8 two chains eliminate the three 7s in b2, these two chains have four links in common

Code: Select all

((8 0) (6 5 5) (2 3 7 8))       r6c5=8
((8 1 1) (4 8 6) (1 8))         r4c8=8   because n8r4c6 is eliminated by r6c5=8
((7 2 9) (5 8 6) (7 8))         r5c8=7   because n8r5c8 is eliminated by r4c8=8
((3 3 82) (5 6 5) (2 3 7 8))    r5c6=3   because r6c5=8 and r5c8=7 eliminate n7 and n8 from r45c6 setting n2 in r4c6 and n3 in r5c6


then the last two links are different:

Code: Select all

((3 4 1) (9 7 9) (3 4 6 7))        r9c7=3   because n3r5c7 is eliminated by r5c6=3
((7 5 10) (3 7 3) (6 7))           r3c7=7   because n7r9c7 is eliminated by r9c7=3 and n7r5c7 is eliminated by r5c8=7

((3 4 2 2) ((2 5 2) (2 3 7)) ((3 5 2) (2 3 7)))       one of r23c5=3 because n3r3c6 is eliminated by r5c6=3
((7 5 2 62) ((7 5 8) (1 3 7)) ((9 5 8) (3 7 8 9)))    179r789c5 because r6c5=8 and r23c5=3 eliminate n8 and n3 from r789c5


i must admit that i too have some difficulty understanding your notation
can you decipher this riddle for me?

Code: Select all

8r45c6 = 2r4c6&8r6c5&(87)r45c8 - (2|7|8=3*4)r5c67 - (3|7)r5c7 = (37)r39c7 - (*3|7=28)r34c6 => -8 r6c5,r89c6


[SteveG48]

i must admit that i too have some difficulty understanding your notation
can you decipher this riddle for me?
[code]
8r45c6 = 2r4c6&8r6c5&(87)r45c8 - (2|7|8=3*4)r5c67 - (3|7)r5c7 = (37)r39c7 - (*3|7=28)r34c6 => -8 r6c5,r89c6

I hope so.

The first two terms establish 2, 7, and 8 at r4c6, r5c8, and r6c5 respectively. The next term, (2|7|8=3*4)r5c67, says that since r5c67 can't be 2 or 7 or 8, then they must be 3 and 4. The star indicates that we should remember the 3 when we look farther to the right. The next two terms, (3|7)r5c7 = (37)r39c7, may be the most confusing. Since r5c7 is a 4, it can't be either a 3 or a 7. That leaves us with a hidden pair 37 at r39c7. Finally, in the last term, (*3|7=28)r34c6, the star says look to the left where 3 has been established. Since r3c6 can't be either 7 or 3, it must be 2, and r4c6 is then 8. Therefore, either r4c6 or r5c6 must be 8.

[P.O.]

thank you, i will take the time to fully understand your fairly complex construction.