- Code: Select all
7 . . . . 4 . . 5
. 5 . 6 9 . . 1 .
. . 1 . . . 3 . .
. 2 4 . 3 . . 6 .
3 . . . . 1 . . 2
. . . . . . 8 . .
. . . 7 . . 2 . .
5 . 2 . . 6 . . 9
. 1 . . 8 . . 4 .
7....4..5.5.69..1...1...3...24.3..6.3....1..2......8.....7..2..5.2..6..9.1..8..4.
7 3689 3689 1238 12 4 69 289 5
248 5 38 6 9 2378 47 1 478
24689 4689 1 258 257 2578 3 2789 4678
189 2 4 589 3 5789 1579 6 17
3 6789 56789 4589 4567 1 4579 579 2
169 679 5679 2459 24567 2579 8 3579 1347
4689 34689 3689 7 145 359 2 358 1368
5 3478 2 134 14 6 17 378 9
69 1 3679 2359 8 2359 567 4 367
Puzzle 137
5 posts
• Page 1 of 1
Puzzle 137
- P.O.
- Posts: 2121
- Joined: 07 June 2021
Re: Puzzle 137
- Code: Select all
+--------------------------+------------------------+-----------------------+
| 7 3689 3689 | 1238 2-1 4 | e69 d289 5 |
| 248 5 38 | 6 9 2378 | 47 1 478 |
| 24689 4689 1 | 258 257 2578 | 3 d2789 4678 |
+--------------------------+------------------------+-----------------------+
| 189 2 4 | 589 3 5789 | 1579 6 c17* |
| 3 6789 56789 | 4589 4567 1 | 4579 c579* 2 |
| 169 679 5679 | 2459 24567 2579 | 8 c3579* 1347 |
+--------------------------+------------------------+-----------------------+
| 4689 34689 3689 | 7 ga145 359 | 2 f358 b1368 |
| 5 3478 2 | 34-1 g14 6 | c17* 378* 9 |
| 69 1 3679 | 2359 8 2359 | e567 4 367 |
+--------------------------+------------------------+-----------------------+
Almost W-Wing (*):
(1)r7c5 = r7c9 - [(1=7)r4c9 - r56c8 = r8c8 - (7=1)r8c7] = (72-9)r13c8 = (96-5)r19c7 = r7c8 - (5=41)r78c5 => -1 r1c5, r8c4; ste
Cenoman
- Cenoman
- Posts: 3210
- Joined: 21 November 2016
- Location: France
Re: Puzzle 137
- Code: Select all
*--------------------------------------------------------------------*
| 7 3689 3689 | 1238 2-1 4 | 69 289 5 |
| 248 5 38 | 6 9 2378 |d47 1 d478 |
| 24689 4689 1 | 258 257 2578 | 3 2789 d4678 |
*----------------------+----------------------+----------------------|
| 189 2 4 | 589 3 5789 | 1579 6 c17 |
| 3 6789 56789 | 4589 4567 1 | 4579 579 2 |
| 169 679 5679 | 2459 24567 2579 | 8 3579 1347 |
*----------------------+----------------------+----------------------|
| 4689 34689 3689 | 7 af145 359 | 2 e358 b1368 |
| 5 3478 2 | 34-1 f14 6 |c17 e378 9 |
| 69 1 3679 | 2359 8 2359 | 567 4 e367 |
*--------------------------------------------------------------------*
1r7c5 = r7c9 - (1=7*)r4c9&r8c7 - (7=486)b3c469 - (6|*7=385)b9p359 - (5=41)r78c5 => -1 r1c5,r8c4 ; ste
Steve
-

SteveG48 - 2019 Supporter
- Posts: 4620
- Joined: 08 November 2013
- Location: Orlando, Florida
Re: Puzzle 137
PO137 ER 8.4
It's unusual to see the simplest form of Sue de Coq at the outset of an ER 8.4 puzzle, but it provides an important elimination for what follows:
Sue de Coq:
(3689)r1c23, (69)r1c7, (38)r2c3 -> -8(r2c1,r3c12),-9(r1c8)
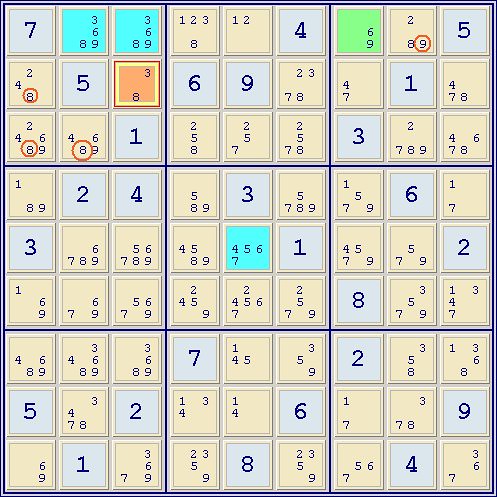
basic continuous AIC:
(1=2)r1c5-(2=8)r1c8-(8)r23c9=(8-1)r7c9=(1)r7c5 -> -2(r1c4),-8(r3c8),-36(r7c9),-1(r8c5)
EDIT => locked set for 6 in box 7 -> r9c1=9, r7c6=9
basic AIC:
(8)r4c1=ht(589)r4c467-(1)r4c7=(1)r8c7-(1=8)r7c9-(8)r8c7=(8)r8c2 -> -8(r7c1) stte
(Thanks to Steve: the locked set that I had mentioned wasn't necessary, actually is necessary for the final AIC. )
)
Nice puzzle P.O.!
- Code: Select all
*--------------------------------------------------------------------*
| 7 3689 3689 | 1238 12 4 | 69 289 5 |
| 248 5 38 | 6 9 2378 | 47 1 478 |
| 24689 4689 1 | 258 257 2578 | 3 2789 4678 |
|----------------------+----------------------+----------------------|
| 189 2 4 | 589 3 5789 | 1579 6 17 |
| 3 6789 56789 | 4589 4567 1 | 4579 579 2 |
| 169 679 5679 | 2459 24567 2579 | 8 3579 1347 |
|----------------------+----------------------+----------------------|
| 4689 34689 3689 | 7 145 359 | 2 358 1368 |
| 5 3478 2 | 134 14 6 | 17 378 9 |
| 69 1 3679 | 2359 8 2359 | 567 4 367 |
*--------------------------------------------------------------------*
It's unusual to see the simplest form of Sue de Coq at the outset of an ER 8.4 puzzle, but it provides an important elimination for what follows:
Sue de Coq:
(3689)r1c23, (69)r1c7, (38)r2c3 -> -8(r2c1,r3c12),-9(r1c8)

basic continuous AIC:
(1=2)r1c5-(2=8)r1c8-(8)r23c9=(8-1)r7c9=(1)r7c5 -> -2(r1c4),-8(r3c8),-36(r7c9),-1(r8c5)
EDIT => locked set for 6 in box 7 -> r9c1=9, r7c6=9
basic AIC:
(8)r4c1=ht(589)r4c467-(1)r4c7=(1)r8c7-(1=8)r7c9-(8)r8c7=(8)r8c2 -> -8(r7c1) stte
(Thanks to Steve: the locked set that I had mentioned wasn't necessary, actually is necessary for the final AIC.
Nice puzzle P.O.!
- DonM
- 2013 Supporter
- Posts: 487
- Joined: 13 January 2008
Re: Puzzle 137
thank you for your answers, my solution
sdc seems a nice technique, i'm not familiar with the many commonly used patterns, i find them hard to spot, but indeed this one once shown in this way is easily understandable and easy to memorize
- Code: Select all
r8c7{n1 n7} - r2c7{n7 n4} - b6n4{r5c7 r6c9} - r6n3{c9 c8} - 58r78c8 - 14r78c5 => r8c4 <> 1
ste.
sdc seems a nice technique, i'm not familiar with the many commonly used patterns, i find them hard to spot, but indeed this one once shown in this way is easily understandable and easy to memorize
- P.O.
- Posts: 2121
- Joined: 07 June 2021
5 posts
• Page 1 of 1

