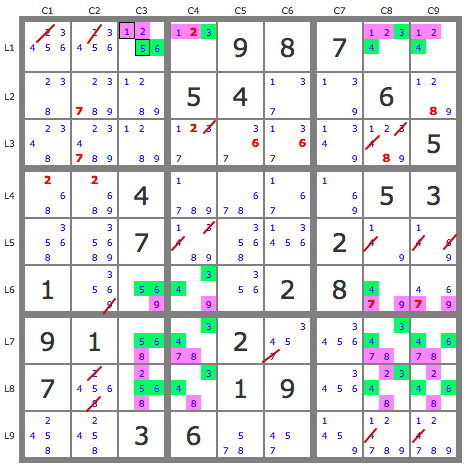
Hi Robert,
Mauriès Robert wrote:I find a msls on the subset r1678-c3489 for the partition 12789-3456 which eliminates the 16 candidates 2 r1c1, 2 r1c2, 9 r6c2, 7 r7c6, 2 r8c2, 8 r8c2, 3 r3c4, 3 r5c4, 4 r5c4, 3 r3c8, 4 r3c8, 4 r5c8, 4 r9c8, 4 r5c9, 6 r5c9, 4 r9c9 (see puzzle).
These are the same eliminations as those found by Leren, so what's the difference between this msls and this multifish, especially since Phil's solver finds the msls but not the multifish?
I'm really surprised that Phil's solver doesn't find the multifish. It's usually really good at that, and Phil's documentation of multifishes is the best I know. This is a very basic multifish, too, so I suspect some weird bug.
The difference between your MSLS and Leren's Multifish is in the sets of truths and links they use to form the 16x16 Rank 0 structure. Yours uses 16 cells as truths and Leren's uses 4 rows for 4 digits (4x4 = 16). The candidates in those sets are slightly different, so they need partly different linksets to cover them. Yours uses rows and columns to cover the candidates in the truth cells, while Leren's uses columns and cells to cover the truth rows.
Despite the different structures they produce the same eliminations, which is very common in these situations. If a Rank 0 pattern exists, it usually has many equivalent forms. Here's how I see the two forms in this case (* marks truths and \ marks links):
- Code: Select all
\56 \34 \34 \46
.------------------------.----------------------.--------------------------.
| 3456-2 3456-2 *1256 | *123 9 8 | 7 *1234 *124 | \12
| 238 23789 1289 | 5 4 137 | 139 6 1289 |
| 2348 234789 1289 | 127-3 367 1367 | 1349 1289-34 5 |
:------------------------+----------------------+--------------------------:
| 268 2689 4 | 1789 678 167 | 169 5 3 |
| 3568 35689 7 | 189-34 3568 13456 | 2 19-4 19-46 |
| 1 356-9 *569 | *349 356 2 | 8 *479 *4679 | \79
:------------------------+----------------------+--------------------------:
| 9 1 *568 | *3478 2 345-7 | 3456 *3478 *4678 | \78
| 7 456-28 *2568 | *348 1 9 | 3456 *2348 *2468 | \28
| 2458 2458 3 | 6 578 457 | 1459 12789-4 12789-4 |
'------------------------'----------------------'--------------------------'
MSLS: 16x16 {1678N3489 \ 12r1 79r6 78r7 28r8 56c3 34c48 46c9} => 16 elims
- Code: Select all
\1n \268n \56 \34 \6n \7n \78n \34 \46
.-------------------------.-----------------------.-------------------------.
| \3456-2 \3456-2 1256 | 123 9 8 | 7 1234 124 | *3456
| 238 23789 1289 | 5 4 137 | 139 6 1289 |
| 2348 234789 1289 | 127-3 367 1367 | 1349 1289-34 5 |
:-------------------------+-----------------------+-------------------------:
| 268 2689 4 | 1789 678 167 | 169 5 3 |
| 3568 35689 7 | 189-34 3568 13456 | 2 19-4 19-46 |
| 1 \356-9 569 | 349 \356 2 | 8 479 4679 | *3456
:-------------------------+-----------------------+-------------------------:
| 9 1 568 | 3478 2 \345-7 | \3456 3478 4678 | *3456
| 7 \456-28 2568 | 348 1 9 | \3456 2348 2468 | *3456
| 2458 2458 3 | 6 578 457 | 1459 12789-4 12789-4 |
'-------------------------'-----------------------'-------------------------'
MF(R): 16x16 {3456R1678 \ 56c3 34c48 46c9 1n1 268n2 6n5 7n6 78n7} => 16 elims
Personally I prefer multifishes, because they're easier and quicker to find and use manually, at least for me.
--
Edit. Fixed a typo in the MF: 1689 -> 1678.