Given:
...|..2|.96
76.|...|2..
.4.|..8|...
-----------
8.1|39.|..2
2..|...|..7
6..|.24|9.1
-----------
...|1..|.8.
..5|...|.74
37.|4..|...
Current position
...|742|.96
76.|...|248
.42|..8|71.
-----------
851|397|462
294|...|837
637|824|951
-----------
42.|17.|.8.
..5|2..|.74
37.|4..|12.
Can’t find any clue to go further. Please help.
(This is a "tough" one from the Telegraph)
Please help with this one
6 posts
• Page 1 of 1
Some Telegraph sudokus need trial and error to solve them. According to http://sudoku.sourceforge.net this is one of those times. Disappointing, isn't it?
- PaulIQ164
- Posts: 533
- Joined: 16 July 2005
Here's another attempt to show a logical method of finding forcing chains rather than just giving them. I found this solution with pencil and paper. From the given position I was able to remove only a couple more candidates by typical means before locking for a forcing chain:
1) Ignore all cells except those with exactly two candidates.
2) Connect cells within BINARY GROUPS -- pairs, trips, quads, etc. with BLUE LINES. I define a "binary group" as a set of cells that when considered together, can exist in exacty two states. For example, three cells in a row with the candidates [12][23][13] can only exist as 1-2-3 or 2-3-1.

The binary groups are:
Rows: r1c1237, r3c1459
Columns: r138c1, r18c2, r235c4
Boxes: (r1c234-r2c3-r3c1), (r1c7-r3c9)
(Note: Lines between r1c1-r1c7, r3c1-r3c9, etc are assumed but omitted for clarity.)
3) Exactly one of r1c1 and r1c2 must be a '1'.
Exactly one of r8c1 and r8c2 must be a '1'.
This forms an x-wing in 1's. Though it won't allow us to exclude any candidates, it does allow us to connect r8c1-r8c2 with a blue line, as the four cells taken together have exactly two states -- 1-8-9-1 or 5-1-1-8.
4) Similar logic allows a blue line to be drawn between r2c3-r2c4. No more blue lines can be drawn.

This is one large binary group. A chain can be in any fashion folloing the blue lines without forming a proof. The entire structure can exist in two states without internal contradiction.
5) RED lines are drawn between all other possible connections. r8c1-r7c3-r2c3, r1c7-r8c7 and r3c9-r9c9.
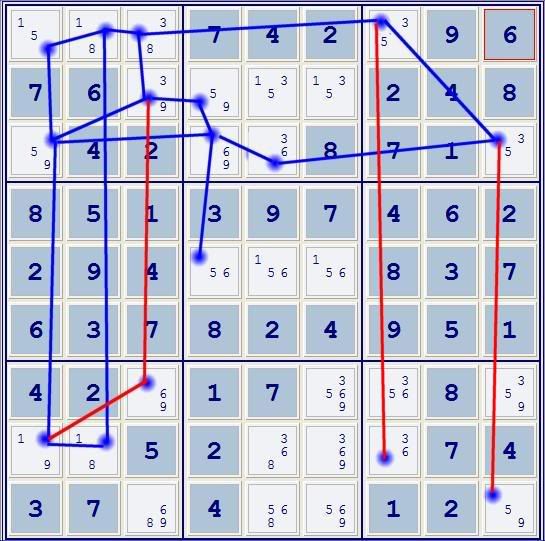
To form a proof, either from forcing chains or proof by contradiction, a LOOP must be formed. Two cells must be connected by two paths, at least ONE of which must contain RED lines. A loop that follows only blue lines is a binary group and can exist in two non-contradictory states.
6) Though a loop has been formed that includes a red line through r7c3, it cannot be used because the candidate 6 doesn't pair with any other.
At this point, we come to the end of the logic I can do using my standard method for finding forcing chains using 2-candidate cells. No chain exists. One might say that it didn't work. I would argue that it did! It proved that a 2-candidate forcing chain *does not exist*, and I can stop looking for it and try something else. The limitation in this method is that it does miss other types of forcing chains that use cells with more than 2 candidates.
I'm forced to consider the cells with 3 candidates. r8c5 seems promising as each of its candidates match-up with a 2-candidate cell in its row or column.
7) r3c5 and r1c7 must BOTH be 3 or NEITHER is 3. This is because they are part of a binary group and are connected directly by r3c9.
a) If they are BOTH 3, then r8c7=6, then r8c6<>6.
b) If NEITHER are 3, then r3c5=6, then r8c6<>6.
I now eliminate candidate 6 from r8c6 and add RED lines between it and r8c2, r3c5 and r8c7.
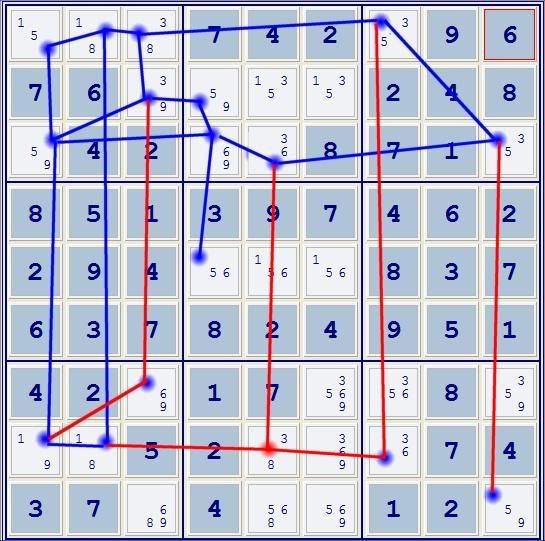
The RED path through r8c7 cannot be used as the candidate 6 doesn't pair with any other.
This leaves one red path between r8c2 and r3c5.
8)
r8c2=8 => r8c5=3 => r3c5=6
r8c2=1 => r1c2=8 => r1c3=3 => r1c7=5 => r3c9=3 => r3c5=6
Therefore, r3c5=6
The rest is easy.
1) Ignore all cells except those with exactly two candidates.
2) Connect cells within BINARY GROUPS -- pairs, trips, quads, etc. with BLUE LINES. I define a "binary group" as a set of cells that when considered together, can exist in exacty two states. For example, three cells in a row with the candidates [12][23][13] can only exist as 1-2-3 or 2-3-1.

The binary groups are:
Rows: r1c1237, r3c1459
Columns: r138c1, r18c2, r235c4
Boxes: (r1c234-r2c3-r3c1), (r1c7-r3c9)
(Note: Lines between r1c1-r1c7, r3c1-r3c9, etc are assumed but omitted for clarity.)
3) Exactly one of r1c1 and r1c2 must be a '1'.
Exactly one of r8c1 and r8c2 must be a '1'.
This forms an x-wing in 1's. Though it won't allow us to exclude any candidates, it does allow us to connect r8c1-r8c2 with a blue line, as the four cells taken together have exactly two states -- 1-8-9-1 or 5-1-1-8.
4) Similar logic allows a blue line to be drawn between r2c3-r2c4. No more blue lines can be drawn.

This is one large binary group. A chain can be in any fashion folloing the blue lines without forming a proof. The entire structure can exist in two states without internal contradiction.
5) RED lines are drawn between all other possible connections. r8c1-r7c3-r2c3, r1c7-r8c7 and r3c9-r9c9.

To form a proof, either from forcing chains or proof by contradiction, a LOOP must be formed. Two cells must be connected by two paths, at least ONE of which must contain RED lines. A loop that follows only blue lines is a binary group and can exist in two non-contradictory states.
6) Though a loop has been formed that includes a red line through r7c3, it cannot be used because the candidate 6 doesn't pair with any other.
At this point, we come to the end of the logic I can do using my standard method for finding forcing chains using 2-candidate cells. No chain exists. One might say that it didn't work. I would argue that it did! It proved that a 2-candidate forcing chain *does not exist*, and I can stop looking for it and try something else. The limitation in this method is that it does miss other types of forcing chains that use cells with more than 2 candidates.
I'm forced to consider the cells with 3 candidates. r8c5 seems promising as each of its candidates match-up with a 2-candidate cell in its row or column.
7) r3c5 and r1c7 must BOTH be 3 or NEITHER is 3. This is because they are part of a binary group and are connected directly by r3c9.
a) If they are BOTH 3, then r8c7=6, then r8c6<>6.
b) If NEITHER are 3, then r3c5=6, then r8c6<>6.
I now eliminate candidate 6 from r8c6 and add RED lines between it and r8c2, r3c5 and r8c7.

The RED path through r8c7 cannot be used as the candidate 6 doesn't pair with any other.
This leaves one red path between r8c2 and r3c5.
8)
r8c2=8 => r8c5=3 => r3c5=6
r8c2=1 => r1c2=8 => r1c3=3 => r1c7=5 => r3c9=3 => r3c5=6
Therefore, r3c5=6
The rest is easy.
- tso
- Posts: 798
- Joined: 22 June 2005
6 posts
• Page 1 of 1

