The New Sudoku Players' Forum

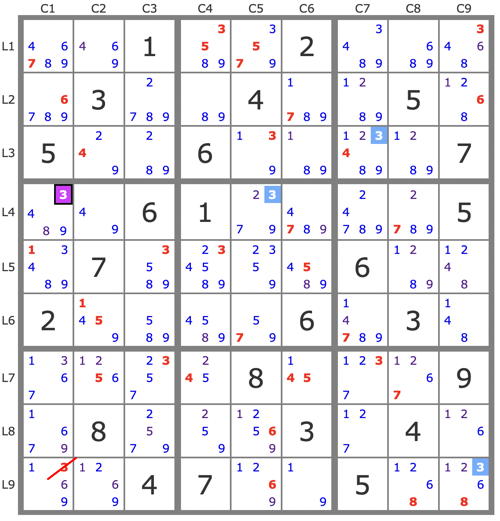
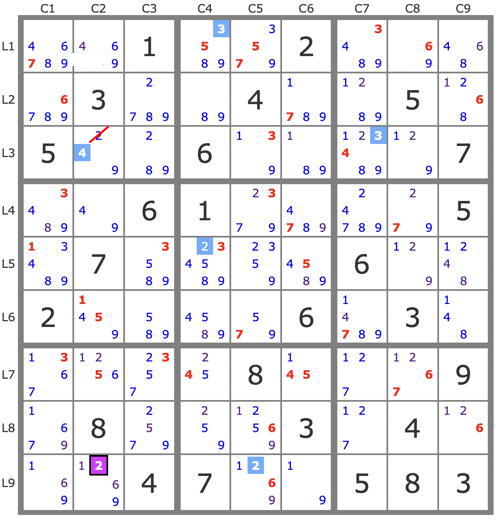
[m_b_metcalf]

Code: Select all

 . . 1 . . 2 . . .
 . 3 . . 4 . . 5 .
 5 . . 6 . . . . 7
 . . 6 1 . . . . 5
 . 7 . . . . 6 . .
 2 . . . . 6 . 3 .
 . . . . 8 . . . 9
 . 8 . . . 3 . 4 .
 . . 4 7 . . 5 . .

..1..2....3..4..5.5..6....7..61....5.7....6..2....6.3.....8...9.8...3.4...47..5..

A curiosity from the current Patterns Game. Not a one-step pony, and not for the faint-hearted.

Mike

[Mauriès Robert]

Hi Mike,
Here is my two-step solution with TDP:

(-3r4c1)->3r4c5->3r3c7->3r9c9->... => -3r9c1 => r9c9=3, r9c8=8

puzzle1: Show

(-2r9c2)->2r9c5->2r5c4->3r1c4->3r3c7->4r3c2->... => -2r3c2 => r1c2=6, stte

puzzle2: Show

Robert

[P.O.]

Code: Select all

my solution is 2 forcing chains + basics:

46789   469     1      a+3589   3579    2       3489    689    b-3468             
6789    3       2789    89      4       1789    1289    5       1268             
5       249     289     6       139     189     123489  1289    7               
3489    49      6       1       2379    4789    24789   2789    5               
13489   7      B-3589  A2+34589 2359    4589    6       1289    1248             
2       1459    589     4589    579     6       14789   3       148             
1367    1256   B2+357   245     8       145     12×37   1267    9               
1679    8       2579    259     12569   3       127     4       126             
1×369   1269    4       7       1269    19      5       1268   b12+368           

r15c4n3 => r7c7 r9c1 <> 3
 r1c4=3 - c9n3{r1 r9}
 r5c4=3 - c3n3{r5 r7}

singles: ( n3r9c9  n8r9c8 )

46789   469     1      a+3589    3579    2       3489    69      468             
6789    3       2789    89       4       1789    1289    5       1268             
5      c×2+49   289     6       b1-39    189    b12+3489 129     7               
3489    49      6       1       B*2379   4789    24789   279     5               
13489   7       3589   A2+34589 B*2359   4589    6       129     1248             
2       1459    589     4589     579     6       14789   3       148             
1367    1256    2357    245      8       145     127     1267    9               
1679    8       2579    259      12569   3       127     4       126             
169    C1+269   4       7       C1-269   19      5       8       3               

r15c4n3 => r3c2 <> 2
 r1c4=3 - r3n3{c5 c7} - r3n4{c7 c2}
 r5c4=3 - b5n2{r5c4 r45c5} - r9n2{c5 c2}

bte.


[denis_berthier]

A curiosity from the current Patterns Game. Not a one-step pony, and not for the faint-hearted.

SER = 7.5

Code: Select all

Resolution state after Singles and whips[1]:
   +----------------------+----------------------+----------------------+
   ! 46789  469    1      ! 3589   3579   2      ! 3489   689    3468   !
   ! 6789   3      2789   ! 89     4      1789   ! 1289   5      1268   !
   ! 5      249    289    ! 6      139    189    ! 123489 1289   7      !
   +----------------------+----------------------+----------------------+
   ! 3489   49     6      ! 1      2379   4789   ! 24789  2789   5      !
   ! 13489  7      3589   ! 234589 2359   4589   ! 6      1289   1248   !
   ! 2      1459   589    ! 4589   579    6      ! 14789  3      148    !
   +----------------------+----------------------+----------------------+
   ! 1367   1256   2357   ! 245    8      145    ! 1237   1267   9      !
   ! 1679   8      2579   ! 259    12569  3      ! 127    4      126    !
   ! 1369   1269   4      ! 7      1269   19     ! 5      1268   12368  !
   +----------------------+----------------------+----------------------+
218 candidates.

1) Simplest-first solution in S+Z4 (using only reversible patterns):

Code: Select all

finned-x-wing-in-columns: n5{c6 c2}{r7 r5} ==> r5c3≠5
whip[1]: r5n5{c6 .} ==> r6c4≠5, r6c5≠5
finned-swordfish-in-columns: n3{c3 c4 c7}{r7 r5 r1} ==> r1c9≠3
singles ==> r9c9=3, r9c8=8
finned-x-wing-in-columns: n6{c8 c2}{r1 r7} ==> r7c1≠6
finned-swordfish-in-rows: n7{r6 r1 r8}{c7 c5 c1} ==> r7c1≠7
z-chain[3]: r9c6{n9 n1} - r3c6{n1 n8} - r2c4{n8 .} ==> r2c6≠9
biv-chain[4]: r4c2{n9 n4} - r3n4{c2 c7} - r3n3{c7 c5} - r4n3{c5 c1} ==> r4c1≠9
biv-chain[4]: r1n7{c1 c5} - r6n7{c5 c7} - c8n7{r4 r7} - c8n6{r7 r1} ==> r1c1≠6
biv-chain[4]: b1n6{r2c1 r1c2} - c8n6{r1 r7} - c8n7{r7 r4} - c6n7{r4 r2} ==> r2c1≠7
z-chain[4]: c7n3{r1 r3} - b3n4{r3c7 r1c9} - r1c2{n4 n6} - r1c8{n6 .} ==> r1c7≠9
z-chain[4]: r9n6{c2 c5} - r9n2{c5 c2} - c2n1{r9 r6} - c2n5{r6 .} ==> r7c2≠6
w1-tte

I could indeed find no 1-step solution (there's no W1 anti-backdoor).

2) 2-step solutions
There are 6 2-step (more precisely 2-elimination) solutions in S+W6:
- 4 starting with a swordfish in columns:

Code: Select all

finned-swordfish-in-columns: n3{c3 c4 c7}{r7 r5 r1} ==> r1c9≠3
singles ==> r9c9=3, r9c8=8
whip[6]: b1n6{r1c1 r2c1} - r7n6{c1 c2} - r9n6{c2 c5} - r9n2{c5 c2} - c2n1{r9 r6} - c2n5{r6 .} ==> r1c8≠6
OR:
whip[6]: r2n6{c9 c1} - r7n6{c1 c2} - r9n6{c2 c5} - r9n2{c5 c2} - c2n1{r9 r6} - c2n5{r6 .} ==> r8c9≠6
w1-tte

Code: Select all

finned-swordfish-in-columns: n3{c4 c9 c3}{r5 r1 r9} ==> r9c1≠3
singles ==> r9c9=3, r9c8=8
whip[6]: r2n6{c9 c1} - r7n6{c1 c2} - r9n6{c2 c5} - r9n2{c5 c2} - c2n1{r9 r6} - c2n5{r6 .} ==> r8c9≠6
OR:
whip[6]: r2n6{c9 c1} - r7n6{c1 c2} - r9n6{c2 c5} - r9n2{c5 c2} - c2n1{r9 r6} - c2n5{r6 .} ==> r1c8≠6
w1-tte

- and 2 starting with a swordfish in rows:

Code: Select all

finned-swordfish-in-rows: n3{r4 r3 r9}{c1 c5 c7} ==> r7c7≠3
singles ==> r9c9=3, r9c8=8
whip[6]: r2n6{c9 c1} - r7n6{c1 c2} - r9n6{c2 c5} - r9n2{c5 c2} - c2n1{r9 r6} - c2n5{r6 .} ==> r1c8≠6
OR
whip[6]: r2n6{c9 c1} - r7n6{c1 c2} - r9n6{c2 c5} - r9n2{c5 c2} - c2n1{r9 r6} - c2n5{r6 .} ==> r8c9≠6
w1-tte

Note that, in the last two groups of 2 solutions, only the target of the final whip is different.

[pjb]

1. Finned swordfish of 3s (r347\c157), fin at r7c3, => -3 r9c1
2. Discontinuous loop: (2)r9c2 = (2)r9c5 - (2)r78c4 = (2-3)r5c4 = (3)r1c4 - (3)r1c7 = (3-4)r3c7 = (4-2)r3c2 => -2 r3c2; btte

Phil

[Mauriès Robert]

Hi Phil,
So we have the same resolutions but expressed differently.
Cordialy
Robert