On question that has been asked many times goes something like this: "How do I know which cell to start to look for forcing chains?" or something like that. Here's one tactic that works very well in a narrow selection of situations.
If all the unsolved cells left are bivalue except one, you can use BUG. If two or more are still poly-value, BUG may or may not help. Either way, when there are only a handful of polyvalue cells and lots of bivalue cells, simple xy-type forcing chains will probably be easy to find in abundance.
Here's the paper-and-pencil method I still use to find xy-type forcing chains in just this situation -- lots of bivalue cells and small number of poly-value cells. I've refered to it before as BINARY GROUPS. It will only find xy-type forcing chains -- and it won't find all of them -- only the ones that use only the bivalue cells -- but in these situations, it will usually do the job.
- Code: Select all
+-------+-------+-------+
| . 3 9 | . 6 . | 4 . . |
| . 8 . | 2 9 4 | 3 . 7 |
| 4 . 7 | 8 1 3 | 5 9 . |
+-------+-------+-------+
| 8 . . | 3 2 6 | 9 7 1 |
| . . 3 | . 7 . | . . 4 |
| 6 7 1 | 9 4 8 | 2 5 3 |
+-------+-------+-------+
| 3 . . | . 8 . | 1 2 5 |
| . . 8 | . 5 2 | . 3 . |
| . . 2 | . 3 . | . 4 . |
+-------+-------+-------+
+----------------+----------------+----------------+
| 12 3 9 | 57 6 57 | 4 18 28 |
| 15 8 56 | 2 9 4 | 3 16 7 |
| 4 26 7 | 8 1 3 | 5 9 26 |
+----------------+----------------+----------------+
| 8 45 45 | 3 2 6 | 9 7 1 |
| 29 29 3 | 15 7 15 | 68 68 4 |
| 6 7 1 | 9 4 8 | 2 5 3 |
+----------------+----------------+----------------+
| 3 469 46 | 467 8 79 | 1 2 5 |
| 79 14 8 | 14 5 2 | 67 3 69 |
| 579 1569 2 | 16 3 19 | 78 4 89 |
+----------------+----------------+----------------+
There are four polyvalue cells left:
r7c2, r7c4, r9c1 and r9c2.
These four cells are in:
Rows 7 and 9
Columns 1, 2 and 4
Box 7 and 8
For the forcing chain to work, at least ONE of the links MUST take place within one of these 7 groups.
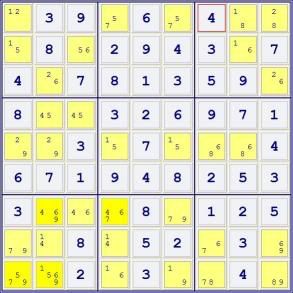
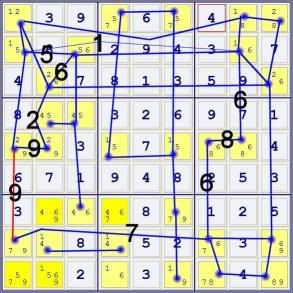
Step ONE -- connect all BIVALUE cells that form naked sets -- pairs, trips, quads, etc, in all rows, columns and boxes using BLUE LINES. The connections are drawn simplified. For example, 5 cells in a row forming a naked quint are connected by a single straight line rather than drawing each of the 10 intra-cell connections. (Two separate naked sets are NOT connected -- for instance, in the case of [12][12][34][45][35], the first two cells are not connected to the next three.)
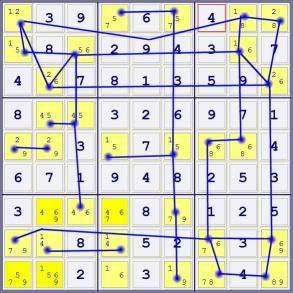
All the cells that are part of a single blue network can exist in exactly two states. This network is a BINARY GROUP.
Step TWO -- make any additional BLUE connections you can justify. In this case, connect r1c4 and r5c4. The four cells r15c46 contain an x-wing in 5s and can exist in exactly two states.
Examine the pair at r5c12 and the two cells r1c1, r2c3. Exactly one of the first pair must be 2 -- exactly one of the second pair must be 2. The four cells can exist in exactly two states, so they are connected by blue lines.
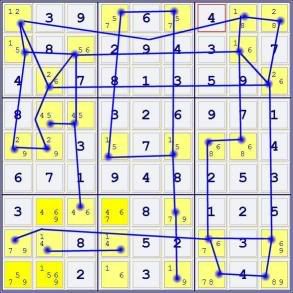
There are now three binary groups identified.
Step THREE -- make remaining connections between bivalue cells in RED.
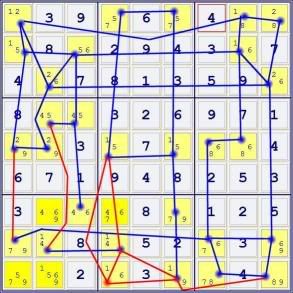
Step FOUR -- look for a closed loop that has at least one RED segment, preferably just one. In this case, the RED line connecting r58c1 is the only one that closes a loop by itself. The length of the loop does not matter. Unlike other methods of finding forcing chains, finding longer loops is no more difficult than finding shorter ones -- and might be subjectively more fun to identify.
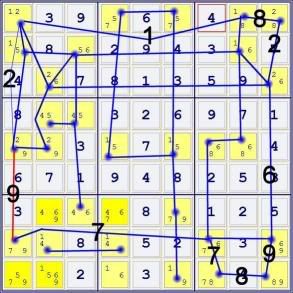
Step FIVE -- label the lines connecting the cells in the loop with the shared candidate. Here are two of many possibilities:
(Note that additial blue lines are drawn for clarity. These *could* have been drawn in advance, but are not to avoid the spaghetti-syndrome.)
When faced with a choice if labels or branches, make your picks so that consecutive lables repeat EXACTLY ONCE in the loop.
The cell between the identical lables contain the exclusion. In the first case, the labels are 9926516867 -- eliminating the '9' from r5c1. In the second case, the labels are 9218269877, eliminating the '7' from r8c7. After either one, the rest of the puzzle is singles.

