The New Sudoku Players' Forum

[gurth]

Notes on CW (Conjugate Worlds), latest version.

I first introduced this technique on the Eureka Forum in September 2006, under the name CCW (Comparison of Conjugate Worlds). After that, Bill Richter started calling it CW - a practice I have been aping myself lately.
That forum is now defunct and my work on it lost. And there seems to be no description of CCW extant anywhere today.
As I am now using this technique regularly on this forum, I decided to remedy the lack of definitive literature in this post.

How CW works:

I've used the puzzle "February 25, 2015", in the Puzzles Section, as an example to illustrate the use of CW.

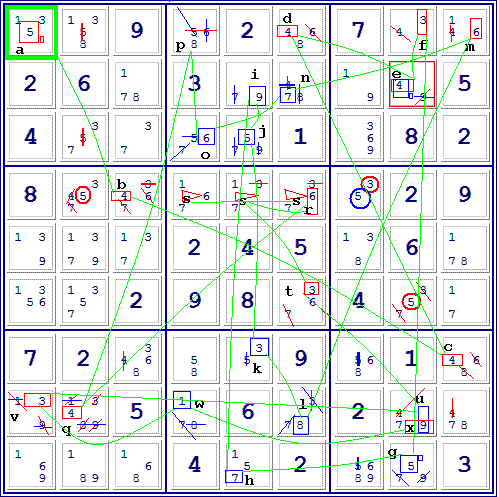
First, a conjugate pair is chosen, e.g. 111 and 711, using thick red and blue circles to show they are conjugate at start. All digits conjugate to these are added to the conjugate net, arriving at a blue set of equivalent digits (all true or all false) and a red set. "RR111" refers to a member of the red set.

Next, (see diagram), B442 means 442 is true if Blue is true; this single letter B also refers to the following digits, in this case -4r8c23 and 489. Observe how these facts are denoted in the picture: by '4 and 4 in blue.
d499 means delete 499.
BB413 means 413 has now become conjugate Blue: thin circles are used to show conjugates added to the original net.
eRR means Red is established as True. (here one might instead write e111, meaning that 111 is true)

BB413,B442,-4r8c23,489*.
d499(RR999),BB399,RR391,BB382,B-682,689*, eRR,stte.

[ArkieTech]

What software do you use to draw circles and lines?

[gurth]

What software do you use to draw circles and lines?

- Just "Paint", which seems to go with most Windows operating systems. I have an old (nearly 7 years) laptop with Windows Vista (Home Edition).

[ArkieTech]

What software do you use to draw circles and lines?

- Just "Paint", which seems to go with most Windows operating systems. I have an old (nearly 7 years) laptop with Windows Vista (Home Edition).

Thanks.

[gurth]

I am placing my CW solution of the puzzle 'February 28, 2015' (see Puzzles Section) on this thread as it illustrates my first use of Forward Clockwise Motion as a graphical display method:

CW:
RR368,R166,195,d145,RR645,R475,772*.
BB778,B472*:RR772,BB472,RR442,BB742,RR475,BB675,d665,776.
BB742,B949,-969,964,d664,e663,d683.
RR772,RR387,R-783,-383,dRR,eBB,eB; NStte.

Clockwise Motion is forward, Anti-Clockwise Motion is backward.
That is what the curves are for: my innovation for today. It's an aesthetic and easily visible way of recording the direction of each link, which enables you to trace the history of the whole system of chain and net links. From any point on any chain in the net, you can follow an anticlockwise motion which will bring you to the start of that chain.

[gurth]

Latest Advances in CW:
The markings indicating conditional cutting (deleting) and placing have now been revised to give more detail.

Cutting:
In general, any digit can be cut for 4 reasons:
1. This digit has already been placed in the same row,
2. """""""""""""""""""""""""""""""""""""""""""""""""""""""column,
3. """""""""""""""""""""""""""""""""""""""""""""""""""""""cell,
4. """""""""""""""""""""""""""""""""""""""""""""""""""""""box.
Case 1 is shown by a horizontal slash through the digit,
Case 2 """"""""""""""vertical"""""""""""""""""""""""""",
Case 3 """"""""""""""diagonal"""""""""""""""""""""""""",
Case 4 """"""""""""""longer diagonal""""""""""""""""""",
extending to the edge of the cell.

Placing:
In general, any digit can be placed for 4 reasons:
1. It is the last left in the row,
2. """""""""""""""""""""""""""column,
3. """""""""""""""""""""""""""cell,
4. """""""""""""""""""""""""""box.
Case 1 is shown by a horizontal rectangle,
Case 2 """"""""""""""""vertical"""""""""""",
Case 3 """"""""""""""""square,
Case 4 is shown by a square with a little square attached.

These new markings enable one to see the reasons for cutting and placing every digit at a glance.
The result is that there is no need for any explanatory text write-up), as every action can be clearly seen and understood from the diagram.

In my next post I'll explain how this is done with the aid of an example, in which CW will be applied to a puzzle rated SER 9.0 until one colour is contradicted. This will eliminate enough candidates to reduce the rating to 7.3. A second application of CW may or may not be enough to complete the solution of the puzzle: we'll see.

[gurth]

Example: 52s90cb: examine the picture:


1. The rule is to follow a single, unbranching chain starting at the candidate labelled A, through all the candidates
labelled with capital letters B,C etc up to the last capital (here E) and then to continue via labels a, b, c etc to the end, (here v). We may proceed only to placeable candidates, whether Red or Blue conditionals, or unconditional True (marked with Black). As we reach each new label, we must also mark all those candidates it deletes, whether conditionally or unconditionally, in the appropriate colour.

2. Starting at the A: this labels the conjugate Red254: the marking of the set of conjugates, with their deletions, is done prior to the derivations discussed here.

3. From A, follow the green line to candidate B, the Red272. It's in a red rectangle - horizontal, meaning it's the last red 2 in the row. Check r7 to verify this: the only other 2 in the row is slashed vertically, so we look from it vertically to see what has caused the slash. We see the candidate A. This assures us that the conditions for B were already in existence before we got to B, as A precedes B.

4. Follow from B to C. There is no candidate placed at C: strictly, we should have omitted C and continued our labelling at r9c6. So let's look at D. D labels 296 with a red circle, meaning a red conjugate. By this time,292 has been cut (slashed) by both red and blue cuts, which is an unconditional deletion, so that D is truly a red conjugate.

5. Follow to E, where 2 is labelled as blue conjugate. The green line ends here, and recommences at (a).

6. (a) states that 927 is a blue conditional, the square shows that it is the last candidate in the cell - the 1 has already been cut in r2 (due to the conjugate at r2c1).

7. (b) and (c) are straightforward. The green rectangle at (d) is an error, please just ignore it. We see the blue 8 in a horizontal rectangle, meaning it's the only blue 8 left in the row - and yes, we see that 859 was cut by the original blue conjugate 259.

8. And that's all there is to it - you can visit any cell, that contains a labelled candidate, and see immediately why that candidate has been placed.

9. It is not essential to mark all cuts caused by a placement - you can leave out those you will not need to rely on in future placements. So, for instance, I have not cut the 1 or 7 in r5c9.

10. The example ends at (v) as two blue 8s have appeared in box 8, confirming all reds as true, which leaves us with a puzzle rated SER 7.3. That will require another diagram.

[gurth]

Comments:
It was necessary to place 428,814,988,381 and delete 189r8c2, to reach this position at (x) (move 24) where only singles remain.
No contradictions were found, and I can't say (as I haven't checked to see) whether red or blue was true. It's not obvious from the diagram, as no colour has been confirmed or denied.

Note further innovations to CW:
Locked sets are now used, see "sss" at r4c456 using red triangles to show a red locked trip (167).

For more examples, watch the Puzzles Section for recent and future posts.