The New Sudoku Players' Forum

[speter]

G'Day Folks,

I am having trouble with Nice Loops...

The following image is Figure 1 on the Sudoku Wiki X-Cycles (part 2) page


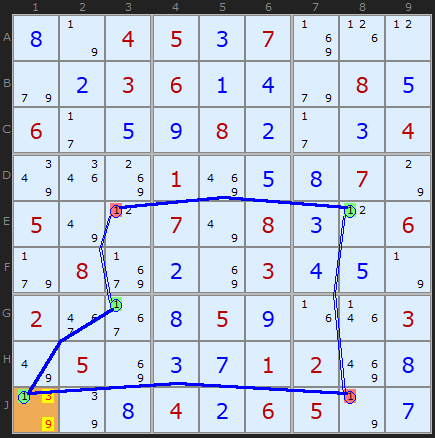
The page has the following rule (2):
"If the adjacent links are links with strong inference (solid line), a candidate can be fixed in the cell at the discontinuity."
In the example above this refers to r9c1.

When I study the 1's in this puzzle I get the following:

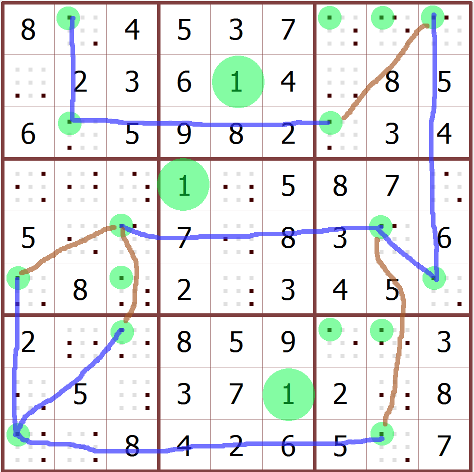
Green circles = instantiated or candidate 1's
Blue lines = strong links
Brown lines = weak links
(I am only showing defining weak links existing between strong links. I think for example there is a weak link between r5c3 & r6c3...)

I am wondering how/why the author chose to 'link' from r9c1 to r7c3 and not r6c1?
I don't think it would have altered the example.

In terms of the rule (listed above); r3c2, r9c1 and r6c9 all seem correctly match the rule; setting any of them to 1 "solves" the puzzle.
But, r5c8 also seems to match the rule, though it has 2 strong and 1 weak link.
I am thinking that the presence of the weak link means r5c8 can be considered a 'normal' node in the loop.

I am also wondering how one 'builds' the loop.
- r5c8 has 3 links - 1 weak and 2 strong
- r5c3 has 3 links - 2 weak and 1 strong
- r9c1 has 3 strong links
is it simply a matter of trying to alternate strong & weak links?

Steve

[JasonLion]

There are often enough many different ways to construct loops. In the end you simply pick one that is useful and ignore the others (for this one step) even if they are valid choices.

Because the upper branch isn't part of a loop you can't use it for this technique, leaving two valid ways to construct a loop in this specific example.

[Leren]

You raise a number of issues in your post, which it is too difficult to answer all at once in one post, so I'll just concentrate on a few points, which may help you a little bit.

"If the adjacent links are links with strong inference (solid line), a candidate can be fixed in the cell at the discontinuity."

This "rule" is just a fancy way of saying that if you start off by assuming that a candidate is False, and you subsequently deduce that it is True, then it must ultimately be True in the solution, so you can solve that cell with the candidate.

One confusing aspect of Andrew's diagram is that the 1 in r9c1 is just green. Strictly speaking, it starts out being red (False) being at the start of the Strong link to the 1 in r7c3 and turns Green (True) being at the end of the Strong link from the 1 in r9c8. Maybe he should have colored it yellow (red and green make yellow don't they ? ) and used some other color for the other candidates in r9c1.

Your point about alternating Strong and Weak links is correct. A loop is a special case of a more general construction called an Alternating Inference chain (AIC for short), which is exactly what you say, alternate Strong and Weak links.

I think I'll stop there, that's enough to chew on for one post.

leren