This one is great for binary groups and/or edge labeling. I think Mempham is intentionally making them at about this level for toughs and or diabololicals.
Using nothing beyond a naked pair, I got to this point:
- Code: Select all
7 5 3 | 4 8 . | 9 . 1
2 1 . | . 9 . | 4 . 3
4 . 9 | . 1 3 | 5 . 7
-------+-------+------
9 3 4 | . 2 . | 7 1 5
8 7 1 | 9 5 4 | 2 3 6
5 . . | . 3 . | 8 9 4
-------+-------+------
1 9 . | 3 7 . | 6 4 2
6 . 7 | . 4 . | 3 5 9
3 4 . | . 6 9 | 1 7 8
{7} {5} {3} {4} {8} {26} {9} {26} {1}
{2} {1} {68} {57} {9} {57} {4} {68} {3}
{4} {68} {9} {26} {1} {3} {5} {268} {7}
{9} {3} {4} {68} {2} {68} {7} {1} {5}
{8} {7} {1} {9} {5} {4} {2} {3} {6}
{5} {26} {26} {17} {3} {17} {8} {9} {4}
{1} {9} {58} {3} {7} {58} {6} {4} {2}
{6} {28} {7} {128} {4} {128} {3} {5} {9}
{3} {4} {25} {25} {6} {9} {1} {7} {8}
(There is an xy-wing at r38c24 that would exclude the candidate 2 from r8c4, but I didn't see it at the time. It isn't required to solve the puzzle.)
This method considers ONLY the cells with exactly 2-candidates, ignoring everything else.
Ok, first thing, make all connections in simple BINARY GROUPS in BLUE. A simple binary group is several cells in a row, column or box that can exist in only two states, for example: [12][23][34][14]
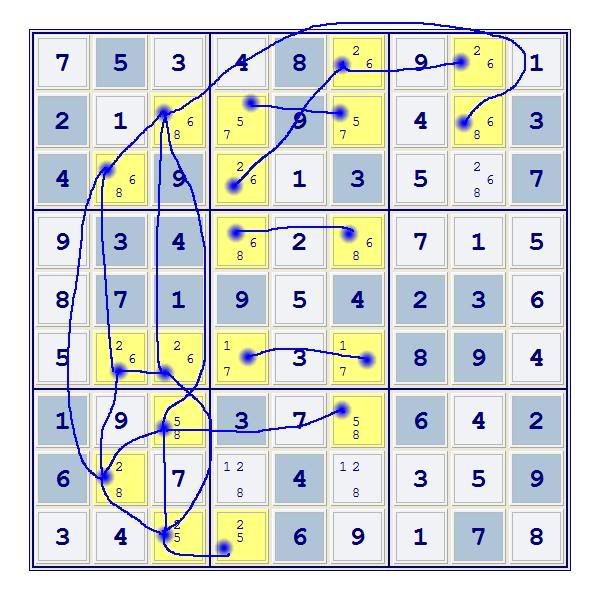
Now, make any additional BLUE connections that are part of the binary group:
-- the four cells of r26c46 each contain a candidate 7 and therefore can exist in only two states (7571 or 5717), so connect them with BLUE LINES.
-- the four cells of r1c6, r3c4 and r4c46 each contain a candidate 6 and therefore can exist in only two states, so connect them with BLUE LINES.
-- the four cells of r2c46, r7c6 and r9c4 each contain a candidate 5 and therefore can exist in only two states, so connect them with BLUE LINES.
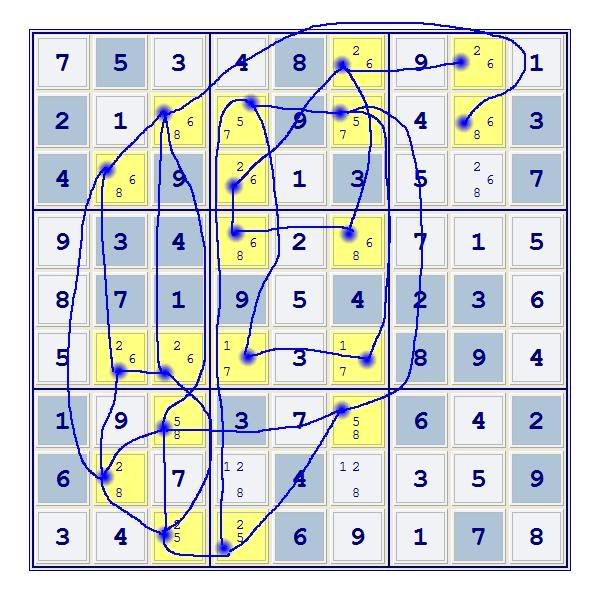
Make all remaining connections in RED. The loop we're looking for MUST contain at least on RED line.
The shortest loop containing the red line r12c8 is:
r1c8-r1c6-r3c4-r3c2-r2c3-r2c8
Each of these cells contains a candidate 6, so it can exist in exactly two states. Both red lines can be converted to blue lines.
I've edge labled the shortest loop using the red line r49c4:
Since the loop is non-repeating, that is, no two consecutive edges are the same, the red line can be changed to blue.
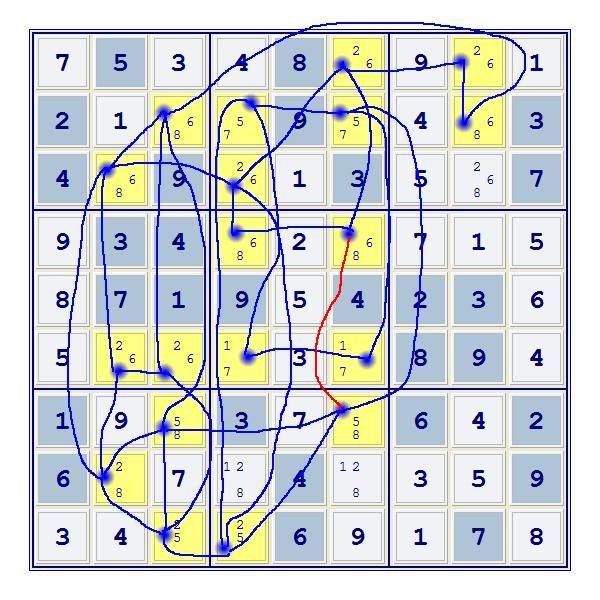
Only one red line left!
The shortest loop, which I've edge labeled, is:
As this loop repeats, either 88625 or 86625, forcing chains can be formed removing either the 6 from r4c4 or the 8 from r4c6, for example:
r7c6=5 => r9c4=2 => r3c4=6 => r4c4=8 => r4c6=6
r7c6=8 => r4c6=6
Therefore, r4c6=6.
All the rest is elementary.
by SoCalSudokuFan » Sat Aug 27, 2005 8:53 am 
or tell me conclusively that it's unsolvable without using Nishio (I suspect the latter is the case
).
