The New Sudoku Players' Forum

[McNessa]

I visited Angus Johnson's Simple Sudoko web site:

http://angusj.com/sudoku/hints.php

and found some very helpful solution techniques, but I am confused by his Naked Triple example.

In his example he states that if there only 3 squares within the illustrated group that contain the numbers 1, 4 & 6, therefore the 1 and the 4 can be removed from the remaining squares in the group.

The illustrated group also has 3 squares that only contain the numbers 1,5 & 7. How do I know which set of numbers is the true Naked Triple? If I follow the same logic using the numbers 1,5 & 7, I'd remove the number 1 from the squares the example indicates I should keep.

[PaulIQ164]

Assuming you're referring to this group:



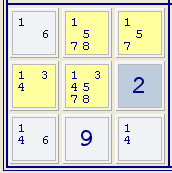
(sorry for leeching your bandwidth) then what I assume you're seeing doesn't count. Yes there are only three cells that have the 1 and the 5 and the 7 in them, but some of them can be other numbers as well. Notice that with the 1-4-6 triple, none of the cells can be anything other than 1 or 4 or 6.

[jimbobbadger]

In his example he states that if there only 3 squares within the illustrated group that contain the numbers 1, 4 & 6, therefore the 1 and the 4 can be removed from the remaining squares in the group.

What he's trying to get across is that all values in the hidden triple can be excluded from the rest of the 3x3. So 1, 4 and 6 can be eliminated from all other squares, it just happens in this example that 6 doesn't feature outside of the hidden triple.

[tso]

Here are four examples of a NAKED TRIPLE.

Code: Select all

a) [123][123][123]
b) [123][123][12]
c) [123][13][12]
d) [23][13][12]

Plus a degenerate case that contains a NAKED PAIR:

Code: Select all

e) [12][12][13]

In each case, the three cells are in the same row, column or box.
In each case, there are EXACTLY three cells that share EXACTLY three candidates.

No matter how these three cells are filled, each of the three digits will be used once and therefore can be eliminated from the other six cells in the row, column or box.

The fact that the three cells you pointed out...

Code: Select all

[157][1578][134578]

... each contain the candidates 1, 5 and 7 is a red herring. This is obvious if you consider the following three cells:

Code: Select all

[123456789][123456789][123456789]

Each cell can contain ANY digit -- nothing has been excluded yet. Any three digits you pick appear in each cell as a candidate.

[Doyle]

157 is not a valid triple, as Paul said, but 578 does make a valid (hidden) triple: 5, 7 and 8 can only be in three cells. You can remove all other numbers from those three cells, and doing so tells you where the 3 goes. It's a little easier to see the naked 146 triple, but both result in the same placement of the 3.

With naked triples, you remove those three numbers from all other cells. With hidden triples you remove all other numbers from those three cells. Just a different way of going at it.

[emm]

very nicely put

[McNessa]

Wow! I'm overwhelmed by the responses. I now know what to look for in "Naked" and "Hidden" triples.

Thanks everyone!

[cheesemeister]

I'm not sure how to figure out which if either of the two potentials is a true triple from this grouping:
{12}{14}{1248}{148}
when i started making this post I was leaning towards 124 being a triple now i'm thinking its actually a quad tho that doesnt help much since theyr spread across three boxes and all the other squares in the row are assigned.
any other thoughts?
cheese

[PaulIQ164]

Yeah, there isn't anything there except the trivial quad. Notice that you can fill those cells more than one way at the moment: 1,4,2,8; 2,4,8,1 etc. If there were a triple, you'd be able to fix the remaining cell.