The New Sudoku Players' Forum

[Leren]

Code: Select all

*-----------*
|..4|..9|..2|
|.8.|1..|.4.|
|1..|.3.|7..|
|---+---+---|
|4..|.1.|.7.|
|..7|5..|6..|
|.5.|..3|..8|
|---+---+---|
|3..|.51|...|
|...|...|...|
|...|.28|..6|
*-----------*
..4..9..2.8.1...4.1...3.7..4...1..7...75..6...5...3..83...51................28..6

[Cenoman]

Code: Select all

 +----------------------+--------------------+----------------------+
 |  5    3      4       |  7      8    9     |  1       6      2    |
 |  7    8      29      |  1      6    25    |  59      4      3    |
 |  1    269    269     |  24     3    245   |  7       8      59   |
 +----------------------+--------------------+----------------------+
 |  4    29     3       |  8      1    6     |  259     7      59   |
 |  8    129    7       |  5      49   24    |  6       3      14   |
 |  26   5      1269    |  249    7    3     |  249     129    8    |
 +----------------------+--------------------+----------------------+
 |  3    246    268     |  469    5    1     |  2489    29     7    |
 |  26   1246  c12568   | d3469   9-4  7     | c23489  b1259  a14   |
 |  9    7      15      | e34     2    8     |  34     a15     6    |
 +----------------------+--------------------+----------------------+

(4=15)b9p68 - r8c8 = (5-83)r8c37 = r8c4 - (3=4)r9c4 => -4 r8c5; ste

[Mauriès Robert]

Hi all,
My resolution with an anti-track:
P'(1r6c3) : -1r6c3->269r236c3->8r7c3->8r8c7->3r9c7->(4r9c4->2r3c4)->9r6c4->9r5c2
=> -1r5c2, stte.


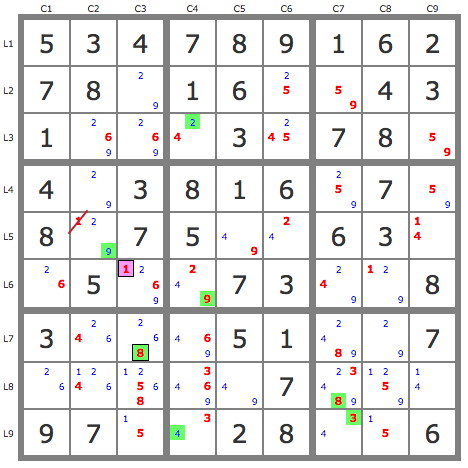
Robert

[Ngisa]

Code: Select all

+-----------------------+---------------------+-----------------------+
| 5      3        4     | 7        8      9   | 1         6        2  |
| 7      8        29    | 1        6      25  | 59        4        3  |
| 1      269      269   | 24       3      245 | 7         8        59 |
+-----------------------+---------------------+-----------------------+
| 4      29       3     | 8        1      6   | 259       7        59 |
| 8      129      7     | 5        49     24  | 6         3       h14 |
| 26     5        1269  | 29-4     7      3   |i249      g129      8  |
+-----------------------+---------------------+-----------------------+
| 3      246      268   | 469      5      1   | 2489      29       7  |
| 26     1246    d12568 | 3469     49     7   |c23489     1259     14 |
| 9      7       e15    |a34       2      8   |b34       f15       6  |
+-----------------------+---------------------+-----------------------+


(4=3)r9c4 - r9c7 = (3-8)r8c7 = (8-5)r8c3 = r9c3 - (5=1)r9c8 - r6c8 = (1-4)r5c9 = (4)r6c7 => - 4r6c4; stte

Clement

[SteveG48]

Code: Select all

 *--------------------------------------------------------------------*
 | 5      3      4      | 7      8      9      | 1      6      2      |
 | 7      8      29     | 1      6      25     | 59     4      3      |
 | 1      269    269    | 24     3      245    | 7      8      59     |
 *----------------------+----------------------+----------------------|
 | 4      29     3      | 8      1      6      | 259    7      59     |
 | 8      129    7      | 5      49     24     | 6      3      14     |
 | 26     5      1269   | 249    7      3      | 249    129    8      |
 *----------------------+----------------------+----------------------|
 | 3      246    268    | 469    5      1      | 2489   29     7      |
 | 26     1246  c12568  |b369-4  9-4    7      |c23489 c1259  d14     |
 | 9      7      15     |a34     2      8      | 3-4   d15     6      |
 *--------------------------------------------------------------------*


(4=3)r9c4 - 3r8c4 = (385)r8c738 - (5=14)b9p68 => -4 r8c45,r9c7 ; stte

Hmm. Basically the same as Cenoman.

[Mauriès Robert]

Hi all,
Small exercise to write different proposed solutions, but with TDP :
Cenoman
P'(4r8c9) : -4r8c9->1r8c9->5r8c9->5r8c3->8r8c7->3r8c4->4r9c4 =>-4r8c45.
Clement
P'(4r9c4) : -4r9c4->3r9c4->3r8c7->8r8c3->5r9c3->1r9c8->1r5c9->4r6c7 =>-4r6c4.
Steve
P'(4r9c4) : -4r9c4->3r9c4->(3r8c7->8r8c3->5r8c8)->1r9c8->4r8c9 =>-4r8c45,r9c7
I note that these are all chains of contradiction, including that of my resolution.
By the way, how would you write my resolution with an AIC?
Cordially
Robert

[Cenoman]

Hi Robert,
In a recent past, SpAce would have already delivered his Eureka teaching to you !
I am not as good a teacher as he is. So bad for you...

P'(1r6c3) : -1r6c3->269r236c3->8r7c3->8r8c7->3r9c7->(4r9c4->2r3c4)->9r6c4->9r5c2
=> -1r5c2, stte.

Term to term, the following AIC is equivalent to your diagram (see coloured digits, all on the right side of the strong link symbol "=") :
(1=926)r236c3 - (2|6=8)r7c3 - r7c7 = (8-3)r8c7 = 3r9c7 - (3=42)r39c4 - (2|4=9)r6c4 - r5c5 = (9)r5c2 => -1 r5c2
Some nodes could be merged:
(1=9268)r2367c3 - r7c7 = (83)r89c7 - (3=429)r369c4 - r5c5 = (9)r5c2 => -1 r5c2

Rather than the cumbersome ALS's in c3, I'd rather use the (15)r89c3 almost hidden pair, to the lighter AIC:
(1)r6c3 = (15-8)r89c3 = (83)r89c7 - (3=429)r369c4 - r5c5 = (9)r5c2 => -1 r5c2
but I don't know whether using AHS's is foreseen in TDP.

[pjb]

Code: Select all

 5       3       4      | 7      8      9      | 1       6      2     
 7       8       29     | 1      6      25     | 59      4      3     
 1       269     269    | 24     3      245    | 7       8      59     
------------------------+----------------------+---------------------
 4       29      3      | 8      1      6      | 259     7      59     
 8       129     7      | 5      49     24     | 6       3      14     
 26      5       1269   | 249    7      3      | 249     129    8     
------------------------+----------------------+---------------------
 3       246     268    | 469    5      1      | 2489    29     7     
 26      1246   c12568  |a3469   49     7      |b2489-3 d1259  f14     
 9       7       15     | 34     2      8      |g43     e15     6     


(3)r8c4 = (3-8)r8c7 = (8-5)r8c3 = r8c8 - (5=1)r9c8 - (1=4)r8c9 - (4=3)r9c7 => -3 r8c7, r9c4; stte

Phil

[Mauriès Robert]

Hi Cenoman, and thank you for explaining it as clearly as SpAce could.
Vous écrivez :

Rather than the cumbersome ALS's in c3, I'd rather use the (15)r89c3 almost hidden pair, to the lighter AIC:
(1)r6c3 = (15-8)r89c3 = (83)r89c7 - (3=429)r369c4 - r5c5 = (9)r5c2 => -1 r5c2
but I don't know whether using AHS's is foreseen in TDP.

Yes the ALS and AHS can be used with TDP, for example the equivalent of your AIC could be written :
P'(1r6c3): -1r6c3->15r89c3->83r89c7->429r369c4->9r5c2
But this may not be understood, whereas it would usually be written as follows:
P'(1r6c3) : -1r6c3->15r89c3->(8r8c7->3r9c7)->(4r9c4->2r3c4->9r6c4)->9r5c2 more explicit with or without the ().
Yours sincerely
Robert