The New Sudoku Players' Forum

[Mauriès Robert]

Murphy's Law is a famous reflection made by Edward Aloysius Murphy Jr., an American aerospace engineer, to one of his collaborators during an experiment carried out in 1949 and failed because of him: "If this guy has the slightest chance of making a mistake, he'll make it". It is stated today in the following concise form: "Anything that can go wrong, will go wrong".
Murphy's law, we should say Murphy's pseudo-law, is not a law in the scientific sense of the word, because it is not always true and has no scientific basis. It can barely be given a probabilistic meaning, and it is this interpretation of Murphy's Law that should be retained for Sudoku in the application of the tracks technique, namely :

A track or anti-track that develops easily has a great chance of running into a contradiction before covering the whole puzzle!

Although this is often true, it is not an established principle, as there are also many examples where an arbitrary choice leads to a solution (backdoor) or a dead end.
Nevertheless, Murphy's Law can be summarized in this way as an aid to decision making or, in other words, as an "intelligent" use of T&E.

Effectiveness of Murphy's Law
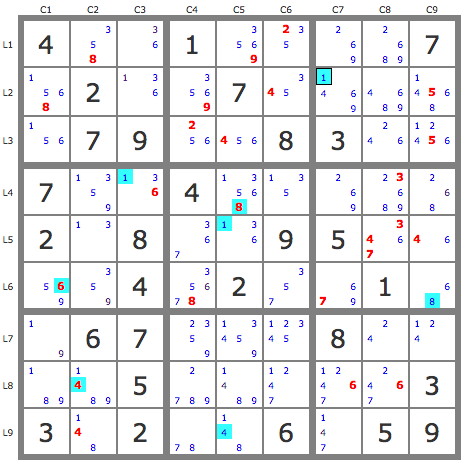
Here is an example to illustrate this point.
The observation of this puzzle shows that if the 1 of L2C7 is not a solution, then appears in block 3 the naked-pair 1/5 (hidden pair) which allows to eliminate several candidates in this block and in the puzzle.
It is therefore advisable to verify this conjecture, as it is probable according to Murphy's law.
One thus studies a track at the beginning of the 1 of L2C7 which indeed, as it was probable, leads to a contradiction with no possible 4 on C7 (see puzzle).

P(1r2c7) : 1r2c7->1r4c3->(6r6c1&1r5c5*)->8r6c9->8r4c5*->4r9c5->4r8c2->contradiction => -1r2c7.



It would be interesting, if it is not already done, to build a specific program whose purpose would be to determine on a large number of puzzles, the percentage of candidates of a puzzle that lead to a contradiction according to the level of the puzzle, and thus to give a little more foundation to Murphy's Law.
Robert

[eleven]

It is an old question, when puzzles cannot be solved with one's arsenal of solving techniques, if something like "advised guesses" can be found. To my knowledge there was never a satisfying answer.

(Btw the sample is not a good choice for me, because it can be solved with skyscrapers and wings, which will be found directly with some practice.)

Before we try to get (arbitrary) statistical results, we should precise and define in some way, what we are looking for.
If you are stuck with a grid of say 120 candidates, it is easy for a program to "try" them all, but stupid for a manual solver. Some advanced solvers now will try to find nets instead of chains, others "almost" or exotic patterns.
In any case no one will make a big effort to eliminate a candidate, which does not make some progress like solving a cell or more.

So the first step would be to select potential candidates like the ones from bivalue/bilocation cells. Robert's choice here was already more sophisticated, because only after applying pairs it turns out, that the elimination is really useful. Here i wonder, why he selected that one - the skyscraper 7 gives at least 3 singles, and why not try 1r5c2, which solves the puzzle with a pair ?

Only if we have defined an order, which candidates should be tried (and we can quickly forget the ones, where we are stuck again soon), we can check, which probability we have either to solve the puzzle luckily or eliminate a candidate with predefined techniques (e.g. singles or basics).

[Mauriès Robert]

Hi Eleven,
In the example I have chosen, the purpose is only to illustrate my point about an "intelligent" choice of a candidate to be eliminated based on Murphy's Law, and not to solve the grid that other methods allow. Thus I have not drawn attention to the skyscrapers of the 7, which can be used before or after (confluence property) to finish the resolution. This choice of 1r2c7 is not the only interesting one to make obviously.
I agree with you to say that if one envisages to study the consequences of a test on a candidate, this must be done with the aim of obtaining an effective result and not only the possible elimination of this only candidate.
Sincerely
Robert

[Ajò Dimonios]

Hi Robert.

It is clear that not all possible eliminations have the same importance, while some targeted ones produce a decisive effect such as the elimination of candidate r2c7 = 1 or candidate r7c9 = 1 or r4c3 = 1 which solve the scheme. This particular scheme has a very particular characteristic, 23 candidates 1 out of 24, if they are true, produce a track that is either invalid or is a backdoor. The only track that does not produce any results is P (1r5c5).It can be calculated that a random choice of one of the 24 candidates 1 produces a useful result with a percentage of 23 * 100/24 = 95.83%, of which since there are 7 backdoors with candidate 1 (one for each block) a percentage of 7 * 100/24 = 29.16% is obtained to obtain a backdoor and the remaining 66.67% to obtain an invalid tracks, of which 3 * 100/24 = 12.5% lead to the solution with a single step .

Paolo

[dxSudoku]

I like the idea of "Negative Murphy's Law". Negative Murphy's law is extremely powerful magic. The way it works is the things you think about that may happen are the things that don't happen. I don't know how it applies to solving Sudoku puzzles. But I do know if I go to a store and put the receipt in my wallet, then I will never need it. Anytime I lose the receipt, this is the time I have purchased a defective product. It's amazing how this works!