The New Sudoku Players' Forum

[mith]

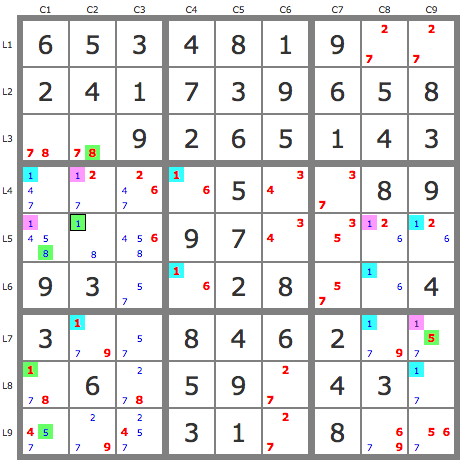
Code: Select all

+-------+-------+-------+
| . . 3 | . . 1 | . . . |
| . 4 1 | . . . | . 5 . |
| . . 9 | 2 6 5 | . . 3 |
+-------+-------+-------+
| . . . | . 5 . | . 8 9 |
| . . . | . 7 . | . . . |
| 9 3 . | . 2 . | . . . |
+-------+-------+-------+
| 3 . . | 8 4 6 | 2 . . |
| . 6 . | . . . | 4 3 . |
| . . . | 3 . . | 8 . . |
+-------+-------+-------+
..3..1....41....5...9265..3....5..89....7....93..2....3..8462...6....43....3..8..

[Cenoman]

Not found a reasonable one-step solution, so two steps:

Code: Select all

 +---------------------+-----------------+-------------------+
 |  6      5     3     |  4    8    1    |  9    27    27    |
 |  2      4     1     |  7    3    9    |  6    5     8     |
 | e78    d78    9     |  2    6    5    |  1    4     3     |
 +---------------------+-----------------+-------------------+
 |  147    127   246   |  16   5    34   |  37   8     9     |
 |  1458  c18    468   |  9    7    34   |  35   126   126   |
 |  9      3     57    |  16   2    8    |  57   16    4     |
 +---------------------+-----------------+-------------------+
 |  3     b179   57    |  8    4    6    |  2    179   157   |
 | a17-8   6     28    |  5    9    27   |  4    3     17    |
 |  457    279   24    |  3    1    27   |  8    679   567   |
 +---------------------+-----------------+-------------------+

1. S-Wing (1)r8c1 = r7c2 - (1=8)r5c2 - r3c2 = (8)r3c1 => -8 r8c1; 3 placements & basics

Code: Select all

 +---------------------+-----------------+-------------------+
 |  6      5     3     |  4    8    1    |  9    27    27    |
 |  2      4     1     |  7    3    9    |  6    5     8     |
 |  78     78    9     |  2    6    5    |  1    4     3     |
 +---------------------+-----------------+-------------------+
 |  147    127   246   |  16   5    34   |  37   8     9     |
 | c1458   18    6-4   |  9    7   a34   | b35   126   126   |
 |  9      3     57    |  16   2    8    |  57   16    4     |
 +---------------------+-----------------+-------------------+
 |  3      179   57    |  8    4    6    |  2    179   157   |
 |  17     6     8     |  5    9    2    |  4    3     17    |
 | d45     29   e24    |  3    1    7    |  8    69    56    |
 +---------------------+-----------------+-------------------+

2. (4=3)r5c6 - (3=5)r5c7 - r5c1 = (5-4)r9c1 = (4)r9c3 => -4 r5c3; ste

Since oddagons are fashionable, an (ugly) alternative step 2:

Hidden Text: Show

The first proposed oddagon was not correctly used (one forgotten guardian)
Thanks to Robert Mauriès for spotting..
Another one, hopefully correct

Code: Select all

 +----------------------+-----------------+-------------------+
 |  6       5     3     |  4    8    1    |  9    27    27    |
 |  2       4     1     |  7    3    9    |  6    5     8     |
 |  78      78    9     |  2    6    5    |  1    4     3     |
 +----------------------+-----------------+-------------------+
 | B147    a127#  246   |  16   5    34   |  37   8     9     |
 | b1458#  b18*   6-4   |  9    7  zb34   |zb35  a126# C126*  |
 |  9       3    x57    |  16   2    8    | y57   16    4     |
 +----------------------+-----------------+-------------------+
 |  3       179* w57    |  8    4    6    |  2    179  v157#  |
 | B17*     6     8     |  5    9    2    |  4    3     17*   |
 | y45      29    24    |  3    1    7    |  8    69   x56    |
 +----------------------+-----------------+-------------------+

5-link oddagon r58, c29, b7 (*) having four guardians (#)
(1)r4c2,r5c8 - (1=3584)r5c1267
(1)r5c1 - (1=74)r48c1
(1-5)r7c9 = r7c3 - r6c3 = r6c7 - (5=34)r5c67
=> -4 r5c3; ste

[denis_berthier]

Since oddagons are fashionable, an (ugly) alternative step 2:
[...]

Hidden Text: Show

7-link oddagon (1)r467, c249, b6 having four guardians (#)
(1)r57c8 - (1=6)r6c8
(1-8)r5c2 = (8-5)r5c1 = r9c1 - (5=6)r9c9
(1)r4c1 - r4c4 = r6c4 - (1=6)r6c8
=> -6 r5c9, r9c8; ste

I have a trivial solution with bivalue-chains[≤3], but I tried to activate only oddagons (and Subsets). It's not enough to solve the puzzle, but I find two:

Hidden Text: Show

***********************************************************************************************
*** SudoRules 20.1.s based on CSP-Rules 2.1.s, config = O+S
*** Using CLIPS 6.32-r773
***********************************************************************************************
lots of singles
124 candidates, 481 csp-links and 481 links. Density = 6.31%
whip[1]: c7n7{r6 .} ==> r6c9 ≠ 7, r6c8 ≠ 7
whip[1]: c7n5{r6 .} ==> r6c9 ≠ 5, r5c9 ≠ 5
whip[1]: r4n2{c3 .} ==> r5c3 ≠ 2, r5c2 ≠ 2
naked-pairs-in-a-row: r6{c4 c8}{n1 n6} ==> r6c9 ≠ 6, r6c9 ≠ 1, r6c3 ≠ 6
singles ==> r6c9 = 4, r6c6 = 8
naked-pairs-in-a-column: c3{r6 r7}{n5 n7} ==> r9c3 ≠ 7, r9c3 ≠ 5, r8c3 ≠ 7, r5c3 ≠ 5, r4c3 ≠ 7
oddagon[7]: r7c2{n1 n9},r7n9{c2 c8},r7c8{n9 n7},b9n7{r7c8 r8c9},r8c9{n7 n1},r8n1{c9 c1},b7n1{r8c1 r7c2} ==> r7c8 ≠ 7
oddagon[9]: b7n1{r7c2 r8c1},r8n1{c1 c9},r8c9{n1 n7},b9n7{r8c9 r7c9},r7n7{c9 c2},c2n7{r7 r9},r9c2{n7 n9},c2n9{r9 r7},r7c2{n9 n1} ==> r9c2 ≠ 7
at this point, more rules are needed.

[Mauriès Robert]

Hi all,
Here's a two-step resolution, the first of which uses an oddagon for fun.
Step1
Oddagon[9]: guardians 1b4p24, 1r5c8,1r7c9 - loop 1b4p15, 1b5p17, 1b6p68,1 b9p26, 1r7c28 (see puzzle)
=> -1r5c2 since 1r5c2->(8r3c2 and 1r8c1)->8r5c1->5r9c1->5r7c9 and that consequently none of the guardians would be a solution.
So r5c2=8 and 5 placements.

puzzle: Show

Step2
P'(6r1c8) : (-6r6c8)=> 1r6c8->1r4c4->1r5c1->5r9c1->6r9c9 => -6r5c9, stte.
Of course, we can make it simpler.
Robert

[DEFISE]

Oddagon[9]: guardians 1b4p24, 1r5c8,1r7c9 - loop 1b4p15, 1b5p17, 1b6p68,1 b9p26, 1r7c28 (see puzzle)
=> -1r5c2 since 1r5c2->(8r3c2 and 1r8c1)->8r5c1->5r9c1->5r7c9 and that consequently none of the guardians would be a solution.

I have just understood on this example what the guardians are. Thank's !
I admit that I did not have the courage to read the literature on the subject.
However, I prefer to limit guardians to candidates who see the target.

[Mauriès Robert]

Hi François,

Oddagon[9]: guardians 1b4p24, 1r5c8,1r7c9 - loop 1b4p15, 1b5p17, 1b6p68,1 b9p26, 1r7c28 (see puzzle)
=> -1r5c2 since 1r5c2->(8r3c2 and 1r8c1)->8r5c1->5r9c1->5r7c9 and that consequently none of the guardians would be a solution.

I have just understood on this example what the guardians are. Thank's !
I admit that I did not have the courage to read the literature on the subject.
However, I prefer to limit guardians to candidates who see the target.

Take the time to read the article in Allan Barker (here) dedicated to the subject, it is quite short and very explicit.
I spent some time on the subject, because the oddagon is a way to find unusual conjugated leads issued from the guardians. Indeed, if E is the set of guardians P'(E) is invalid and therefore the tracks coming from a score of E are conjugated as we know.
If one wishes to limit oneself to oddagons whose guardians see the target, why not, but then one might as well limit the number of guardians as much as possible rather than consider all the z-candidates as guardians in order to make the best use of this property of the antipists. This makes it possible to eliminate the target but also other candidates.
Friendly.
Robert

[DEFISE]

Hi François,
Take the time to read the article in Allan Barker (here) dedicated to the subject, it is quite short and very explicit.
...

Hi Robert, maybe but later because I'm late on a lot of other personal matters.