The New Sudoku Players' Forum

[The Robman]

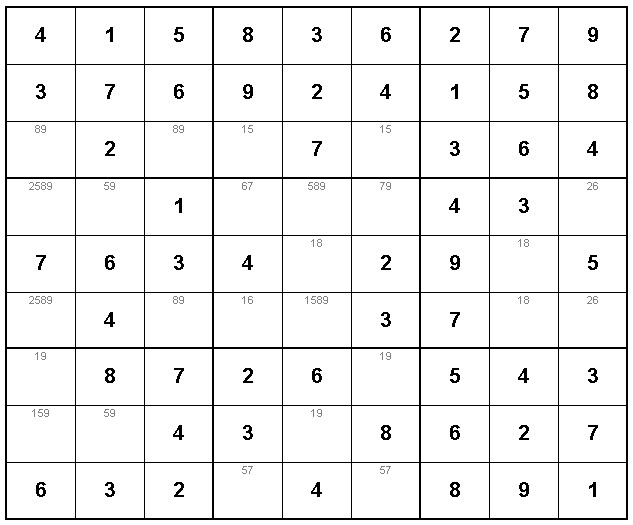
This puzzle comes from the free ad circular that arrives in your mailbox (July 27th, I think). I can solve it if I make a guess, but I want to know if there's a way to solve it without guessing.

[TKiel]

Multi-colouring on 9's:

Code: Select all

 *-----------------------------------------------------------*
 | 4     1     5     | 8     3     6     | 2     7     9     |
 | 3     7     6     | 9     2     4     | 1     5     8     |
 | 89    2     89    | 15    7     15    | 3     6     4     |
 |-------------------+-------------------+-------------------|
 | 2589  59A   1     | 67    589   79B   | 4     3     26    |
 | 7     6     3     | 4     18    2     | 9     18    5     |
 | 2589  4     89    | 16    1589  3     | 7     18    26    |
 |-------------------+-------------------+-------------------|
 | 19    8     7     | 2     6     19b   | 5     4     3     |
 | 159   59a   4     | 3     (19)  8     | 6     2     7     |
 | 6     3     2     | 57    4     57    | 8     9     1     |
 *-----------------------------------------------------------*


Since (A) and (B) both can't be 9, either (a) or (b) must be 9, so r8c5 must be 1.

[Sped]

Code: Select all

 
 *-----------------------------------------------------------*
 | 4     1     5     | 8     3     6     | 2     7     9     |
 | 3     7     6     | 9     2     4     | 1     5     8     |
 | 89    2     89    | 15    7     15    | 3     6     4     |
 |-------------------+-------------------+-------------------|
 | 2589  59^   1     | 67^   589   79^   | 4     3     26    |
 | 7     6     3     | 4    (1)8   2     | 9     18    5     |
 | 2589  4     89    | 16*  (1)589 3     | 7     18    26    |
 |-------------------+-------------------+-------------------|
 | 19^   8     7     | 2     6     19^   | 5     4     3     |
 | 159   59^   4     | 3     19*   8     | 6     2     7     |
 | 6     3     2     | 57    4     57    | 8     9     1     |
 *-----------------------------------------------------------*


An alternate solution is the xy chain:

1-(r6c4)-6-(r4c4)-7-(r4c6)-9-(r4c2)-5-(r8c2)-9-(r7c1)-1-(r7c6)-9-(r8c5)-1

which eliminates the 1s in r5c5 and r6c5, reducing the puzzle to singles.

Above, the ends of the chain are marked with *, the other cells in the chain are marked with ^, and the candidates to be excluded have () around them.

In nice loop notation:

[r56c5]-1-[r6c4]-6-[r4c4]-7-[r4c6]-9-[r4c2]-5-[r8c2]-9-[r7c1]-1-[r7c6]-9-[r8c5]-1-[r56c5] =>r56c5<>1

[The Robman]

Thanks guys. TKiel, I totally follow that, nice & easy, but I guess the trick is learning how to spot these. Sped, I'm going to have to try and study your solution for a bit to see if I can follow it.

[Sped]

Sped, I'm going to have to try and study your solution for a bit to see if I can follow it.

On second glance, the chain I noted above can be made shorter:

1-(r6c4)-6-(r4c4)-7-(r4c6)-9-(r4c2)-5-(r8c2)-9-(r8c5)-1

Code: Select all

 *-----------------------------------------------------------*
 | 4     1     5     | 8     3     6     | 2     7     9     |
 | 3     7     6     | 9     2     4     | 1     5     8     |
 | 89    2     89    | 15    7     15    | 3     6     4     |
 |-------------------+-------------------+-------------------|
 | 2589  59^   1     | 67^   589   79^   | 4     3     26    |
 | 7     6     3     | 4    (1)8   2     | 9     18    5     |
 | 2589  4     89    | 16*  (1)589 3     | 7     18    26    |
 |-------------------+-------------------+-------------------|
 | 19    8     7     | 2     6     19    | 5     4     3     |
 | 159   59^   4     | 3     19*   8     | 6     2     7     |
 | 6     3     2     | 57    4     57    | 8     9     1     |
 *-----------------------------------------------------------*


The xy chain works like this..

Either the start of the chain in r6c4 or the end of the chain in r8c5 has to be a 1. Therefore cells that see both r6c4 and r8c5 cannot be 1.

All the cells in the chain are bivalue. Pick any cell in the chain, set it to one of its two values, and follow the implications down the chain. One of the ends will be a 1. Set that cell to its other possible value and follow the implications down the chain. A 1 will appear at the other end.

Example:

r4c6 can be 7 or 9. Let's assume it's a 7. That means that r4c4 cannot be 7, it must be 6. If r4c4 is a 6, then r6c4 cannot be a 6, it must be a 1.

If r4c6 is a 7, r6c4 is forced to 1.

If we assume that r4c6 is a 9, then r4c2 cannot be a 9. It must be a 5. If r4c2 is a 5, r8c2 cannot be a 5, it must be a 9. If r8c2 is a 9, then r8c5 cannot be a 9. It must be a 1.

If r4c6 is a 9, r8c5 is forced to 1.


Any way you slice it, it's guaranteed that r6c4 or r8c5 is a 1.

Therefore r5c5 and r6c5, which see both r6c4 and r8c5, cannot possibly be 1.

[TKiel]

...but I guess the trick is learning how to spot these.

Look for strong links (conjugate links, if you prefer). Label (colour) that chain. Sometimes it's only going to be two cells long, other times it may be longer. (Three cell chains never seem to do much.) Then look for other strong links that connect somehow with the first chain. A cell from each chain that is in the same box, row or column. Both of those can't be true, so at least one of the opposite labeled cells in each chain must be true. Look for a cell that 'sees' both opposite labeled cells. Eliminate the candidate from that cell.

You'll find that you look at lots of strong links that don't do anything, mostly because there won't be a link or if there is a link, because the cell from which the candidate could be excluded is already solved or doesn't contain the candidate.

There are plenty of threads in the 'Advance solving techniques' forum about strong links (aka colouring). Multi-colouring is using two seperate chains of the same number. It's also possible to use three seperate chains. Good luck.

I thought Sped's explanation of the logic behind the chain was very good, but I would add one more thing. If you are familiar with the logic of an XY-wing, it may help to think of an XY-chain as a longer (not limited to three cells) version of that.

Tracy

[The Robman]

Thanks again to both of you for all your help. I do follow the chain stuff now.