The New Sudoku Players' Forum

Website · by **denis_berthier** » Mon Nov 30, 2020 3:32 am

DEFISE wrote:
denis_berthier wrote:3...9...4.4.5.2.3...6...9...3..5..4.1..3.6..8.6..1..7...7...4...5.1.8.2.2...4...5
The challenge here is not to solve the puzzle, but to find long oddagons.

Here is a resolution with whips and 3 oddagons

Hi DEFISE

It's strange that you find Oddagons with whips activated. SudoRules finds a solution in W4 (leaving no chance for any oddagon):

Hidden Text: Show

In order to find Oddagons, I have to activate only them + bivalue-chains.

by **Mauriès Robert** » Mon Nov 30, 2020 10:12 am

Hi François and Denis,
I studied Francois' resolution up to the first Oddagon [15] announced. For me it is not an Oddagon (Broken wing) but a whip. Indeed, the Oddagon is characterized by the fact that the invalid loop appears only if the guardians are eliminated, which is not the case here, the described loop being invalid without deletion of any guardian, thus without the use of the 8r9c3 target.
I did not check the two others, but if the same principle was applied it is not Oddagons either.
Robert

by **DEFISE** » Mon Nov 30, 2020 11:03 am

Hi Robert,
Apparently there is a big controversy over the definition of Oddagon.
For my part I was content to read the 3 examples of Denis by following the link
a-revival-of-broken-wings-t5225-91.html. (Page 7).
And I was inspired by his examples. No need to read anything else. No Broken-Wings, no guardians etc…).

by **DEFISE** » Mon Nov 30, 2020 11:56 am

denis_berthier wrote:Hi DEFISE
It's strange that you find Oddagons with whips activated. SudoRules finds a solution in W4 (leaving no chance for any oddagon):
In order to find Oddagons, I have to activate only them + bivalue-chains.

Hi Denis,
It must depend on the order of the different searches.
In my initial "Simple first" program I just inserted the search for oddagons between the search for basics and the search for whips.

Website · by **denis_berthier** » Mon Nov 30, 2020 1:30 pm

DEFISE wrote:
denis_berthier wrote:Hi DEFISE
It's strange that you find Oddagons with whips activated. SudoRules finds a solution in W4 (leaving no chance for any oddagon):
In order to find Oddagons, I have to activate only them + bivalue-chains.

Hi Denis,
It must depend on the order of the different searches.
In my initial "Simple first" program I just inserted the search for oddagons between the search for basics and the search for whips.

I see.
In SudoRules, oddagons follow the same priority rules as the other patterns: oddagons[n] are at level n.
Oddagons are a generic pattern, but an exotic one. Oddagons[n] are therefore just before all the generic non-exotic patterns of length n.

Anyway, you get the cup for the longest ones. Those I found have lengths ≤ 11.

by **Mauriès Robert** » Mon Nov 30, 2020 5:49 pm

Hi Denis,
You did not answer my comment that I remind :

Mauriès Robert wrote:I studied Francois' resolution up to the first Oddagon [15] announced. For me it is not an Oddagon (Broken wing) but a whip. Indeed, the Oddagon is characterized by the fact that the invalid loop appears only if the guardians are eliminated, which is not the case here, the described loop being invalid without deletion of any guardian, thus without the use of the 8r9c3 target.
I did not check the two others, but if the same principle was applied it is not Oddagons either.

Am I right or wrong ?
Robert

Website · by **denis_berthier** » Mon Nov 30, 2020 6:20 pm

Mauriès Robert wrote:You did not answer my comment that I remind :
Mauriès Robert wrote:I studied Francois' resolution up to the first Oddagon [15] announced. For me it is not an Oddagon (Broken wing) but a whip. Indeed, the Oddagon is characterized by the fact that the invalid loop appears only if the guardians are eliminated, which is not the case here, the described loop being invalid without deletion of any guardian, thus without the use of the 8r9c3 target.
I did not check the two others, but if the same principle was applied it is not Oddagons either.

Am I right or wrong ?

I hadn't seen it. Guardians are z-candidates; they are not eliminated.
In oddagon[n]: {a1 a2},{a2 a3}, ...,{an a1} => not Z, the logic is very simple (because there is an odd number of bivalue (modulo Z) cells:

Code: Select all: if Z then a1 => not a2 => a3 => not a4 =>.... => not a1 not a1 => a2 => not a3 => a4 => ... => a1

by **Mauriès Robert** » Mon Nov 30, 2020 6:33 pm

So according to you, the oddagon [15] described by François is indeed an oddagon?
Robert

by **DEFISE** » Mon Nov 30, 2020 8:47 pm

Hi Robert,
Oddagon or not Oddagon this logic works and that’s all that matters to me. My eliminations are justified. There may be other more general patterns that work as well, but this one has the merit of simplicity.

by **Mauriès Robert** » Mon Nov 30, 2020 9:35 pm

Hi François,
Yes your reasoning works, it corresponds to the scheme described in the last post above from Denis answering me. Your elimination is correct. I have only made a bad connection between Denis' conception of the oddagon and the one (original concept) that I read based on the notion of guardians which seems to me to be broader.
The loop [15] that you construct corresponds to an oddagon (original concept) whose keepers are 3r9c3 and 8r9c8, whereas Denis considers that the keepers are all the z-candidates who see the 8r9c3 target, which is restrictive in my opinion. Indeed, with Denis's design, only 8r9c3 is eliminated, whereas with the original design 8r9c3 is eliminated but all the candidates common to the tracks from 3r9c3 and 8r9c8 can be validated since these tracks are conjugated, so for example r7c9=3, stte (see puzzle).

puzzle: Show

In any case, congratulations for having found this loop[15].
Robert

Website · by **denis_berthier** » Tue Dec 01, 2020 6:21 am

Hi Robert
If you want to learn more about oddagons, you'd better follow the link already given by DEFISE: http://forum.enjoysudoku.com/a-revival-of-broken-wings-t5225-91.html. Whether and how they are related to previously defined patterns (such as broken wing) is irrelevant.

Website · by **denis_berthier** » Tue Dec 01, 2020 6:48 am

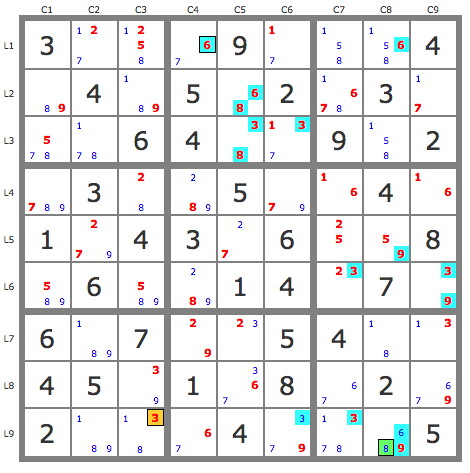
Let me now give my solution with oddagons and explain how I found it.

As I've shown before, this puzzle is in W4. I therefore decided to try to solve it without whips. The first natural choice is to use only reversible patterns. (Another possibility would be to use only 2D chains.)

I first tried to activate all the reversible patterns in SudoRules: Subsets (Naked, Hidden and Super-Hidden), bivalue-chains, z-chains and oddagons, as shown in the following options of the SudoRules configuration file:

Code: Select all: (bind ?*Subsets* TRUE) (bind ?*Bivalue-Chains* TRUE) (bind ?*z-Chains* TRUE) (bind ?*Oddagons* TRUE)

It appeared that this puzzle is also in Z4:

Hidden Text: Show

This is probably the simplest solution one can hope, in terms of patterns involved and their maximal lengths (using only Subsets and bivalue-chains is not enough). As you can see from the resolution path, it heavily relies on z-chains.

But that day, I had set my mind on hunting oddagons. So I tried to de-activate z-chains, using the following configuration:

Code: Select all: (bind ?*Subsets* TRUE) (bind ?*Bivalue-Chains* TRUE) (bind ?*Oddagons* TRUE)

Notice that, while the previous choice was "natural", this one is less so. As oddagons rely on z-candidates, why would one activate them but not z-chains? Anyway, SudoRules allows to play freely with all the rules combinations (provided they are consistent). (What SudoRules doesn't allow easily is to change the relative priorities of rules.)

Hidden Text: Show

This is a more complex solution than with z-chains, but we got our oddagons (with max length 11), without changing the natural rules priorities.

by **Mauriès Robert** » Tue Dec 01, 2020 8:31 am

Hi Denis,

denis_berthier wrote:Hi Robert
If you want to learn more about oddagons, you'd better follow the link already given by DEFISE: http://forum.enjoysudoku.com/a-revival-of-broken-wings-t5225-91.html. Whether and how they are related to previously defined patterns (such as broken wing) is irrelevant.

I have read and reread these texts because you had already given me this link at the beginning of this thread. I think I now have a fair idea of the mostly agreed definition of an oddagon and your definition. For example, you replied to eleven that guardians are for you z-candidates (so you didn't mention them), this is a restriction that makes your definition a special case of the general definition. I too invite you to read Allan Barker's point of view http://sudoku.allanbarker.com/sweb/gen2/blacklog.htm and why not participate in the thread I created (Oddagon or not Oddagon) to explain why you think the example I give is not an oddagon.
Cordialy
Robert

Website · by **denis_berthier** » Tue Dec 01, 2020 8:40 am

Mauriès Robert wrote:I think I now have a fair idea of the mostly agreed definition of an oddagon and your definition.

There is no difference between "the mostly agreed definition of an oddagon" (which you don't even mention) and mine.
If you have any doubts, ask the expert on this topic, i.e. Tarek.

by **Mauriès Robert** » Tue Dec 01, 2020 9:24 am

denis_berthier wrote:
Mauriès Robert wrote:I think I now have a fair idea of the mostly agreed definition of an oddagon and your definition.

There is no difference between "the mostly agreed definition of an oddagon" (which you don't even mention) and mine.

I suggest you then explain in the thread "Oddagon or not Oddagon" why you consider that in SteveC's example it is not an oddagon as you told me.
As for the commonly accepted definition of the oddagon (Broken wing), I refer you to the definition of its creator RodHagglund and to the broader definition of Allan Barker among others, definitions all of which are based on the principle of guardians who are not necessarily z-candidates.
Robert
PS :I will indeed ask Tarek to arbitrate this debate.

The New Sudoku Players' Forum

Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3

Re: Lozenges 8.3