1) I focused ONLY on the cells with 2 candidates, ignoring everything else.
2) I looked for all the pairs, triples, quads, etc. and see how they connect. I think of these as "binary groups" as they can be in only one of two states. For instance, a [12][12] pair can only be 1-2 or 2-1. A quad of [12][23] [34][14] can only be 1-2-3-4 or 2-3-4-1. The cells within these groups are connected by BLUE lines here.
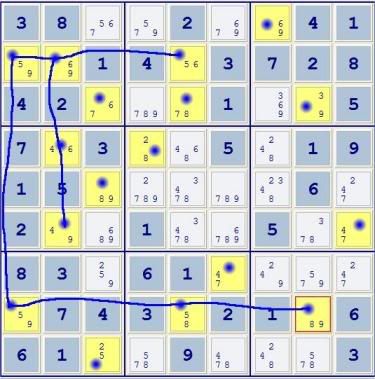
3) Now I try to form a closed loops by connecting all other cells that share candidates with with RED lines.
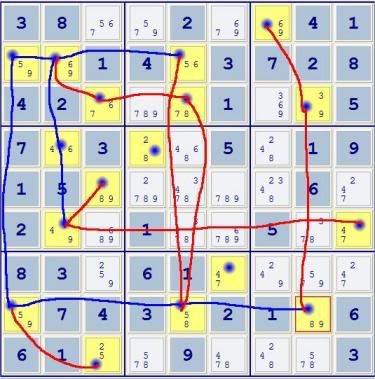
4) In order to form a pair of forcing chains, I MUST form a complete loop. So, I can simplify be removing all lines that dead end.
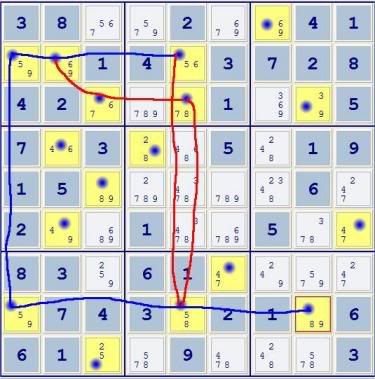
5) All cells within a binary group are internally consistent. If each cell in the chain formed is in the same binary group with then next cell, A PROOF CANNOT BE FORMED! Instead, you will have a single chain that can be in two states. For example:
Look at the triplets in rows 2 and 8. Each has candidate 5s in columns 1 and 5. Therefore, these two triplets can exist in exactly two states:
- Code: Select all
59--6
9---5--8
or
96--5
5---8--9
Therefore, they form a single 6-cell binary group, so I'll change the RED line connecting two of their cells to BLUE. #6.
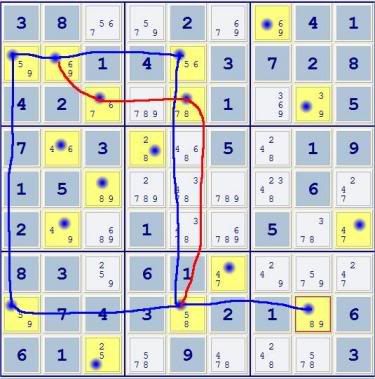
6) Because binary groups are internally consistent, you can move around blue paths all you want without and never find a contradiction or make a proof. You can see this for yourself here. Our proof MUST contain at least one red line -- in this case, there are only two closed paths including the red lines. BOTH OF THEM SOLVE THE PUZZLE! Start at EITHER cell
at the intersection of a RED and BLUE line, form two chains connected to the OTHER. One chain MUST use the RED
line, the other, either of the BLUE paths available.
Here are ALL possible results:
r2c2=6 => r3c3=7 => r3c5=8 => r8c5=5
r2c2=9 => r2c1=5 => r8c1=9 => r8c5=5
Therefore, r8c5=5
r8c5=5 => r2c5=6 => r2c2=9
r8c5=8 => r3c5=7 => r3c3=6 => r2c2=9
Therefore, r2c2=9
These are EXACTLY the chains Jeff posted above. I believe this shows not only that these forcing chains solve the puzzle, but that they are the only 'xy-chains' that do AND, that they can be found by a method that does NOT use any look-ahead, but step-by-step logic.
Loops that contain only blue lines cannot form a proof.
Loops that contain red lines, may or may not form a proof, but they may be converted to blue, thereby reducing your 'path candidates', if they can be isolated in a loop. (The line connecting r28c5 was in a loop in which it was the only red line -- that loop was shown to be internally consistant, it was converted to blue.)
I rarely draw lines like this -- I've done this here for illustration of thought process. But even if you do, and go so far as to convert red lines to blue and erase dead end chains as I've done here -- this is really only different by degree from writing in dozens and dozens of little pencil marks only to erase them later. If one is fair, both are fair. If one is logic, the other is logic.
This is the basic way that I use to find forcing chains, but can vary quite a bit depending on the particulars, and I have no compunction to try to keep the chains 'pure' -- if I see something else that helps form the chain, I'll use it.






