The New Sudoku Players' Forum

[tarek]

Code: Select all

+-------+-------+-------+
| . . . | . . . | . . . |
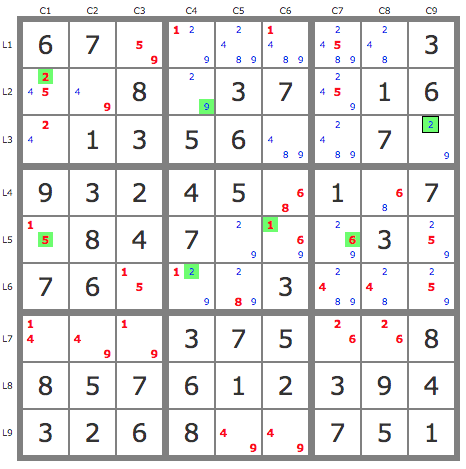
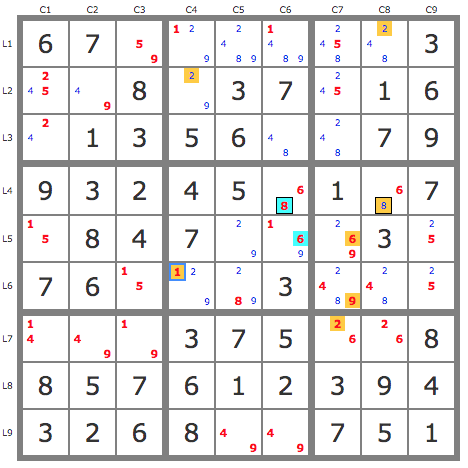
| . . 8 | . . 7 | . 1 6 |
| . 1 3 | 5 6 . | . . . |
+-------+-------+-------+
| . . 2 | 4 5 . | 1 . 7 |
| . . 4 | 7 . . | . 3 . |
| . 6 . | . . . | . . . |
+-------+-------+-------+
| . . . | 3 . . | . . 8 |
| . 5 . | . 1 . | . . 4 |
| . 2 . | 8 . . | 7 5 . |
+-------+-------+-------+
...........8..7.16.1356......245.1.7..47...3..6..........3....8.5..1...4.2.8..75.


Play this puzzle online

Download Sukaku Explainer

[Mauriès Robert]

Hi all,
A two-step resolution with TDP.

Step 1 with an anti-track :
P'(2r56c9) : -2r56c9->2r3c9-> --- ->2r6c4 and 6r5c7 (see puzzle) => -2c78b6 => r3c9=9

puzzle1: Show

Step 2 with two conjugated tracks :
P(8r4c6) : 8r4c6->6r5c6->1r6c4
P(8r4c8) : 8r4c8-> --- ->1r6c4 (see puzzle2) => r6c4=1, stte

puzzle2: Show

Robert

[Cenoman]

The most reasonable solution (to me) is in two steps

Code: Select all

 +------------------+----------------------+----------------------+
 |  6     7   c59   |  129   2489   1489   | b24589   248   3     |
 |  245  c49   8    |  29    3      7      | a259-4   1     6     |
 |  24    1    3    |  5     6      489    |  2489    7     29    |
 +------------------+----------------------+----------------------+
 |  9     3    2    |  4     5      68     |  1       68    7     |
 |  15    8    4    |  7     29     169    |  269     3     259   |
 |  7     6    15   |  129   289    3      |  2489    248   259   |
 +------------------+----------------------+----------------------+
 |  14    49   19   |  3     7      5      |  26      26    8     |
 |  8     5    7    |  6     1      2      |  3       9     4     |
 |  3     2    6    |  8     49     49     |  7       5     1     |
 +------------------+----------------------+----------------------+

1. H-wing (5)r2c7 = r1c7 - (5=94)b1p35 => -4 r2c7; two placements & basics

Code: Select all

 +-----------------+----------------------+--------------------+
 |  6    7    59   |  129   2489   1489   |  2458   248   3    |
 | c45  c49   8    | c29    3      7      |  25     1     6    |
 |  2    1    3    |  5     6      48     |  48     7     9    |
 +-----------------+----------------------+--------------------+
 |  9    3    2    |  4     5      68     |  1      68    7    |
 | d15   8    4    |  7     29    a69-1*  | a69*    3     25   |
 |  7    6    15   |ba129*  289    3      | a489*   48    25   |
 +-----------------+----------------------+--------------------+
 |  14   49   19   |  3     7      5      |  26     26    8    |
 |  8    5    7    |  6     1      2      |  3      9     4    |
 |  3    2    6    |  8     49     49     |  7      5     1    |
 +-----------------+----------------------+--------------------+

2. Almost M3-wing [(6)r5c6 = (6-9)r5c7 = r6c7 - (9=1)r6c4] = (2)r6c4 - (2=495)r2c124 - (5=1)r5c1 => -1 r5c6; ste

But a one-stepper exists, with a 5-cell kraken in the 2s

Hidden Text: Show

Kraken row (2)r6c45789
(2)r6c4 - (2=9)r2c4 - (9=245)b1p457
(2)r6c5 - (2=91)b5p57 - r6c3 = (1-5)r5c1 = (5)r2c1
(2)r6c7 - (2=6)r7c7 - r5c7 = (6-1)r5c6 = (1-5)r5c1 = (5)r2c1
(2)r6c8 - r56c9 = r3c9 - (2=4)r3c1 - r2c12 = (4)r2c7
(2-5)r6c9 = r5c9 - r5c1 = (5)r2c1
=>-5r2c7; ste

[eleven]

The most reasonable solution (to me) is in two steps

Agreed. I cannot look for a one-stepper chain here without always stumbling across the xy-wing.
Then e.g.:

Code: Select all

+-------------------+-------------------+-------------------+
| 6     7     59    | 129   2489  1489  | 2458  248   3     |
|c45   c49    8     |c29    3     7     | 245   1     6     |
| 2     1     3     | 5     6     48    | 48    7     9     |
+-------------------+-------------------+-------------------+
| 9     3     2     | 4     5     68    | 1     68    7     |
|d15    8     4     | 7    a29   a169   |a269   3    e25    |
| 7     6     15    |b129   289   3     | 2489  248   25    |
+-------------------+-------------------+-------------------+
| 14    49    19    | 3     7     5     | 26    26    8     |
| 8     5     7     | 6     1     2     | 3     9     4     |
| 3     2     6     | 8     49    49    | 7     5     1     |
+-------------------+-------------------+-------------------+

(2=619)r5c765 - (1|9=2)r6c4 - (2=495)r2c241 - r5c1 = 5r5c9 => -2r5c9, stte

[Leren]

Similar to eleven. XY Wing followed by a Kraken cell/ Death Blossom :

Code: Select all

*------------------------------------------------*
| 6      7   59 | 129   2489 1489 | 2458 248 3   |
|b45    b49  8  |b29    3    7    | 25   1   6   |
| 2      1   3  | 5     6    48   | 48   7   9   |
|---------------+-----------------+--------------|
| 9      3   2  | 4     5    68   | 1    68  7   |
|c1-5cC  8   4  | 7     29B  169  | 69   3   25B |
| 7      6  b15 |a129aA 289  3    | 489  48  25  |
|---------------+-----------------+--------------|
| 14     49  19 | 3     7    5    | 26   26  8   |
| 8      5   7  | 6     1    2    | 3    9   4   |
| 3      2   6  | 8     49   49   | 7    5   1   |
*------------------------------------------------*

1 r6c4 = (1=5) r6c3   - 5 r5c1;

2 r6c4 - (2=5) r2c124 - 5 r5c1;

9 r6c4 - (9=5) r5c59  - 5 r5c1; -=> - 5 r5c1; stte

Leren

[pjb]

Code: Select all

 6       7      c59     | 129    2489   1489   | 24589  248    3     
f245    d49      8      |e29     3      7      | 2459   1      6     
g24      1       3      | 5      6      489    | 2489   7     h29     
------------------------+----------------------+---------------------
 9       3       2      | 4      5      68     | 1      68     7     
a15      8       4      | 7     j29     69-1   | 269    3     i259   
 7       6      b5-1    |k129    289    3      | 2489   248    259   
------------------------+----------------------+---------------------
 14      49      19     | 3      7      5      | 26     26     8     
 8       5       7      | 6      1      2      | 3      9      4     
 3       2       6      | 8      49     49     | 7      5      1     


(1=5*)r5c1 - r6c3 = (5^-9)r1c3 = r2c2 - (9=2#)r2c4 - (25^=4)r2c1 - (4=2)r3c1 - (2=9)r3c9 - (5*9=2)r5c9 - (2=9)r5c5 - (2#9=1)r6c4 => -1 r5c6, r6c3; stte

Phil

[Mauriès Robert]

Hi Phil,

(1=5*)r5c1 - r6c3 = (5^-9)r1c3 = r2c2 - (9=2#)r2c4 - (25^=4)r2c1 - (4=2)r3c1 - (2=9)r3c9 - (5*9=2)r5c9 - (2=9)r5c5 - (2#9=1)r6c4 => -1 r5c6, r6c3; stte

What criterion determines your choice of the 15r5c1 pair to write such a complex string?

Sincerely
Robert

[pjb]

Hi Robert

None really. I determine which digit eliminations yield an stte finish, then generate chains systematically looking for one that gives the desired elimination. In puzzles far too hard for hand solving such as this, I see this as an reasonable approach.

Phil

[Mauriès Robert]

Hi Robert

None really. I determine which digit eliminations yield an stte finish, then generate chains systematically looking for one that gives the desired elimination. In puzzles far too hard for hand solving such as this, I see this as an reasonable approach.

Phil

Thank you, Phil.
Robert