Thanks for the link to the solver. However I am not familiar with the file type, I imagine I will have some looking around to do before I figure out how to run it.
coloin wrote:you may find this link interesting
diagonal-patterns-in-the-patterns-game-t30208.html
in it i could only generate 18 different patterns with one empty box.....
C
Very interesting work. However I am not particularly surprised by the result, for the empty boxes, and I can explain why the number is as small as it is.
It is possible to break down a pattern with 8 mini diagonals and an empty box into 3 sets of overlapping boxes containing mini-diagonals. When box 1 is empty, these sets would be boxes, {2,3,5,6}, {5,6,8,9}, and {4,5,7,8}.
If you look at 2x2 set of boxes containing mini diagonals there are only three fundamentally different ways to fill in the givens.
They are as follows:
Type 1: Three Box.
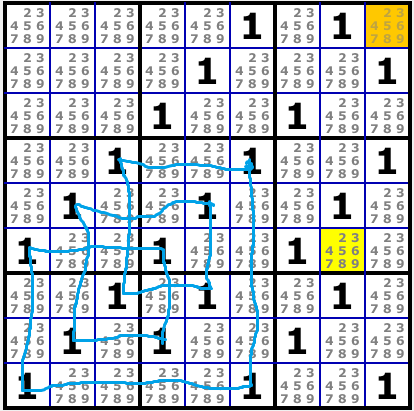
- Type 3
- aaa3.png (32.95 KiB) Viewed 1172 times
Type 2: Box + 8 Loop
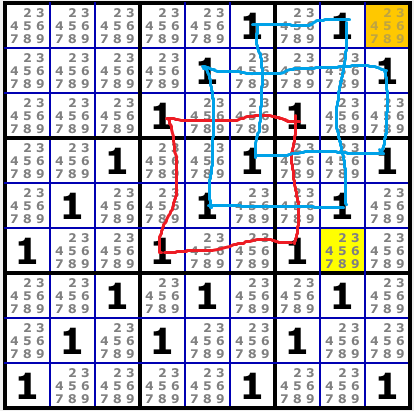
- Type 2
- aaa2.png (31.77 KiB) Viewed 1172 times
Type 3: 12 Loop
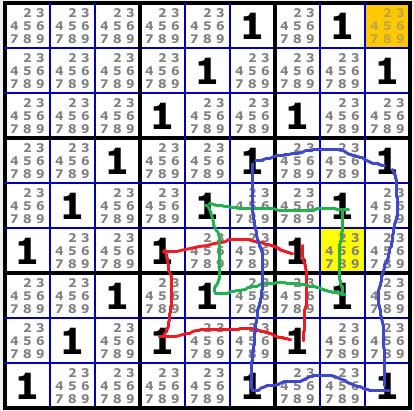
- Type 1
- aaa1.png (33.09 KiB) Viewed 1172 times
There are thus 27 possible combinations. However because {2,3,5,6} swaps with {4,5,7,8} under transpose, 9 of these are equivalent to others, which leaves 18 fundamentally different patterns.
Also since the contents of this thread are straying away from methods of solving the puzzle it might be worthwhile to move this to another subforum.

