The New Sudoku Players' Forum

[pavellek]

Hello,
I've started to solve Sudoku a few weeks ago and this is really a great fun for me. but at this one I have stucked.
I would be very thankful for every help.
This is the puzzle:
I have gone so far till now:
*---------*
|---|715|-28|
|--2|834|---|
|-8-|926|---|
|---+---+---|
|8--|463|215|
|126|597|834|
|354|182|976|
|---+---+---|
|---|27-|-8-|
|--8|34-|7-2|
|2--|658|---|
*------------*

Can any one show me what the next step shall be and why?
I'm not waiting for the complete solution, just for a technique which could help me get through the next step.
One more time with the pencilmarks:

[469][3469][39]715[346]28
[5679][1679]2834[356][569][179]
[457]8[1357]926[1345][45][137]
8[79][79]463215
126597834
354182976
[4569][13469][1359]27[19][13456]8[139]
[569][169]834[19]7[569]2
2[13479][1379]658[134][49][139]

Thank for every hint
Pavellek

[tso]

Code: Select all

 . . . | 7 1 5 | . 2 8
 . . 2 | 8 3 4 | . . .
 . 8 . | 9 2 6 | . . .
-------+-------+------
 8 . . | 4 6 3 | 2 1 5
 1 2 6 | 5 9 7 | 8 3 4
 3 5 4 | 1 8 2 | 9 7 6
-------+-------+------
 . . . | 2 7 . | . 8 .
 . . 8 | 3 4 . | 7 . 2
 2 . . | 6 5 8 | . . .

1) There are only two cells in box three that contain the candidate 9 (r2c89), they are both in row 2, which excludes the cadidate 9 from the rest of row 2.

2) There are only two cells in column 1 that can have the candidate 7 (r23c1), they are both in box 1, which excludes the candidate 7 from the rest of box 1.

3) There are exactly four cells in box 9 (r7c9, r9c789) that contain only the candidates 1, 3, 4 or 9, which is a NAKED QUAD [134][49][139][139], which eliminates these four candidates from the rest of box 9.

4) Now there are only two cells in box 9 that have the candidate 4 (r9c78), both of which are in row 9, which excludes the cadidate 4 from the rest of row 9.

Code: Select all

{469}   {3469}  {39}    {7}     {1}     {5}     {346}   {2}     {8}     
{567}   {16}    {2}     {8}     {3}     {4}     {156}   {569}   {179}   
{457}   {8}     {135}   {9}     {2}     {6}     {1345}  {45}    {137}   
{8}     {79}    {79}    {4}     {6}     {3}     {2}     {1}     {5}     
{1}     {2}     {6}     {5}     {9}     {7}     {8}     {3}     {4}     
{3}     {5}     {4}     {1}     {8}     {2}     {9}     {7}     {6}     
{4569}  {13469} {1359}  {2}     {7}     {19}    {56}    {8}     {139}   
{569}   {169}   {8}     {3}     {4}     {19}    {7}     {56}    {2}     
{2}     {1379}  {1379}  {6}     {5}     {8}     {134}   {49}    {139} 

End of easy part. At this point, both the bivalue and bilocation graphs are sparse and useless. Someone with more time and/or who is more clever must give the next step.

[Sue De Coq]

The key is the following chain in the 5s:

r3c8=5 => r3c3<>5 => r7c3=5 => r7c7<>5 => r8c8=5

It follows that r3c8 can't contain a 5 (otherwise there would be two 5s in Column 8), so we're left with the 4 as the only candidate for that cell. The remainder of the puzzle follows easily.

[Ocean]

Here is a possible continuation for the next step:
Filter on 5-candidates.
Note (color) the two conjugate pairs.
[Tried to put a picture here, but... anyway, there's only one way to do it]
Now, simple logic tells that there cannot be a 5 in r3c8.
Therfore, set r3c8=4.

[Ocean]

This example is an interesting illustration of a general phenomena:

Conjecture: If there are two separate conjugate chains A-B and C-D (for a candidate x), and these are linked by having B and C in a common unit, Then x can be excluded from all cells P that are linked to both A and D.

Proof by contradicion: (P=x & P=>notA & P=>notD) => B & C => B and C cannot share a unit.

Hope somebody arrest me if I'm wrong here...

[angusj]

Conjecture: If there are two separate conjugate chains A-B and C-D (for a candidate x), and these are linked by having B and C in a common unit, Then x can be excluded from all cells P that are linked to both A and D.

I think that's pretty much the premise on which x-wing, swordfish, jellyfish etc are based.

[Ocean]

Conjecture: If there are two separate conjugate chains A-B and C-D (for a candidate x), and these are linked by having B and C in a common unit, Then x can be excluded from all cells P that are linked to both A and D.

I think that's pretty much the premise on which x-wing, swordfish, jellyfish etc are based.

Yea.. ok maybe your're right, but...

1. I must admit I cannot find a single example from x-wing or swordfish where this principle apply.
2. I cannot see any x-wing-like or swordfish-like pattern in this particular example.

So, still wondering where the connection might be...

(think I probably expressed the conjecture unprecisely... )

[angusj]

Yea.. ok maybe your're right, but...

No, I wasn't.

I'd reverted to an old and restricted definition of x-wing, swordfish etc where your conjecture could equally apply. However, the newer more general definitions of x-wing, swordfish, jellyfish etc is based on an entirely different conjecture.

Anyhow, just to show your conjecture could apply to x-wing (and to the restricted definitions of swordfish etc) look at this example:

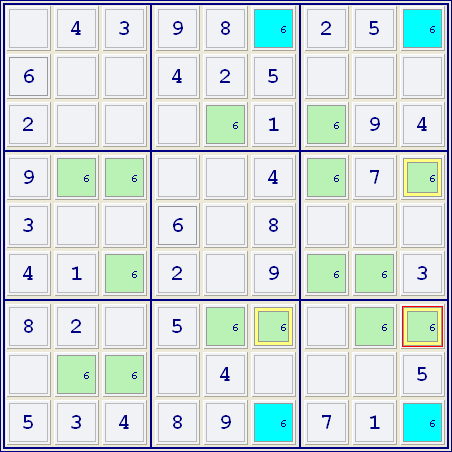
Let A&B be r1c6 & r1c9
Let C&D be r9c9 & r9c6
B&C have a common group (col9), as do A&D (col6). Hence 'other' cells sharing A&D's group can be excluded based on your conjecture. (In this example: r7c6 =6 => r1c6<>6 & r9c6<>6 => r1c9=6 & r9c9=6 is a contradiction.) Likewise, using the same conjecture, 'other' cells sharing B&C's group can be excluded.

[tso]

r3c8=5 => r3c3<>5 => r7c3=5 => r7c7<>5 => r8c8=5

How did you find this?

[Sue De Coq]

I found the chain with a computer-based solver rather than by hand. I've extended my old X-Wings/Swordfish code to seek chains of arbitrary length - first in single values, then in many values. I haven't even downloaded the paper by Eppstein - I use my own algorithms, which I'm yet to document (due to laziness, not secrecy). I prefer not to use terms such as Swordfish anymore, as any reference to the term on the forum is invariably followed by a request for an explanation. (I believe the pattern here is a 'Turbot Fish'). Instead, I simply list the chains I find with their accompanying reasoning in as near as possible to natural English.

The solver is hosted at http://act365.com/sudoku. This site contains a link to the (open) source, which, as things stand, is the best description I have of my chain-seeking code. A new release will be out soon.

[Ocean]

Anyhow, just to show your conjecture could apply to x-wing (and to the restricted definitions of swordfish etc) look at this example:
...

Thank you for the illustrative example!!

As far as I can see, the conjecture applies in fact to all x-wings!! and to some but not all swordfishes. (You were right from start, it was just that I could not figure it out, but I see the connection much clearer now...)

I didn't realize how important this connection to x-wings and swordfish is, giving insight into hidden logic. And WOW ... I still cannot believe what I see (and you should not until you have verified it for yourself):

Look at this candidate-grid:

Code: Select all

 *-----------*
 |..1|...|..1|
 |..1|111|...|
 |1.1|..1|1.1|
 |---+---+---|
 !1.1|..1|1.1|
 |1.1|...|111|
 |111|111|1.1|
 |---+---+---|
 |...|.11|..1|
 |..1|..1|...|
 |1..|...|1..|
 *-----------*

Which almost directly can be reduced to:

Code: Select all

 *-----------*
 |...|...|..1|
 |...|1..|...|
 |1..|...|...|
 |---+---+---|
 !...|..1|...|
 |...|...|.1.|
 |.1.|...|...|
 |---+---+---|
 |...|.1.|...|
 |..1|...|...|
 |...|...|1..|
 *-----------*

Believe it or not!!!

The process is simply based on the 'x-wing-lookalike' pattern:

Code: Select all

 *-----------*
 |..X|...|..X|
 |...|...|...|
 |...|...|...|
 |---+---+---|
 !...|...|...|
 |...|...|...|
 |...|...|...|
 |---+---+---|
 |...|...|..X|
 |..X|...|...|
 |X..|...|X..|
 *-----------*

OK, maybe most of you knew all this already, but I did not until now. Don't know how useful it is, but anyway there are more pattern to look for than I was aware of.

Thanks again to Angusj for inspiration!

[angusj]

The process is simply based on the 'x-wing-lookalike' pattern

Yes, that is certainly valid.

[Jeff]

The process is simply based on the 'x-wing-lookalike' pattern:

Code: Select all

 *-----------*
 |..X|...|..X|
 |...|...|...|
 |...|...|...|
 |---+---+---|
 !...|...|...|
 |...|...|...|
 |...|...|...|
 |---+---+---|
 |...|...|..X|
 |..X|...|...|
 |X..|...|X..|
 *-----------*   


Is the above pattern correct?

Conjecture: If there are two separate conjugate chains A-B and C-D (for a candidate x), and these are linked by having B and C in a common unit, Then x can be excluded from all cells P that are linked to both A and D.

Excellent observation again. You may like to know that what you have described is a case of turbot fish. Refer here

[angusj]

Is the above pattern correct?

Yes, it is.

However, I doubt it's a pattern that appears often and think it would require a fair bit of patience to spot. (I certainly wont be rushing out to add it to my solver program. )

[Jeff]

The process is simply based on the 'x-wing-lookalike' pattern:

Code: Select all

 *-----------*
 |..X|...|..X|
 |...|...|...|
 |...|...|...|
 |---+---+---|
 !...|...|...|
 |...|...|...|
 |...|...|...|
 |---+---+---|
 |...|...|..X|
 |..X|...|...|
 |X..|...|X..|
 *-----------*   


Ocean, could you please explain how this pattern is to be applied and how it is related to the conjecture.