The New Sudoku Players' Forum

[Jasper32]

This is a puzzle I picked off a web site for Sudoku. Below is the original puzzle and below that is how far I was able to get before I got stuck. The puzzle seems difficult to me and I hope you can help me out. I have spent about two hours working on the puzzle after getting stymied.

Code: Select all

 *-----------*
 |..9|.2.|7..|
 |...|.6.|...|
 |.36|5.7|48.|
 |---+---+---|
 |.12|...|85.|
 |5..|...|..6|
 |.93|...|21.|
 |---+---+---|
 |.67|1.9|52.|
 |...|.5.|...|
 |..5|.8.|3..|
 *-----------*

 


Code: Select all

 
 
 *--------------------------------------------------------------------*
 | 18     58     9      | 34     2      134    | 7      6      35     |
 | 27     257    4      | 39     6      8      | 1      39     25     |
 | 12     3      6      | 5      19     7      | 4      8      29     |
 |----------------------+----------------------+----------------------|
 | 47     1      2      | 469    379    346    | 8      5      347    |
 | 5      47     8      | 234    137    1234   | 9      347    6      |
 | 6      9      3      | 8      47     5      | 2      1      47     |
 |----------------------+----------------------+----------------------|
 | 348    6      7      | 1      34     9      | 5      2      48     |
 | 23489  248    1      | 2347   5      234    | 6      479    4789   |
 | 249    24     5      | 2467   8      246    | 3      479    1      |
 *--------------------------------------------------------------------*




[tarek]

I can't see an elegant single step to overcome this situation... multiple ALSs from me.

Hopefully somebody else might provide a better alternative

tarek

[EDIT: Possibly 2 steps to eliminate 9 in r3c5 .... Headache

Code: Select all

Eliminating 3 from r5c5(ALS-XY A=47 in r6c9 B=347 in r67c5 C=34 in r5c8 x=7 y=4 z=3)
Eliminating 1 from r3c5(ALS-XY A=47 in r4c1 B=127 in r23c1 C=147 in r5c25 x=7 y=4 z=1)

Will re-check & verify later ...Headache ]

[Luke]

On a wing and a prayer, here's simple mostly winged path:

Code: Select all

 *--------------------------------------------------------------------*
 | 18     58     9      | 34     2      134    | 7      6      35     |
 | 27     257    4      | 39     6      8      | 1      39     25     |
 | 12     3      6      | 5      19     7      | 4      8      29     |
 |----------------------+----------------------+----------------------|
 | 47     1      2      | 469    379    346    | 8      5      347    |
 | 5      47     8      | 234    137    1234   | 9      347    6      |
 | 6      9      3      | 8      47     5      | 2      1      47     |
 |----------------------+----------------------+----------------------|
 |*348    6      7      | 1      34     9      | 5      2     *48     |
 |*23489  248    1      | 2347   5      234    | 6      479   *4789   |
 | 249    24     5      | 2467   8      246    | 3      479    1      |
 *--------------------------------------------------------------------*

1. Hybrid Wing , strong links on 3, 8, and 9, =>r7c9<>4. (or: 4r7c9-9r8c9-3r8c1-8r7c1-4r7c9)
Edit: Apologies, this only works if there's not a 9 in r8c8 .
2. W-wing on (47) r4c1 + r6c5, strong link on 4 r7 => r4c5<>7.
3. W-wing on (47) r5c2 + r6c9, strong link on 7 r4 => r5c8<>4.
4. XY chain, starts r4c5 ends r5c8 => r4c9, r5c456<>3.

[aran]

Code: Select all

 *--------------------------------------------------------------------*
 | 18     58     9      | 34     2      134    | 7      6      35     |
 | 27     257    4      | 39     6      8      | 1      39     25     |
 | 12     3      6      | 5      19     7      | 4      8      29     |
 |----------------------+----------------------+----------------------|
 | 47     1      2      | 469    379    346    | 8      5      347    |
 | 5      47     8      | 234    137    1234   | 9      347    6      |
 | 6      9      3      | 8      47     5      | 2      1      47     |
 |----------------------+----------------------+----------------------|
 |*348    6      7      | 1      34     9      | 5      2     *48     |
 |*23489  248    1      | 2347   5      234    | 6      479   *4789   |
 | 249    24     5      | 2467   8      246    | 3      479    1      |
 *--------------------------------------------------------------------*

Plan B
347r4c159=9r4c5-(9=1)r3c5-(1=2)r3c1-(2=7)r2c1-(7=4)r4c1 : =><4>r4c46
347r4c159=9r4c5-9r3c5=9r3c9-(9=3)r2c8-3r5c8=3r4c9 : =><3>r4c6
singles to end.

[DonM]

There's all sorts of things you can do with this puzzle, but since there's been a lot of talk about Death Blossom, to add to the drama ( ) I'm willing to prostitute myself and call the following a DB (even though IMO, it's better seen as a 3-Set ALS Chain aka ALS xy-wing rule). What makes it somewhat more interesting is that it's mediated thru 2 conjugate links:



As an ALS Chain (as I've diagrammed it):
Green Set -> restricted common 1 -> Blue Set -> restricted common 9 -> conjugates 9 (r2c48) -> Brown Set

The Brown Set sees the 7 in r5c8 directly, the Green Set sees the 7 in r5c8 thru the conjugates 7 (r25c2). Therefore r5c8<>7

However, seen as a Death Blossom: the Blue Stem Cell sees the Green Set thru digit 1 and the Brown Set thru digit 9 via the conjugate 9s. Therefore since the Brown Set directly sees the 7 in r5c8 and the Green Set sees it thru the conjugate 7s, r5c8<>7

I continue to promote ALS Chains for those not quite up on nice loops/AICs because while they still involve pure Pattern A solving, they give some of the power of chains (Pattern B solving as I call it ie. this pattern could be expressed as a chain). If one is still having trouble following this, try alternately assigning the values 2 & 7 in r2c2 and following the effect (ie. follow the arrows) and see how in either case, r5c8<>7. My explaining of the basics is for those who will benefit from it, understanding that others already know this stuff.

[ronk]

There's all sorts of things you can do with this puzzle, but since there's been a lot of talk about Death Blossom, to add to the drama ( ) I'm willing to prostitute myself and call the following a DB (even though IMO, it's better seen as a 3-Set ALS Chain aka ALS xy-wing rule). What makes it somewhat more interesting is that it's mediated thru 2 conjugate links:

ALS xz rule and ALS xy wing rule are techniques based on sets, meaning that all native strong inferences are cell sets. Hence, strictly speaking, there are no conjugate links in an ALS xy wing.

Very nice chain using ALSs though.

[Luke]

1. Hybrid Wing , strong links on 3, 8, and 9, =>r7c9<>4. (or: 4r7c9-9r8c9-3r8c1-8r7c1-4r7c9)

Sorry, this move is invalid. Had marked a strong link on (9) in c9 and got it confused w/r8 . Thanks to ronk for the heads-up.

[DonM]

There's all sorts of things you can do with this puzzle, but since there's been a lot of talk about Death Blossom, to add to the drama ( ) I'm willing to prostitute myself and call the following a DB (even though IMO, it's better seen as a 3-Set ALS Chain aka ALS xy-wing rule). What makes it somewhat more interesting is that it's mediated thru 2 conjugate links:

ALS xz rule and ALS xy wing rule are techniques based on sets, meaning that all native strong inferences are cell sets. Hence, strictly speaking, there are no conjugate links in an ALS xy wing.

Very nice chain using ALSs though.

Appreciate the complement. On the matter of conjugate link terminology: As with some similar discussions, I think we defer because of cross-purposes. I am not a purist. On the contrary, I'm more interested in whatever helps me to be a better solver plus helping people solve manually and so I prefer the simplest & most basic terminology that gets the point across. The concept of conjugate pairs and conjugate links is pretty simple even to the newbie and that concept will immediately be recognized by anyone who now understands a basic strong link as I use it above. On the other hand, the possible need to base the terminology on the concept of sets while perhaps strictly true (and I'm not totally convinced even there, but will concede the possibility for the moment), would IMO only unnecessarily confuse someone trying to learn this stuff.

[ronk]

On the matter of conjugate link terminology: As with some similar discussions, I think we defer because of cross-purposes. I am not a purist. On the contrary, I'm more interested in whatever helps me to be a better solver plus helping people solve manually and so I prefer the simplest & most basic terminology that gets the point across.

"Basic" terminology, whatever that means, does not justify being careless with terminology, especially by someone who purports to be an expert.

[DonM]

On the matter of conjugate link terminology: As with some similar discussions, I think we defer because of cross-purposes. I am not a purist. On the contrary, I'm more interested in whatever helps me to be a better solver plus helping people solve manually and so I prefer the simplest & most basic terminology that gets the point across.

"Basic" terminology, whatever that means, does not justify being careless with terminology, especially by someone who purports to be an expert.

The question then becomes: Who is the one purporting to be the expert: the one who simply puts up some examples with simple explanations or the one constantly questioning them?

[aran]

Don, you purporting expert, when the terminology becomes a strait-jacket, I too am in favour of moving on.
But back to your original post above.
A word on the hidden set view of things : they point straight at their targets, and the targets are at close range. Which is why I regard this as a simple approach.
Simpler and arguably better than "simple" chains by which I mean those which start on a single candidate (xr1c1=...)
For a reason which could even appeal to you : they are closer to "Pattern A" solving : why ? because the latter shall we say hope to catch a candidate in a pincer movement, and any candidate will do, whereas hidden set chains know exactly what targets they have in mind.
So when a "Pattern B tending towards A" is staring you in the face, is it preferable to construct a Pattern A ? Let that be a rhetorical question.
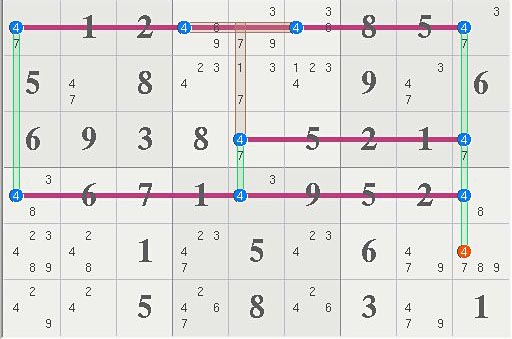
Take now your example :

Look at 479r89c8 : 7r5c8 looks like a natural target (which doesn't mean that it will turn out to be one).
The logic :
either r89c9 is the hidden pair 47, or there is a 9 in r89c9.
If it is the pair, the case is closed : <7>r5c8
If it isn't, then a little chain with 9 soon places 7 in r5c2.
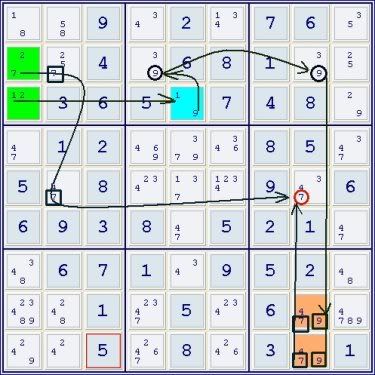
For variety as compared to your steps :
9r89c8-(9=3)r2c8-(3=5)r1c9-(5=8)r1c2-(8=24)r89c2-(4=7)r5c2 : <7>r5c8
That reasoning is then combined into one chain :
47r89c8=9r89c8-(9=3)r2c8-(3=5)r1c9-(5=8)r1c2-(8=24)r89c2-(4=7)r5c2 : <7>r5c8.

[ronk]

"Basic" terminology, whatever that means, does not justify being careless with terminology, especially by someone who purports to be an expert.

The question then becomes: Who is the one purporting to be the expert: the one who simply puts up some examples with simple explanations or the one constantly questioning them?

We were discussing your use of the ALS xy wing term. If there's a relevant point in your reply above, I don't see it.

Relevantly, observe that by analogy to your use of the ALS xy wing term, the below is an xy-wing.

Code: Select all

                           ___ conjugate link on 'y'     
                          V

 .  .  .  | .  .  .  | .  /  .
 . *xy .  | .  .  .  | .  y  .
 .  .  .  | .  .  .  | .  /  .
----------+----------+---------- 
 /  x  /  | /  x  /  | /  /  /  <-- conjugate link on 'x'
 .  .  .  | .  .  .  | .  /  .
 .  .  .  | .  .  .  | .  /  .
----------+----------+---------- 
 .  . *yz |-z -z -z  | .  y  .
 .  .  .  | .  .  .  | .  /  .
-z -z -z  | . *xz .  | .  /  .

 xy-wing

[aran]

Relevantly, observe that by analogy to your use of the ALS xy wing term, the below is an xy-wing.

Relevant grammar : by analogy with/analogous to

[Allan Barker]

Mutant rank 1 to rank 0 promotion fish, r8c9<>4

I have always wanted to ask to how describe this. In terms of cover sets, the triplet 4r6c5 lowers the rank on the right to 0 to eliminate 4r8c9. I'm sure there is a better way.

Code: Select all

+---------------+--------------------+---------------+
| 18     58   9 | 34     2     134   | 7  6    35    |
| 27     257  4 | 39     6     8     | 1  39   25    |
| 12     3    6 | 5      19    7     | 4  8    29    |
+---------------+--------------------+---------------+
| 7(4)   1    2 | 69(4)  379   36(4) | 8  5    37(4) |
| 5      47   8 | 234    137   1234  | 9  347  6     |
| 6      9    3 | 8      7(4)  5     | 2  1    7(4)  |
+---------------+--------------------+---------------+
| 38(4)  6    7 | 1      3(4)  9     | 5  2    8(4)  |

| 23489  248  1 | 2347   5     234   | 6  479  789-4 |
| 249    24   5 | 2467   8     246   | 3  479  1     |
+---------------+--------------------+---------------+

[ronk]

Mutant rank 1 to rank 0 promotion fish, r8c9<>4

I have always wanted to ask to how describe this. In terms of cover sets, the triplet 4r6c5 lowers the rank on the right to 0 to eliminate 4r8c9. I'm sure there is a better way.

I would start with this.

Code: Select all

 .  .  . |  4  .  4 |  .  .  .
 .  .  . |  .  .  . |  .  .  .
 .  .  . |  .  .  . |  .  .  .
---------+----------+----------
*4  .  . | *4  . *4 |  .  . *4
 .  4  . |  4  .  4 |  .  4  .
 .  .  . |  . *4  . |  .  . *4
---------+----------+----------
*4  .  . |  . #4  . |  .  . *4
 4  4  . |  4  .  4 |  .  4 -4
 4  4  . |  4  .  4 |  .  4  .

finned franken swordfish r467\c19b5 plus fin r7c5

r8c9 -4- r6c9 =4= r6c5 -4- fin:r7c5 =4= swordfish:r467\c19b5 -4- r8c9 ==> r8c9<>4

Either the unfinned (franken) swordfish is true or the fin cell is true.
If the unfinned swordfish is true: r467\c19b5 -4- r8c9
If the fin is true: r7c5 -4- r6c5 =4= r6c9 -4- r8c9

The r7c5 -4- r6c5 segment corresponds to 4c5 being a linkset member. Alternatively, the fish could be considered to be finned swordfish r467\c159 plus fin r4c46.

Interestingly, neither POV puts the fin at the linkset triple r6c5.