The New Sudoku Players' Forum

[Nico]

Would have it been possible to continue without making a guess?

Bonjour Nico. You can solve it with a fairly simple forcing chain:



Regardless of the candidate assigned in cell r6c7, the cell r5c2 must be 4.

Hello again angusj,

I "studied" this chain, but there is something that I don't understand.

So, let's start at cell r6c7 and assume it is a 2.
So r6c8 is 5 => r6c1 is 7 => r4c3 is 2 => r4c2 is 4 => r5c2 is 5 !!!! (not 4!).

So whats' wrong?

Thank you.

Nico'

[tso]

Three people go into a hotel. The desk clerk says the rooms are $30, so each person pays $10 and goes to the room. Later, the clerk realizes that the room is only $25 and sends a bellhop to thre room with the $5 difference. The bellhop couldn’t figure out how to split the $5 three ways, so instead, gives each person a dollar and keeps $2 as a “tip”. Each person paid $9 for the room -- a total of $27 -- the bellhop kept $2 -- that makes $29. Where’s the extra dollar?

Of course, there is no extra dollar. They paid $27, two of which is in the bellhop's pocket. The other three are back in their wallets. The "extra dollar" is a phantom.

This is what you've done by including this other another chain. The point of forcing chains is this: If ALL candidates of a single cell lead can start an implication chain that lead to the same conclusion, since ONE of the candidates MUST be true, then the CONCLUSION must also be true. The fact that you can "assume r6c7 is 2" and find that it implies something different is the two dollars in the bellhop's pocket. In retrospect, the reason you can do this is because your assumption was false! Forcing chains does NOT make any assumtions.

The chain could be thought of as a proof by contradiction, since if you assume there is a 5 in r5c2, the two sides of the chain lead to contradictory resultes in r6c7. This is valid, but some find this less satisfying since you are making an assumption -- a guess.

To be fair, the statement "Regardless of the candidate assigned in cell r6c7, the cell r5c2 must be 4." isn't quite accurate unless you restrict yourself to the highlighted cells. The point is that an implication chain can be made from each of the two candidates in r6c7 that lead to the same results in r5c2. The fact that other implication chains exist that don't agree does not matter. This will often be the case.


Another way to look at the same situtation is to consider the forcing chain as a closed loop connected by labled edges:



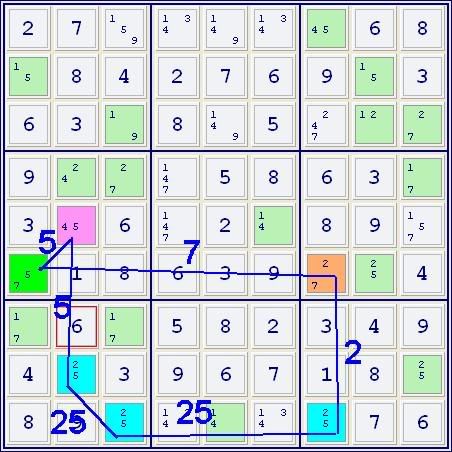
This forms a loop with a single repetion:

[5]-[5]-[2(5)]-[(2)5]-[2]-[7]

The links in () are not used, leaving:

[5]-[5]-[2]-[5]-[2]-[7]

The 5s repeat -- eliminating the 5 in the cell they have in common.

[PaulIQ164]

Aah, how I hate that puzzle.

[Nico]

This is what you've done by including this other another chain. The point of forcing chains is this: If ALL candidates of a single cell lead can start an implication chain that lead to the same conclusion, since ONE of the candidates MUST be true, then the CONCLUSION must also be true. The fact that you can "assume r6c7 is 2" and find that it implies something different is the two dollars in the bellhop's pocket. In retrospect, the reason you can do this is because your assumption was false! Forcing chains does NOT make any assumtions.

Hello tso,

Thank you for your great explanation.

I understand well that if I find another chain that leads to a contradiction with the other ones, then I can conclude that my assomption was false. (I hope you understand me, again, sorry for my bad English ). And I understand that it does not mean that the conclusion with the other chains was false.

But actually, i didn't know what chains angusj was talking about... There were so many colors in the picture that I didn't figure out what chains he was talking about... So, if I understand, chains begin in the orange cell, then one continues in the blue cells (the one that begins with a "2" in the orange cell), the other continues in the light green cell (the one that begins with a "7" in the orange cell), and both chains end in the purple cell.

So, light green chain is : r6c7 = 7 => r6c1 = 5 => r5c2 = 4
And blue chain is : r6c7 = 2 => r9c7 = 5 => r9c3 = 2 => r8c2 = 5 => r5c2 = 4
Wichever value is r6c7, r5c2 is 4. Ok!

By the way, what do mean the dark green cells?

But I didn't figured out your last theory, about the "closed loop connected by labled edges". I'm going to "sleep on it" (don't know if you say this in English), and tomorrow, maybe I will get that quickly.

Thanks.

Nico'

[Karyobin]

What a nice Frenchman.

[PaulIQ164]

And yes, we English indeed do sleep on things.


Some moreso than others.

[r.e.s.]

The online solver at http://act365.com/sudoku/ solves this puzzle using two short forcing chains (of lengths 4 and 5).

Could you list the 2 chains for us? Thank you.

Omitting all the simple moves ...

Chain#1: (1,7)-5-(1,3)-5-(9,3)-5-(9,7) => (6,7)<>5.
Chain#2: (6,7)-2-(6,8)-5-(5,9)-5-(8,9)-2-(9,7) => (6,7)<>2 and (9,7)<>2.

PS: To make it easier for people to try out that solver (which I believe is the work of "rubylips") so they can read the step-by-step explanations for themselves, here's the puzzle in a format the solver can read:

Code: Select all

 2 7 . | . . . | . 6 8
 . . 4 | 2 . . | 9 . .
 6 . . | 8 . 5 | . . .
-------+-------+------
 9 . . | . 5 . | 6 3 .
 . . . | . 2 . | . . .
 . 1 8 | . 3 . | . . 4
-------+-------+------
 . . . | 5 . 2 | . . 9
 . . 3 | . . 7 | 1 . .
 8 9 . | . . . | . 7 6

Click the solver's Copy button, paste the above into the window that opens, then click the solver's Paste button.

[angusj]

What a nice Frenchman.

The only sort I know (except for those on the rugby field ).

[9X9]

Que vous passiez une bonne nuit sans cauchmar sudokien Nico.

[QBasicMac]

I don't get what is being discussed here.

Why does the "Solution so far" not have r3c2=3, as obvious from the pencilmarks?

Anyway, if I start with no pencilmarks and complete the easy stuff that involves no chains, etc., I get

27- --- -68
-84 276 9-3
63- 8-5 ---
9-- -58 63-
3-6 -2- 89-
-18 639 --4
-6- 582 349
4-3 967 18-
89- --- -76

Continuing with easy stuff:
r3c9: {123}->{27} because of the 1's in box 6
r9c3: {125}->{25} because of the 1's in box 8
r4c9: {127}->{17} because of the 2's in box 4

But now stuck.

Well, guessing r2c8=1 leads to the quick solution of box 3 as
568
913
427

However, box 6 will then have a contradiction on candidates 1 and 5.

So it must be that r2c8=5

Mac

[Doyle]

I don't get what is being discussed here.

Obviously. Nico asked for a solution without guessing.

[tso]

But actually, i didn't know what chains angusj was talking about... There were so many colors in the picture that I didn't figure out what chains he was talking about...

You got it right.

By the way, what do mean the dark green cells?

No idea -- I'm colorblind! But don't give too much thought as to why they were colored the way they were -- he was just highlighting them for you. All the cells that had exactly 2-candidates were tinted, then all those on one chain were tinted another color, than the one cell on the other path was tinted yet another color (dark green I guess).

But I didn't figured out your last theory, about the "closed loop connected by labled edges". I'm going to "sleep on it" (don't know if you say this in English), and tomorrow, maybe I will get that quickly.

It isn't my theory. The first I saw it was in the second half of David Eppstein's paper "Nonrepetitive Paths and Cycles in Graphs with Application to Sudoku" which you can find here. It's far simpler than the the method I had been using.

It has been illustrated several times on the forum, for example
http://forum.enjoysudoku.com/viewtopic.php?t=1788

[QBasicMac]

[quote="Doyle"]
Obviously. Nico asked for a solution without guessing.
[/quote]

Err, true. I call making a simple choice that is obviouosly going to lead to a dead end a guess, even though it was done merely to establish the other choice as unique and correct. So at the point of my guess, I presume the chain-technique would be applicable.

My confusion was why obvious choices already apparent in the original pencilmarks were not taken first.

But anyway, don't bother answering. The answer is probably obvious anyway.

Mac

[tso]

Looking at the first graphic in this thread posted by Angusj, I found a short forcing chain using only 5 cells, but one of the links is a naked pair:

r6c8=2 => r3c8=1
r6c8=5 => r56c9=[17][17] => r3c9=2 = r3c8=1
Therefore, r2c8=1

The rest is naked singles.

If you consider r56c9 as a unit, you can draw labeled edges and solve it by the repetitive loop method:

Code: Select all


       (2)
  [12]-----[27]
   |         | (7)
   |       [17]
   |        |||
(2)|       [157]   
   |        /   
   |       /   
   |      /(5) 
   |     /     
  [25]--/         
 


The edges are 2275. The 2's repeat so you can eliminate the candidate 2 from the cell they both are connected to.