How to call this pattern
13 posts
• Page 1 of 1
How to call this pattern
R1C7 or R4C7 must be 5.
a) R1C7=5 leads to a pair 68 at R1C23 ==> R2C3<>8
b) R4C7=5 leads to R4C4=4 and R4C3=8 ==> R2C3<>8
- urhegyi
- Posts: 763
- Joined: 13 April 2020
Re: How to call this pattern
Hi urhegyi
Your method of eliminating 8r2c3 is what I call the Track Technique (TDP). It allows you to solve almost any puzzle using pairs of candidates or groups of candidates (strong links).
It can be written like this:
P(5r1c7) : 5r1c7->3r1c5->8r2c5
P(5r4c7) : (5r4c7->4r4c4)->8r4c3
These two tracks being conjugated, from this we deduce -8r2c3, because 8r2c5 and 8r4c3 see 8r2c3.
While the patterns (Wing, Fish, ALS, etc...) only give partial results, TDP generally deals more deeply with the puzzle.
For example, this ALS-XZ allows to eliminate only the 8r2c3, whereas with your same tracks you can find more elimination at once, like this :
P(5r1c7) : 5r1c7->[(3r1c5->8r2c5) and (6r3c9->6r2c4->7r2c1)]
P(5r4c7) : (5r4c7->4r4c4)->(8r4c3 and 56r1c23)->4r2c3
From this we deduce -8r2c3, -4r2c14, -5r2c1
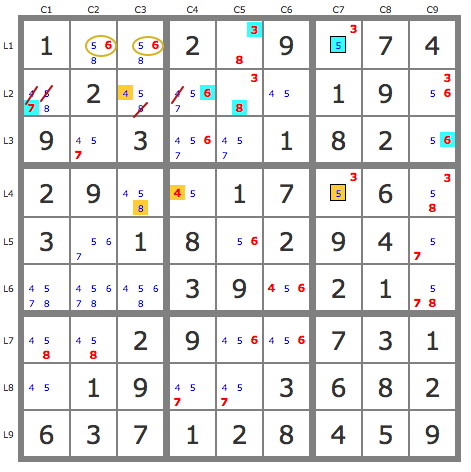
You can also represent these two tracks with AICs.
Cordialy
Robert
urhegyi wrote:R1C7 or R4C7 must be 5.
a) R1C7=5 leads to a pair 68 at R1C23 ==> R2C3<>8
b) R4C7=5 leads to R4C4=4 and R4C3=8 ==> R2C3<>8
Your method of eliminating 8r2c3 is what I call the Track Technique (TDP). It allows you to solve almost any puzzle using pairs of candidates or groups of candidates (strong links).
It can be written like this:
P(5r1c7) : 5r1c7->3r1c5->8r2c5
P(5r4c7) : (5r4c7->4r4c4)->8r4c3
These two tracks being conjugated, from this we deduce -8r2c3, because 8r2c5 and 8r4c3 see 8r2c3.
While the patterns (Wing, Fish, ALS, etc...) only give partial results, TDP generally deals more deeply with the puzzle.
For example, this ALS-XZ allows to eliminate only the 8r2c3, whereas with your same tracks you can find more elimination at once, like this :
P(5r1c7) : 5r1c7->[(3r1c5->8r2c5) and (6r3c9->6r2c4->7r2c1)]
P(5r4c7) : (5r4c7->4r4c4)->(8r4c3 and 56r1c23)->4r2c3
From this we deduce -8r2c3, -4r2c14, -5r2c1

You can also represent these two tracks with AICs.
Cordialy
Robert
Last edited by Mauriès Robert on Fri Nov 06, 2020 6:38 am, edited 1 time in total.
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: How to call this pattern
Hi urhegyi,
That logic is not in sync with the pattern in the image. The image depicts an ALS-XZ, just like yzfwsf said. What you wrote describes a different pattern that is actually simpler, thus better.
It's what I call ALS-Z, because it skips the X-candidate (i.e. the restricted common digit, RCD), which is not needed if the two subsets are directly strongly-linked. I don't know if anyone else has named that pattern, but I think it deserves its own name.
In my experience almost all ALS-Zs can also be written as ALS-XZs, but the reverse is not true. Almost (or perhaps) all (UVW)XY(Z)-Wings are ALS-Zs, but that reverse is not true either (e.g. this is not a wing pattern).
The difference as AICs:
As can be seen, the latter is simpler, shorter, and more elegant. I use ALS-Zs instead of ALS-XZs when possible.
urhegyi wrote:R1C7 or R4C7 must be 5.
a) R1C7=5 leads to a pair 68 at R1C23 ==> R2C3<>8
b) R4C7=5 leads to R4C4=4 and R4C3=8 ==> R2C3<>8
That logic is not in sync with the pattern in the image. The image depicts an ALS-XZ, just like yzfwsf said. What you wrote describes a different pattern that is actually simpler, thus better.
It's what I call ALS-Z, because it skips the X-candidate (i.e. the restricted common digit, RCD), which is not needed if the two subsets are directly strongly-linked. I don't know if anyone else has named that pattern, but I think it deserves its own name.
In my experience almost all ALS-Zs can also be written as ALS-XZs, but the reverse is not true. Almost (or perhaps) all (UVW)XY(Z)-Wings are ALS-Zs, but that reverse is not true either (e.g. this is not a wing pattern).
The difference as AICs:
- Code: Select all
ALS-XZ (X=3, Z=8): (856=3)r1c237 - (3=548)r4c743 => -8 r2c3
ALS-Z ( Z=8): (865)r1c237 = (548)r4c743 => -8 r2c3
As can be seen, the latter is simpler, shorter, and more elegant. I use ALS-Zs instead of ALS-XZs when possible.
-SpAce-: Show
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: How to call this pattern
Hi Robert,
Yes, but it doesn't make much sense in this scenario. Eliminating 8r2c3 is enough because it reveals the naked pair (45)r2c36 which eliminates all those extras and 5r2c49 as well. It's much simpler and more efficient than continuing those tracks.
Btw, once again your notation is hard to follow, because it doesn't show exactly what leads to 56r1c23. It would be much easier if you added the negative implications (i.e. left-linking candidates) at least for the non-obvious parts. (Avoiding typos in them would help too )
)
In this case it's easy to write simple AICs for all of those eliminations, but not all at once. In general, it's not safe to assume that all tracks and anti-tracks can be written as reasonable AICs. The former use all possible memories freely, but AICs are restricted to being linked to the adjacent nodes only. Thus any branching or memory-intensive logic gets quickly complicated with AICs, as they must use split-nodes and/or nested AICs to implement that.
In this case there's no reason for such complications, because eliminating 8r2c3 is the key. The simplest option is probably this:
Mauriès Robert wrote:For example, this ALS-XZ allows to eliminate only the 8r2c3, whereas with your same tracks you can find more elimination at once, like this :
P(5r1c7) : 5r1c7->[(3r1c5->8r2c5) and (6r3c9->6r2c4->7r2c1)]
P(5r4c7) : (5r4c7->4r4c4)->(8r4c3 and 56r1c3)->4r2c3
From this we deduce -8r2c3, -4r2c14, -5r2c1
Yes, but it doesn't make much sense in this scenario. Eliminating 8r2c3 is enough because it reveals the naked pair (45)r2c36 which eliminates all those extras and 5r2c49 as well. It's much simpler and more efficient than continuing those tracks.
Btw, once again your notation is hard to follow, because it doesn't show exactly what leads to 56r1c23. It would be much easier if you added the negative implications (i.e. left-linking candidates) at least for the non-obvious parts. (Avoiding typos in them would help too
You can also represent these two tracks with AICs.
In this case it's easy to write simple AICs for all of those eliminations, but not all at once. In general, it's not safe to assume that all tracks and anti-tracks can be written as reasonable AICs. The former use all possible memories freely, but AICs are restricted to being linked to the adjacent nodes only. Thus any branching or memory-intensive logic gets quickly complicated with AICs, as they must use split-nodes and/or nested AICs to implement that.
In this case there's no reason for such complications, because eliminating 8r2c3 is the key. The simplest option is probably this:
- M2-Wing: (8=3)r2c5 - r2c9 = (3-8)r4c9 = (8)r4c9 => -8 r2c3
- M2-Wing: (83)r2c59 = (38)r4c93 => -8 r2c3
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: How to call this pattern
Hi Space,
My goal here was only to show that one could work more deeply with two tracks. I have more convincing examples that show this obviously with an advantage to the tracks.
In terms of my ratings, I understand that it would be more readable to indicate negative implications, but this would not be consistent with my definitions in TDP. Let me explain.
Tracks and anti-tracks are defined as sets of candidates that are placed with the TB (Basics Techniques). Deleted candidates (negative implications) are not candidates belonging to tracks or anti-tracks. My A->B->C rating ... lists the candidates belonging to the track or antitrack, specifying the order in which they are placed. When I place A, it is as if the puzzle G becomes a puzzle G+A with one more unveiled , puzzle G+A to which I apply the TB.
When you receive a puzzle, first you simplify it with the TB without specifying the negative implications. How much harder would it be to do this when you add a candidate as an additional unveiler!
Of course you have to look at the puzzle to follow and make an effort to remember. But isn't sudoku an intellectual exercise using memory!
Cordialy
Robert
SpAce wrote:Yes, but it doesn't make much sense in this scenario. Eliminating 8r2c3 is enough because it reveals the naked pair (45)r2c36 which eliminates all those extras and 5r2c49 as well. It's much simpler and more efficient than continuing those tracks.
My goal here was only to show that one could work more deeply with two tracks. I have more convincing examples that show this obviously with an advantage to the tracks.
SpAce wrote:Btw, once again your notation is hard to follow, because it doesn't show exactly what leads to 56r1c23. It would be much easier if you added the negative implications (i.e. left-linking candidates) at least for the non-obvious parts. (Avoiding typos in them would help too)
In terms of my ratings, I understand that it would be more readable to indicate negative implications, but this would not be consistent with my definitions in TDP. Let me explain.
Tracks and anti-tracks are defined as sets of candidates that are placed with the TB (Basics Techniques). Deleted candidates (negative implications) are not candidates belonging to tracks or anti-tracks. My A->B->C rating ... lists the candidates belonging to the track or antitrack, specifying the order in which they are placed. When I place A, it is as if the puzzle G becomes a puzzle G+A with one more unveiled , puzzle G+A to which I apply the TB.
When you receive a puzzle, first you simplify it with the TB without specifying the negative implications. How much harder would it be to do this when you add a candidate as an additional unveiler!
Of course you have to look at the puzzle to follow and make an effort to remember. But isn't sudoku an intellectual exercise using memory!
Cordialy
Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: How to call this pattern
Mauriès Robert wrote:My goal here was only to show that one could work more deeply with two tracks. I have more convincing examples that show this obviously with an advantage to the tracks.
Of course you do. This just happened to be a poor example to showcase that. Besides, you chose an inefficient and complicated route to do it. Why not:
- P(5r1c7): {5r1c7, 68r1c23, 45r2c36}
P(5r4c7): {5r4c7, 4r4c4, 8r4c3, 45r2c36}
=> +45r2c36 (or: -8r2c3, -45r2c24, -5r2c9)
I understand that it would be more readable to indicate negative implications
Good!
but this would not be consistent with my definitions in TDP.
It would be if your definitions were consistent in the first place. Sets and sequences are not the same thing, and you should more clearly separate the two concepts.
Tracks and anti-tracks are defined as sets of candidates that are placed with the TB (Basics Techniques).
I think that definition is limited and doesn't correspond with how you express and use tracks. Tracks have characteristics of both sets and sequences, so it doesn't seem right to say they're just one or the other. In particular, they're definitely not just sets, because sets are unordered.
The end result of a track is indeed a set of candidates, but to obtain that you need a sequential process and a notation that depicts it. Even the name 'track' implies a specific route and thus an ordered sequence of candidates, which can't be expressed with a set. As sets, all of these tracks are exactly the same:
- P(5r4c7): {5r4c7, 4r4c4, 8r4c3, 45r2c36}
P(5r4c7): {45r2c36, 4r4c4, 5r4c7, 8r4c3}
P(5r4c7): {8r4c3, 5r4c7, 45r2c36, 4r4c4}
Deleted candidates (negative implications) are not candidates belonging to tracks or anti-tracks.
That's not completely true, because you do include (or at least write) the starting negative in your anti-tracks! (In fact, I think that's mostly unnecessary. The opposite starting value is typically trivial to see anyway, and anti-tracks would look cleaner without it. The negatives would be much more helpful in other cases where you refuse to write them.)
My A->B->C rating ... lists the candidates belonging to the track or antitrack, specifying the order in which they are placed.
Here you're talking about the order of those candidates, expressed with implications, so you're no longer talking about just sets at all. That's the part with sequential logic, and you could freely add negative implications into it without breaking your definitions. The actual set of candidates forming the track can be extracted from that logic just as well, just like they can be from the right-linking-candidates in Denis' notation. The negatives wouldn't break it any more than the left-linking candidates do.
I don't see anything conflicting with your definitions if the sequences of tracks are written like this:
- P(5r1c7): 5r1c7 -> -5r1c23 -> 68r1c23 -> -8r2c3 -> 45r2c36
P(5r4c7): 5r4c7 -> -5r4c4 -> 4r4c4 --> -45r4c3 -> 8r4c3 -> -8r2c3 -> 45r2c36
=> +45r2c36
(The '-->' means a memory is being used. I just came up with that to avoid nested brackets and such. Not standard.)
Of course you have to look at the puzzle to follow and make an effort to remember. But isn't sudoku an intellectual exercise using memory!
I'm sorry, but that is the poorest excuse for a bad notation I've seen!
With your notation there's no choice to skip that if I want to understand what's going on. That's not an intellectual exercise. It's just tedious, and also completely unnecessary because much better notations exist that avoid it. You can choose not to care, but please don't pretend that it's a good thing that your notation requires such extra work from the reader!
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: How to call this pattern
Hi Space,
I regret to contradict you, tracks and anti-tracks are sets of candidates. I refer you to their definitions here. Nowhere in these definitions is it written that they are ordered sets, the reason being precisely that a track (or an anti-track) can be constructed by following different sequences, but it is the same track. The tracks as you write them in this example are the same as the ones I write, the difference comes from the fact that you and I only wrote some of the track candidates in different sequences. Thus, I maintain that the sequence is not a character of the track.
On the other hand, in order to explain how the (partial) set of candidates of a track is constructed, it is useful to describe the sequence that was used. I still refer you to my original document on this forum here to see that I'm talking about a construction diagram which does not represent the track but explains how it was constructed.
Not at all, when I represent an anti-track, therefore in the form of a set {B1,B2,...} I do not include the generator of the anti-track. But in the diagram, obviously, I indicate which is the generator in the form (-A).
Yes we can do that. I will think about it.
Cordialy
Robert
Space wrote:I think that definition is limited and doesn't correspond with how you express and use tracks. Tracks have characteristics of both sets and sequences, so it doesn't seem right to say they're just one or the other. In particular, they're definitely not just sets, because sets are unordered.
I regret to contradict you, tracks and anti-tracks are sets of candidates. I refer you to their definitions here. Nowhere in these definitions is it written that they are ordered sets, the reason being precisely that a track (or an anti-track) can be constructed by following different sequences, but it is the same track. The tracks as you write them in this example are the same as the ones I write, the difference comes from the fact that you and I only wrote some of the track candidates in different sequences. Thus, I maintain that the sequence is not a character of the track.
On the other hand, in order to explain how the (partial) set of candidates of a track is constructed, it is useful to describe the sequence that was used. I still refer you to my original document on this forum here to see that I'm talking about a construction diagram which does not represent the track but explains how it was constructed.
Space wrote:That's not completely true, because you do include (or at least write) the starting negative in your anti-tracks!
Not at all, when I represent an anti-track, therefore in the form of a set {B1,B2,...} I do not include the generator of the anti-track. But in the diagram, obviously, I indicate which is the generator in the form (-A).
Space wrote:I don't see anything conflicting with your definitions if the sequences of tracks are written like this:
P(5r1c7): 5r1c7 -> -5r1c23 -> 68r1c23 -> -8r2c3 -> 45r2c36
P(5r4c7): 5r4c7 -> -5r4c4 -> 4r4c4 --> -45r4c3 -> 8r4c3 -> -8r2c3 -> 45r2c36
=> +45r2c36
The set of candidates forming the track can still be read easily just by following the positive implications (colored here for clarity).
Yes we can do that. I will think about it.
Cordialy
Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: How to call this pattern
Mauriès Robert wrote:SpAce wrote:I think that definition is limited and doesn't correspond with how you express and use tracks. Tracks have characteristics of both sets and sequences, so it doesn't seem right to say they're just one or the other. In particular, they're definitely not just sets, because sets are unordered.
I regret to contradict you, tracks and anti-tracks are sets of candidates. I refer you to their definitions here.
You're right about the definitions, but I don't think it contradicts what I said very much. The practical reality is much more blurred. These days you mostly present construction diagrams when you talk about tracks, so the source of confusion is obvious. If you present a sequence and call it a track or label it with P(x), isn't it natural to assume that tracks are sequences instead of (or in addition to) sets?
It might be partially my fault, because I remember complaining about the fact that your original tracks were presented as sets only. In fact, I'm not sure that your original texts (on this forum) even mentioned construction diagrams, but that can't be verified because you've deleted them.
Btw, your link didn't work because of a typo. It's corrected in the quote above.
SpAce wrote:That's not completely true, because you do include (or at least write) the starting negative in your anti-tracks!
Not at all, when I represent an anti-track, therefore in the form of a set {B1,B2,...} I do not include the generator of the anti-track. But in the diagram, obviously, I indicate which is the generator in the form (-A).
That's what I meant. I should have written 'anti-track sequences'. I didn't think you'd include the negative in the actual set. But, like I said, that distinction is less and less clear since you mostly present construction diagrams. Either way, I don't see the necessity of including the negative as a special case here because it's implied by the P'(x) label.
That said, since it is already being used in this one situation, it could just as well be used anywhere. Like I said, it wouldn't break your definitions, since the construction diagram is not a track. It should be able to include any information that helps reading the actual sequence of steps to arrive at the set of singles that form the track.
Yes we can do that. I will think about it.
Glad to hear that.
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: How to call this pattern
Hi Space,
Yes, I added to my original English text the diagrams in the form P: A->B->C... following your remarks on the only representation P={A, B, C,... } that I used at the beginning of my participation in this forum. It has not escaped you either that for the sequence (diagram) I use ":" and not "=" which distinguishes between sequence and set.
To end this discussion, because I think we have said everything about the essential, just a little word about the terms Track and Anti-Track.
When I first became interested in sudoku in 2007, I used this term because I was solving fairly easy puzzles with this method and the sequences reminded me of "tracks". A little later I used the term anti-track, maybe I should have said "counter-track".
Finally, in 2011, when I started publishing my concepts, I would have liked to use the terms network and counter-network instead of track and anti-track. But then I discovered the work of Frenchman Bernard Borrelly and his method "Coloriage virtuel" where he used these terms. So I kept track and anti-track. I find that network is the most appropriate term: TDP is a network method.
Cordialy
Robert
Yes, I added to my original English text the diagrams in the form P: A->B->C... following your remarks on the only representation P={A, B, C,... } that I used at the beginning of my participation in this forum. It has not escaped you either that for the sequence (diagram) I use ":" and not "=" which distinguishes between sequence and set.
To end this discussion, because I think we have said everything about the essential, just a little word about the terms Track and Anti-Track.
When I first became interested in sudoku in 2007, I used this term because I was solving fairly easy puzzles with this method and the sequences reminded me of "tracks". A little later I used the term anti-track, maybe I should have said "counter-track".
Finally, in 2011, when I started publishing my concepts, I would have liked to use the terms network and counter-network instead of track and anti-track. But then I discovered the work of Frenchman Bernard Borrelly and his method "Coloriage virtuel" where he used these terms. So I kept track and anti-track. I find that network is the most appropriate term: TDP is a network method.
Cordialy
Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: How to call this pattern
Mauriès Robert wrote:Hi Space,
...
To end this discussion, because I think we have said everything about the essential
Not quite. I'd like to know why you insist on misspelling my handle. I'm sure you know how I interpret that. I've given you the benefit of the doubt so far, because I thought your translator program might do it. However, since it didn't happen in your early posts, and you're not taking my repeated hints now, I must finally ask.
Should I count you as one of my enemies here? That would be disappointing, because I thought we were in good terms despite our somewhat differing opinions. Then again, nothing surprises me any longer.
-SpAce-: Show
-

SpAce - Posts: 2671
- Joined: 22 May 2017
Re: How to call this pattern
Hi SpAce,
I am not your enemy, on the contrary I enjoy our discussions. If I wrote Space instead of SpAce, it was out of dizziness, nothing more.
I'll make sure I don't make the mistake again !
By the way, what does SpAce mean?
Robert
I am not your enemy, on the contrary I enjoy our discussions. If I wrote Space instead of SpAce, it was out of dizziness, nothing more.
I'll make sure I don't make the mistake again !
By the way, what does SpAce mean?
Robert
- Mauriès Robert
- Posts: 619
- Joined: 07 November 2019
- Location: France
Re: How to call this pattern
Hi Robert,
I'm very glad to hear that! I hope you understand that I've become a bit paranoid
Don't sweat about it. I only mind if I suspect (or know for sure) that it's done intentionally. I think it's a pretty cheap way to throw not-so-subtle insults.
I wish I could reply that I'm an astronaut, but unfortunately not (though at least one classmate of mine is). It's just a callsign I used a long time ago, in a galaxy far far away...
In the 90s I got hooked on a very different kind of game and almost certainly made an unbeatable world record in it. I used that handle in the related discussions with fellow players back then, and it got engraved in my class ring too.
I hadn't used it in any other context since then, but for nostalgic reasons I picked it for this. Perhaps I had ambitions to become as good a sudoku player as I was a star pilot. Not even close so far (and it will never happen either)
Mauriès Robert wrote:Hi SpAce,
I am not your enemy, on the contrary I enjoy our discussions. If I wrote Space instead of SpAce, it was out of dizziness, nothing more.
I'm very glad to hear that! I hope you understand that I've become a bit paranoid
I'll make sure I don't make the mistake again !
Don't sweat about it. I only mind if I suspect (or know for sure) that it's done intentionally. I think it's a pretty cheap way to throw not-so-subtle insults.
By the way, what does SpAce mean?
I wish I could reply that I'm an astronaut, but unfortunately not (though at least one classmate of mine is). It's just a callsign I used a long time ago, in a galaxy far far away...
In the 90s I got hooked on a very different kind of game and almost certainly made an unbeatable world record in it. I used that handle in the related discussions with fellow players back then, and it got engraved in my class ring too.
I hadn't used it in any other context since then, but for nostalgic reasons I picked it for this. Perhaps I had ambitions to become as good a sudoku player as I was a star pilot. Not even close so far (and it will never happen either)
-SpAce-: Show
-

SpAce - Posts: 2671
- Joined: 22 May 2017
13 posts
• Page 1 of 1

