The New Sudoku Players' Forum

[jim.ryan.63]

Can anyone please help me (a newbie here) understand how to solve the following partially completed puzzle? Thanks!
*-----------*
|892|576|413|
|467|321|985|
|531|984|276|
|---+---+---|
|973|6.2|85.|
|658|.3.|..2|
|124|85.|63.|
|---+---+---|
|..5|268|...|
|2.9|7.3|568|
|.86|.95|.2.|
*-----------*

[ReCiviliza]

You have to pencil in the possible values for each of the remaining cells after which the two empty cells in row 3, in column 4 and in block 8 all hold the same two potential values 1 & 4.

These 4 cells form an XY Chain from row 4 column 9 to row 9 column 4 in which a 4 at either end leads to a 1 at the other end so either r4c9 is 4 and r9c4 is 1 or r4c9 is 1 and r9c4 is 4. Since r9c9 sees both ends of the chain (ie a 1 & a 4) both of these values can be eliminated from r9c9 leaving 7 as the only possible value.

(Rather advanced for a Noob, I had to plug it into a solver to find this step, but anyway that is what is needed to break through at this point).

[Leren]

Code: Select all

*--------------------------------------*
| 8  9  2 | 5    7   6  | 4   1   3    |
| 4  6  7 | 3    2   1  | 9   8   5    |
| 5  3  1 | 9    8   4  | 2   7   6    |
|---------+-------------+--------------|
| 9  7  3 | 6   a14  2  | 8   5  b14   |
| 6  5  8 | 1-4  3   79 | 17  49  2    |
| 1  2  4 | 8    5   79 | 6   3   79   |
|---------+-------------+--------------|
| 37 14 5 | 2    6   8  | 137 49  1479 |
| 2  14 9 | 7    1-4 3  | 5   6   8    |
| 37 8  6 |d14   9   5  | 137 2  c147  |
*--------------------------------------*

The move in this solution is called a Skyscraper in cells a-b-c-d. It's easy to prove that one of cells a or d must be 4, so you can remove the 4's from r5c4 & r8c5 and the puzzle solves with singles from there.

You can read about Skyscrapers here.

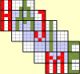
The previous post took a different approach, considering cells that have digits 14. The letters A & B in the following diagram refer to the "parity" of the 14 cells. A means that a 14 cell has one value (1/4 or 4/1) and B the other value (4/1 or 1/4).

Since r9c9 can see cells that have both parities A and B it can't be 1 or 4.

Code: Select all

*--------------------------------------*
| 8  9  2 | 5    7   6  | 4   1   3    |
| 4  6  7 | 3    2   1  | 9   8   5    |
| 5  3  1 | 9    8   4  | 2   7   6    |
|---------+-------------+--------------|
| 9  7  3 | 6   B14  2  | 8   5  A14   |
| 6  5  8 |A14   3   79 | 17  49  2    |
| 1  2  4 | 8    5   79 | 6   3   79   |
|---------+-------------+--------------|
| 37 14 5 | 2    6   8  | 137 49  1479 |
| 2  14 9 | 7    14  3  | 5   6   8    |
| 37 8  6 |B14   9   5  | 137 2  *7-14 |
*--------------------------------------*

Leren

[Hajime]

And the A&B method is called: 2-String Kite for candidate 1 and 4.

[SpAce]

And the A&B method is called: 2-String Kite for candidate 1 and 4.

True, it's a Dual 2-String Kite. More commonly it would be called a Remote Pair, though.

In general, Remote Pairs are both Dual X-Chains (Kite is a short X-Chain) as well as Dual XY-Chains (with just the same two values in every cell). The Dual X-Chain view is simpler (better) because it's much more efficient in terms of links, digits, and candidates used, even though both use the same cells. The difference is easy to see:

Dual X-Chain (2x2 strong links, 2x1 digits, 2x4 candidates):

Code: Select all

[(1)r9c4 = r5c4 - r4c5 = (1)r4c9] => -1 r9c9
[(4)r9c4 = r5c4 - r4c5 = (4)r4c9] => -4 r9c9

Dual XY-Chain (2x4 strong links, 2x2 digits, 2x8 candidates):

Code: Select all

[(1=4)r9c4 - (4=1)r5c4 - (1=4)r4c5 - (4=1)r4c9] => -1 r9c9
[(4=1)r9c4 - (1=4)r5c4 - (4=1)r4c5 - (1=4)r4c9] => -4 r9c9

The strong links in the cells are superfluous, making the flip-flopping XY-Chains unnecessarily long and complex.

Note that both of those options need two separate AICs to get both eliminations. Even some very experienced people have had the misconception that writing a Remote Pair as a single XY-Chain would somehow get both eliminations at once. That's not true at all. You need two different XY-Chains, just like you need two different X-Chains -- thus it's better to use the simpler X-Chains.

There's no easy way to write a Remote Pair as a single AIC to get both eliminations at once. Besides myself, not many people can do it correctly (or so I assume because I've never seen anyone else do it). In this case it's pretty simple ('.' in place of the standard '&' for better readability):

Code: Select all

[1r9c4.4r4c9 = 1r5c4|4r4c5 - 1r4c5|4r5c4 = 1r4c9.4r9c4] => -14 r9c9

[ghfick]

Hi Jim,
Welcome to the forum!
I recommend the solver YZF_Sudoku as a learning tool. Just for fun, I input your puzzle into YZF_Sudoku and then clicked on All Possible Steps.
The solver shows a wide range of steps that will complete or advance the puzzle. In addition to Skyscrapers, 2 String Kites and Remote Pairs, the solver illustrates steps called Empty Rectangles, W-Wings, a Uniqueness Test of Type 2, Finned X-Wings, Sashimi X-Wings and even more so-called 'Unfair' steps. Then the solver lists various chains and ALS steps. Then even more elaborate steps.
Of course, I would apply Occam's Razor in actual solving but it is interesting to see the wide range of options. Many with subtly different logic and many that are essentially the same logic.
You can get YZF_Sudoku from the forum's software section. The latest version is number 611.
Gordon

[SpAce]

Just for the record, this is the simplest way to write the RP(14)r4c9.r9c4 as a valid AIC:

Code: Select all

[(1,4,1,4 = 4,1,4,1)r4c95.r59c4] => -14 r9c9

It's relatively understandable, too.