http://forum.enjoysudoku.com/december-23-2014-t32232.html
I don't know what the source of it was, but it is one of the more interesting puzzles that I've come across in a long time- so thanks to Gurth.
- Code: Select all
*-----------*
|..9|..8|.2.|
|7..|...|...|
|...|.1.|8.6|
|---+---+---|
|..6|8..|.1.|
|...|.3.|..9|
|.4.|..6|2.8|
|---+---+---|
|315|.9.|.82|
|...|...|..1|
|.2.|3.1|4..|
*-----------*
- Code: Select all
*-----------------------------------------------------------------------------*
| 1456 356 9 | 4567 4567 8 | 1357 2 3457 |
| 7 3568 12348 | 24569 2456 23459 | 1359 3459 345 |
| 245 35 234 | 24579 1 234579 | 8 34579 6 |
|-------------------------+-------------------------+-------------------------|
| 259 3579 6 | 8 2457 24579 | 357 1 3457 |
| 1258 578 1278 | 12457 3 2457 | 567 4567 9 |
| 159 4 137 | 1579 57 6 | 2 357 8 |
|-------------------------+-------------------------+-------------------------|
| 3 1 5 | 467 9 47 | 67 8 2 |
| 4689 6789 478 | 2567 25678 257 | 35679 35679 1 |
| 689 2 78 | 3 5678 1 | 4 5679 57 |
*-----------------------------------------------------------------------------*
I expect to have to use nets to solve puzzles of difficulty above around ER=8.5, but below that I like to try to avoid them so this puzzle was solved with relatively simple chains: No nets (ie. AAICs/Krakens) and not even patterns (ie. empty rectangle, broken wings/guardians etc.) that often require net-like chains. It's possible that the solution could be further optimized, but I decided to stick with the first run.
A puzzle like this doesn't die easily so each chain may lead to one or more basic methods. I prefer to show those below the numbered chain that gave rise to them rather than number them individually. Fwiw: I don't see almost-hidden sets used on this forum that much. They are very useful constructs; two of them are used here.
1. (1)r2c3=(1-9)r2c7=r8c7-r8c2=r4c2-r4c6=(9-1)r6c4=(1)r5c4 => -1r5c3
2. (7)r5c2=aHP(79-3)r48c2=(3)r6c3 => -7r6c3
3. (1)r2c3=(1-3)r6c3=r6c8-r8c8=(3-9)r8c7=(9)r2c7 => -1r2c7
=> singles: r2c3=1,r1c7=1,r2c2=8,r6c3=3
=> LCs: –6r1c45, -2r3c46 np(57)r6c58 -> -5r6c14,-7r6c4
=> grp skyscraper: (7)c4568r36 => -7r1c5
4. grp(9)r3c46=r3c8-r9c8=r9c1-r6c1=(9)r6c4 => -9r2c4
5. als(459=3)r2c789-r2c6=r3c6-(3=5)r3c2-als(5=79)r45c2-(9)r6c1=r6c4-als(9=457)r3c6,r1c45 => -45r2c456
=> np(26)r2c45 => -2r2c6
=> LCs: -45r1c9, -45r3c8
6. (3)r4c7=(3-4)r4c9=(4-6)r5c8=grp(6)r89c8-(6=7)r7c7 => -7r4c7
7. pausingchn(4=7)r7c6-(7=6)r7c7-r5c7=(6-4)r5c8=*(4)r4c9-r4c5=(4)r1c5 => -4r34c6
8. (3=5)r4c7-r6c8=r6c5-(4=5)r1c5-r4c5=(4)r4c9 => -3r4c9
=> singles: r4c7=3, r8c8=3
=> xy-wing: (79)r3c8[(59)r2c7,(57)r6c8] => -5r1c8,-5r5c7
=> np(67)r57c7 => -67r8c7
9. (7)r1c4=(7-3)r1c9=(3-4)r2c9=r4c9-r4c5=(4)r1c5 => -4r1c4
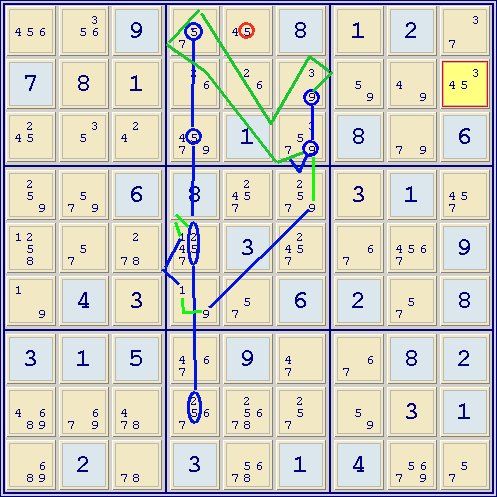
10. grp(5)r13c4=aHP(25-1)r58c4=(1-9)r6c4=(9-4)r3c4=(4)r1c5 => r1c5<>5=4 -> r4c9=4
=> nt(356)box1 => -5r3c1
=> nt(567)r5c278: -5r5c146, -7r5c346
=> LCs: -7r8c2, -5r9c8
11. (9=1)r6c4-als(1=24)r5c46-(2=8)r5c3-(8=7)r9c3-r9c9=r1c9-(7=9)r3c8 => -9r3c4
stte
Step 10 was a critical step and uses an almost-hidden pair. For those that might be interested:
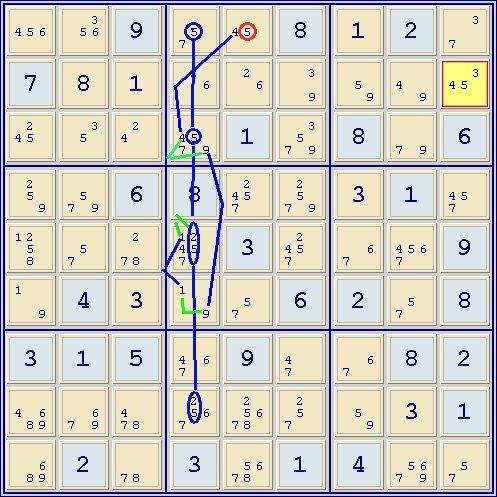
Below: Alternative end of step 10: grp(5)r13c4=aHP(25-1)r58c4=(1-9)r6c4=r4c6-als(9=357)r1c4,r23c6