A house is a collection of 9 cells that must hold all digits 1 to 9 exactly once.
When 2 or more houses intersect, they share one or more cells.
The most well known intersection of 2 houses is the row (or column) intersection with a box.
- GI.png (32.8 KiB) Viewed 1441 times
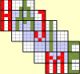
In the picture above and the examples below all candidates are a "1" and cells where no "1" is present are noted as "/".
Cells with a candidate "1" that are not possible to have a "1", will be striked through.
Cells with no value (empty cells) are irrelevant to the subject, but may even contain a candidate 1.
Example 1 pointing or box-line reduction
A candidate 1 of a cell is the possible digit 1 can be the solution of that cell.
In above example in box 1 there are 2 cells with possible candidate 1 in row 3.
Because nowhere else in the box 1 can be a solution one of the 2 cells must be a 1.
And that leads to the conclusion that everywhere else in row 3 all cells with candidate 1 can eliminate 1, except for the 2 cells in common.
Example 2 claiming or line-box reduction
Also the other way around when 2 or 3 cells in row 7 AND box 9 have candidate 1 and no other cell in row 7 holds a 1, all other cells outside the intersection of box 2 can eliminate candidate 1.
Because a intersection between a row and a column is just 1 cell, than if eg the row holds only candidate k in that intersection cell, it would be the only candidate k in that row, and it would be a hidden or naked single.
In a normal Sudoku with rows, columns and boxes the above 2 methods to eliminate candidates are the only possible intersection methods.
In stead of 2 cells in the intersection between a box and a column or row may also be 3 cells with candidate k.
In a Windoku, Asterisk, SudokuX, etc more intersection methods are possible.
General rule:
If a house H has all cells with candidate k trapped/locked in the intersections with other houses then all cells outside H that 'see' all cells with k of H can eliminate k.
A common cell in ALL the houses of a collection is not necessary, but each house needs intersection with each other house.
Example 3 Windoku: Wbox to row
Wbox 2 has candidate 1 in row 3 and nowhere else. So row 3 can eliminate all other candidates 1 outside W2.
Example 4 Asterisk: asterisk to row
Row 3 has all its candidates in Asterisk. All other cells in Asterisk can eliminate candidate 1.
Above all intersections deals with intersections of 2 houses,
but with 3 or more houses we have to deal with 'Generalized Intersections'
An Asterisk, Girandola or CenterDots holds 1 extra house.
A SudokuX holds 2 extra houses, the diagonals.
A Windoku or SudokuP holds 9 extra houses (see picture between example 3 and 5).
Example 5 a row a column and a diagonal
Row 3 says 'all my candidates 1 are within a column and a diagonal'.
There is no cell that is part of all 3 houses. This is not necessary.
We can eliminate candidate 1 from cells that are part of column and diagonal that 'see' all 2 candidates of row 3.
So r6c6<>1.
The houses must intersect to each other. If some houses do not intersect you can split up the houses in 2 separate problems.
Split up non-intersecting houses picture between example 4 and 6.
Row 4 and row 6 do intersect with box 4 but do not intersect with each other.
You can split up "the problem" with 2 smaller problems: 1: row 4 with box 4 and 2: row 6 with box 4.
It is not necessary that there is 1 common same cell in all the houses. see example 5 and 6.
Example 6 two diagonals and 1 row
The first diagonal says 'that all my candidates 1 are in the intersections of the other diagonal and row 3'.
Now the cell that 'sees' those two cells and is outside the first diagonal can eliminate candidate 1.
So r3c7<>1.
Example 7 hidden W, box and column
This is an encountered example, described in http://forum.enjoysudoku.com/windoku-and-xy-chain-t37966.html
Box 1 has all its candidates 1 locked in intersections with W5 and c3.
r5c3 'sees' all these cells with candidate 1 and cannot have a 1.
So r5c3<>1.
Example 8 row, column and Asterisk
The Asterisk says that all its cells with candidate 1 are in row 2 and column 2.
r3c2 'sees' all those cells and cannot be a 1.
So r3c2 <> 1.
Example 9 Asterisk, Windoku and Diagonal
Another example with a Diagonal and an Asterisk and Windoku-box 1.
The \-diagonal says that all its candidate 1 cells are in the intersections with W1 and A.
All cells in W1 and A that see those locked cells are r2c5 and r5c2, which can not hold candidate 1.
All locked cells are in W1 but also in b1 (normal box 1), but it is not a 4-houses problem.
You have 2 solutions for the same situation, the W1 of b1 variant, both are a 3-houses problem.
Above several intersections with 3 houses, but it can be even 4 or more.
Example 10 with 4 intersecting houses.
An Asterisk, Diagonal, a row and a column.
The Asterisk says 'all my candidates 1 are locked in cells within intersections of r2, c8 and the /-diagonal'.
Cell r2c8 'sees' all the 4 locked Asterisk cells with candidates 1, so this r2c8 cannot hold candidate 1.
Creation of a 4-house intersection problem is not that simple. So I appreciate if other examples of 4 (and 5) intersecting houses will be posted.
