sis: strong inference set. A set of boolean conditions such that at least one item in the set must be true.
Often, I derive a more powerful intermediate set such that exactly one item in the set must be true. These are what I now call "quantum cells". These sets are very valuable, as they plug into existing deduction methods without any thought involved.
We are, in both our approaches, attacking the same puzzle areas. I mentally "tag" chunks of relationships. You seem to tag more finely, with more detail. I let the "chunks" contain the fine detail without using the details until they are useful. For example, an "almost" continuous net derives an entire set of relationships - both weak and strong - that can be used later at will. This is analagous to ALS, and AC, except perhaps that it is never limited by simple units in sudoku, but rather driven by logical chunks in the particular puzzle.
Full Tagging
45 posts
• Page 3 of 3 • 1, 2, 3
Steve K wrote:sis: strong inference set. A set of boolean conditions such that at least one item in the set must be true.
Often, I derive a more powerful intermediate set such that exactly one item in the set must be true. These are what I now call "quantum cells". These sets are very valuable, as they plug into existing deduction methods without any thought involved.
Regarding "sis", I was far from the truth.
Although the rules I used for derived weak inferences could be applied to 'sis', I never use them. I am strictly limited to 'choices' or 'quantum cells' (we have strictly the same definition for that object.
I need now another precise definition to go ahead in the reading
Steve K wrote:We are, in both our approaches, attacking the same puzzle areas. I mentally "tag" chunks of relationships. You seem to tag more finely, with more detail. I let the "chunks" contain the fine detail without using the details until they are useful.
What is precisely a chunk?
Regarding fine tagging, in my process, the tag (a container for binary entities being all TRUE or all FALSE in the solution) is the basis for stockpiling of weak links(weak inferences).
To each tag is associated a binary field linking to other tags. If a weak link is identified, the bit is set to 1. This is likely equivalent to your 'memory function'
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
Steve,
I did my best to enter the second part of your solution to strm puzzle, but I have to confess I failed.
The path is brilliant, and I think they are few that can read ant catch your post. I had several reasons to give up.
I am lacking appropriate background to follow you,
It seems you are intensively using uniqueness and symmetry (in that case), both are far from my process.
What I am doing is basic. No great theory, just a small number of rules making a consistent set solving all known puzzles.
Practice has shown that for hardest puzzles, the path was long and most often boring. Consequently I am looking for improvements closer to what a player can achieve.
What is interesting for me in my last idea is that the ‘scenario analysis’ concept can be applied to the basic stuff (bi values including groups). If you can show that a couple of ‘basic’ tags is not valid, you have identified a new weak inference, opening doors for new AICs.
Normally this should change the border between my levels.
I am still interested in understanding how you select your MBM and what you keep in memory when you have identified one. This is likely the central point in your process. On my side, tagging is the key process for easy puzzles; analysis of choices / Quantum cells is the complementary step.
I did my best to enter the second part of your solution to strm puzzle, but I have to confess I failed.
The path is brilliant, and I think they are few that can read ant catch your post. I had several reasons to give up.
I am lacking appropriate background to follow you,
It seems you are intensively using uniqueness and symmetry (in that case), both are far from my process.
What I am doing is basic. No great theory, just a small number of rules making a consistent set solving all known puzzles.
Practice has shown that for hardest puzzles, the path was long and most often boring. Consequently I am looking for improvements closer to what a player can achieve.
What is interesting for me in my last idea is that the ‘scenario analysis’ concept can be applied to the basic stuff (bi values including groups). If you can show that a couple of ‘basic’ tags is not valid, you have identified a new weak inference, opening doors for new AICs.
Normally this should change the border between my levels.
I am still interested in understanding how you select your MBM and what you keep in memory when you have identified one. This is likely the central point in your process. On my side, tagging is the key process for easy puzzles; analysis of choices / Quantum cells is the complementary step.
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
Champagne: After struggling with EM, I learned a few valuable lessons about puzzles that contain the hidden pair loop - or whatever it should be called. Specifically, such puzzles will require the consideration of too many sis to achieve a single elimination. Thus, the obvious path was to stop looking for eliminations, but rather to look for pieces of information that were easily remembered. The absurd symmetry of that class of puzzles leads to many similar deductions. Thus, it seems wise to use the symmetry of the puzzle. In strm's puzzle, finding the correct relationship between (39) in box 1 and (39) in box 9 is difficult, but once found the puzzle is almost easy.
I value highly using almost continuous networks as "chunks", as they have mutiple weak links emanating from them and they are easy to use in deductions, as they form a very specific pattern. In fact, they act quite a bit like "cells" or quantum groups themselves, except that they are "almost" groups.
They are closely related to uniqueness considerations, in theory. I have not yet been quite able to make the leap to producing meaningful uniqueness theorems from them in practice. Nevertheless, continuous networks can only overlap so much in a puzzle before either a no solution, or a multiple solution situation must occur. Thus, almost continuous networks eventually can "fill" a puzzle.
The long arduous process of unlocking these beasts is made less long and boring once one stops looking for immediate eliminations, and instead searches for quantums, imo. The quantums are most easily proven using almost continuous networks, thus the choice of using them is specifically directed towards finding quantums.
Whether our approaches are quite different or not I am not sure of. I do know, however, that we seem to attack much the same puzzle areas.
I value highly using almost continuous networks as "chunks", as they have mutiple weak links emanating from them and they are easy to use in deductions, as they form a very specific pattern. In fact, they act quite a bit like "cells" or quantum groups themselves, except that they are "almost" groups.
They are closely related to uniqueness considerations, in theory. I have not yet been quite able to make the leap to producing meaningful uniqueness theorems from them in practice. Nevertheless, continuous networks can only overlap so much in a puzzle before either a no solution, or a multiple solution situation must occur. Thus, almost continuous networks eventually can "fill" a puzzle.
The long arduous process of unlocking these beasts is made less long and boring once one stops looking for immediate eliminations, and instead searches for quantums, imo. The quantums are most easily proven using almost continuous networks, thus the choice of using them is specifically directed towards finding quantums.
Whether our approaches are quite different or not I am not sure of. I do know, however, that we seem to attack much the same puzzle areas.
- Steve K
- Posts: 98
- Joined: 18 January 2007
Steve K wrote:Champagne: After struggling with EM, I learned a few valuable lessons about puzzles that contain the hidden pair loop - or whatever it should be called.
I guess you are speaking of puzzles having the SK loop. This is a nickname everybody can catch.
In that family some are relatively easy as that one, included in my sample file.
- Code: Select all
Coloin 02805 in gsf list
600000002090400050001000700050943000000105000000800040007000600030009080200000001
Nevertheless, I could not solve it with level 3 of my process. I have no experience of a puzzle having the SK loop that could be solved with my level 3.
Steve K wrote:Specifically, such puzzles will require the consideration of too many sis to achieve a single elimination. Thus, the obvious path was to stop looking for eliminations, but rather to look for pieces of information that were easily remembered. . . .
I value highly using almost continuous networks as "chunks", as they have mutiple weak links emanating from them and they are easy to use in deductions, as they form a very specific pattern. In fact, they act quite a bit like "cells" or quantum groups themselves, except that they are "almost" groups.
It seems to me that we have similarities between processes based on sis and processes based on nets of AICs. In both cases, you know that you can solve any puzzle applying the process to any native entity fitting with the process(sis or strong/weak inferences). It has been proven with sis, I suspect it is true as well with AICs nets if you add an extended view of scenario analysis. The problem is that the result is something a player can not achieve.
As you, if there is no direct elimination thru a single AIC, I am looking for pieces of information. In my case, a piece of information is always a new weak link (weak inference).
Elementary net (AICs applied to a choice/quantum cell) is used when it shows a new weak inference,
Killing a super candidate in a AALS/AAHS/AC2 leads to a weak inference,
The last pattern I posted leads to a new weak inference as well.
Steve K wrote:The absurd symmetry of that class of puzzles leads to many similar deductions. Thus, it seems wise to use the symmetry of the puzzle. In strm's puzzle, finding the correct relationship between (39) in box 1 and (39) in box 9 is difficult, but once found the puzzle is almost easy.
In all puzzles having the SK loop but one, my solver found immediately the necessary logic to establish existing properties similar to that one. It’s not done working explicitly on symmetries, but on AALS/AAHS/AC2. For sure, the sequence of ‘virus patterns’ in the SK loop is part of that quick finding, so indirectly, the symmetry plays a key role..
Steve K wrote:They are closely related to uniqueness considerations, in theory. I have not yet been quite able to make the leap to producing meaningful uniqueness theorems from them in practice. Nevertheless, continuous networks can only overlap so much in a puzzle before either a no solution, or a multiple solution situation must occur.
I never used the ‘multiple solutions’ stop. The ‘no solution’ always comes (may be later), and looking for ‘multiple solution’ patterns is not so easy.
Steve K wrote:Whether our approaches are quite different or not I am not sure of. I do know, however, that we seem to attack much the same puzzle areas.
Whatever is the process used, we are looking for short sequences and using limited sets of tools. No surprise if we fight against the same weaknesses of puzzles.
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
Nothing new for long in the field of hardest puzzles, so I worked to improve the basic process to meet somehow the impressive performance of human players on “very difficult” puzzles.
In the basic process, the general strategy is to look for the path of easiest clearings and moves. When the tagging leads to a clearing of candidates, the process restarts immediately at the search of basic moves.
On tough puzzles, human players do more. They find short paths, very often thru a T&E process, but most often, the corresponding forcing chain is equivalent to a net of AICs.
I changed the strategy in the tagging process on three main points:
This is not a process as pure as the basic one. Selecting the “most efficient” clearings requires the knowledge and the use of the final solution. There is also a limit in the forecast of the consequences of a clearing. An optimized forecast would request a simulation of the clearing process excluding tagging. This is not done here. The solver sees only what is granted thru AICs nets.
I used the following set of puzzles as test file.
These are puzzle prepared by JPF selected, as far a I Know, in the range of SE 9 -9.5. The have been published on a French forum, so I know how human players solved them.
All the puzzles where solved in that limited process, The overall print switched from 259K to 109K (including temporary messages for testing purpose) giving a rough idea of improvements. The processing time has been higher (except in one case), but I suspect that the introduction of scenarios is responsible for the main part of that change.
Here after is a table summarizing the changes:
Col 2 3 time(seconds) and print size in the new process
Col 4 5 same in the basic process.
Detailed solutions with the new process will come in the thread “full tagging examples”. We will see a one shot cracking (277H), paths including scenarios (not so many) and one case where, in the limits I authorized, the solver made a step leading to no new known cell.
We are still far from some clearing made by human solver. The stuff used is too limited
For tougher puzzles, the same process will be applied including ALS AHS. Both clearing power and forecast quality will be improved in that new step.
Another point is to switch from blind scenarios to intelligent ones. Super candidates for AC2 is an example of intelligent scenario. It has been proven very efficient.
Analyzing the “human” paths for such puzzles, I have the feeling that with the set including ALS AHS/ACS we have some intelligent scenarios to consider. This could come later..
In the basic process, the general strategy is to look for the path of easiest clearings and moves. When the tagging leads to a clearing of candidates, the process restarts immediately at the search of basic moves.
On tough puzzles, human players do more. They find short paths, very often thru a T&E process, but most often, the corresponding forcing chain is equivalent to a net of AICs.
I changed the strategy in the tagging process on three main points:
- Code: Select all
I start derived weak links at level one (using exclusively bi values including groups, no ALS AHS . . ),
I search in priority clearings leading to new known positions in the puzzle,
I introduce as new tags in a blind mode all scenarios combining two tags of the level one stuff.
This is not a process as pure as the basic one. Selecting the “most efficient” clearings requires the knowledge and the use of the final solution. There is also a limit in the forecast of the consequences of a clearing. An optimized forecast would request a simulation of the clearing process excluding tagging. This is not done here. The solver sees only what is granted thru AICs nets.
I used the following set of puzzles as test file.
- Code: Select all
012000000030000400500167000080004007000050000100200060000623005009000020000000140_278H
012000304400010000000004002004000560000070000083000200800700000000040009906000480_277H
012000030040250060700000400300800000500070008000009006009000004060091050050000790_276H
001000000234500000006370000005000006800090007100000200000083100000002458000000600_275H
000120003000000400005006000000070021081040560250080000000800300006000000400037000_274H
000102300400000005060070000600005002070040010300800004000080020800000009005609000_273H
100020030040005001000000500000600070801000209030009000005000000300800010090040006_272H
100000230000301000040500600070000084000090000830000010007004060000102000016000003_271H
010234050000000000005000600000600027800010003470009000006000200000000000090583010_270H
These are puzzle prepared by JPF selected, as far a I Know, in the range of SE 9 -9.5. The have been published on a French forum, so I know how human players solved them.
All the puzzles where solved in that limited process, The overall print switched from 259K to 109K (including temporary messages for testing purpose) giving a rough idea of improvements. The processing time has been higher (except in one case), but I suspect that the introduction of scenarios is responsible for the main part of that change.
Here after is a table summarizing the changes:
Col 2 3 time(seconds) and print size in the new process
Col 4 5 same in the basic process.
- Code: Select all
278H 1.2 12K 0.2 22K
277H 0.0 3K 0.1 11K
276H 0.3 9K 0.2 26K
275H 1.9 10K 0.2 25K
274H 0.9 14K 0.4 33K
273H 1.0 14K 0.8 43K
272H 2.4 17K 0.6 38K
271H 1.3 18K 0.6 37K
270H 0.6 7K 0.2 19K
av 1.1 0.4.
Detailed solutions with the new process will come in the thread “full tagging examples”. We will see a one shot cracking (277H), paths including scenarios (not so many) and one case where, in the limits I authorized, the solver made a step leading to no new known cell.
We are still far from some clearing made by human solver. The stuff used is too limited
For tougher puzzles, the same process will be applied including ALS AHS. Both clearing power and forecast quality will be improved in that new step.
Another point is to switch from blind scenarios to intelligent ones. Super candidates for AC2 is an example of intelligent scenario. It has been proven very efficient.
Analyzing the “human” paths for such puzzles, I have the feeling that with the set including ALS AHS/ACS we have some intelligent scenarios to consider. This could come later..
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
Thanks to Allan Barker and it’s brilliant solution to Fata Morgana than you can find
http://forum.enjoysudoku.com/viewtopic.php?t=6353&postdays=0&postorder=asc&start=0&sid=23900beca78a6c7fbad7518fb63d6522
I have a potential improvement of the level 4 logic.
The new point at level 4 is introduction of AC2s a group of n cells with n+x digits and n-2 compulsory digits.
For practical reasons, I limited the groups to those having n+2 digits.
A super candidate is any couple of digit that can fill the group.
So in fact, an AC2 can have up to six super candidates.
I missed a degenerated form of AC2, a group like r1c1=123;r1c2=123.
That one has only 3 super candidates, but it can be fitted with most of the AC2 logic. It can, as a limit, participate to a virus pattern analysis.
I like the idea to introduce this stuff in the scope of level 4 because it is not an increase in overall difficulty.
Processed as a “degenerated” AC2, it should no require much additional code and would give a higher solving potentiality.
champagne
http://forum.enjoysudoku.com/viewtopic.php?t=6353&postdays=0&postorder=asc&start=0&sid=23900beca78a6c7fbad7518fb63d6522
I have a potential improvement of the level 4 logic.
The new point at level 4 is introduction of AC2s a group of n cells with n+x digits and n-2 compulsory digits.
For practical reasons, I limited the groups to those having n+2 digits.
A super candidate is any couple of digit that can fill the group.
So in fact, an AC2 can have up to six super candidates.
I missed a degenerated form of AC2, a group like r1c1=123;r1c2=123.
That one has only 3 super candidates, but it can be fitted with most of the AC2 logic. It can, as a limit, participate to a virus pattern analysis.
I like the idea to introduce this stuff in the scope of level 4 because it is not an increase in overall difficulty.
Processed as a “degenerated” AC2, it should no require much additional code and would give a higher solving potentiality.
champagne
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
Back to the topic of “super candidates” or paired candidates to use the preferred name of strmckr.
Looking at solutions proposed by manual players, pushed by strmckr and finally forced to see that Fata Morgana has a relatively easy solution, I have to fill a gap. I already gave the general idea. I will present it slightly differently here.
A super candidate is a couple of two candidates or groups of candidates than can “solve a specific pattern”
If we have candidates r1c1=456;r1c2=456 we have three possible “super candidates”:
{4r1c12 & 5r1c12}; {4r1c12 & 6r1c12}; {5r1c12 & 6r1c12}
Each of these “super candidates” also named “couple tags” in previous posts behave in AICs strictly as candidates.
If we want to go from easiest to toughest pattern we could say:
r1c1=45 r1c2=45 is a pattern with 1 super candidate
r1c1=456 r1c2=456 is a pattern with 3 super candidates
r1c1=4567 r1c2=4567 is a pattern with 6 super candidates.
In Sudoku, we always have a corresponding “hidden pattern”.
If two digits can only be located in two cells, this is a hidden super candidate.
If two digits are locked in three cells, we have three ways to combine the cells to form “super candidates”
If two digits are locked in four cells, we have six ways to combine the cells.
We could increase the difficulty either as suggests strmckr considering three candidates, or choosing 2candidates out of 5;6 but the difficulty grows rapidly .
For historical reasons, I started “super candidates” logic on AC2, a pattern with 6 super candidates.
I was preparing the processing of a hidden pattern with three super candidates when came Fata Morgana raising an overall priority which was to figure out why the solver failed.(mainly when Allan announced he could solve it easily).
The reason why I chose a hidden pattern is very simple. An AHS/AC with three cells (two compulsory digits) is a stuff I was already processing. I had the feeling, analyzing some players’ proposals to solve puzzles, that super candidates handling would add something to my process in terms of speed.
I have now to add the pattern with two cells having in total three digits as candidates. My first idea was to consider them as degenerated AC2 (previous post). I am now more in favor of creating something as level 4a and level 4b, one limited to patterns having three super candidates, one for patterns having 6 super candidates.
BTW, I see what can be the “hidden pattern” with 6 super candidates, but it is still for me a virgin field.
champagne
Looking at solutions proposed by manual players, pushed by strmckr and finally forced to see that Fata Morgana has a relatively easy solution, I have to fill a gap. I already gave the general idea. I will present it slightly differently here.
A super candidate is a couple of two candidates or groups of candidates than can “solve a specific pattern”
If we have candidates r1c1=456;r1c2=456 we have three possible “super candidates”:
{4r1c12 & 5r1c12}; {4r1c12 & 6r1c12}; {5r1c12 & 6r1c12}
Each of these “super candidates” also named “couple tags” in previous posts behave in AICs strictly as candidates.
If we want to go from easiest to toughest pattern we could say:
r1c1=45 r1c2=45 is a pattern with 1 super candidate
r1c1=456 r1c2=456 is a pattern with 3 super candidates
r1c1=4567 r1c2=4567 is a pattern with 6 super candidates.
In Sudoku, we always have a corresponding “hidden pattern”.
If two digits can only be located in two cells, this is a hidden super candidate.
If two digits are locked in three cells, we have three ways to combine the cells to form “super candidates”
If two digits are locked in four cells, we have six ways to combine the cells.
We could increase the difficulty either as suggests strmckr considering three candidates, or choosing 2candidates out of 5;6 but the difficulty grows rapidly .
For historical reasons, I started “super candidates” logic on AC2, a pattern with 6 super candidates.
I was preparing the processing of a hidden pattern with three super candidates when came Fata Morgana raising an overall priority which was to figure out why the solver failed.(mainly when Allan announced he could solve it easily).
The reason why I chose a hidden pattern is very simple. An AHS/AC with three cells (two compulsory digits) is a stuff I was already processing. I had the feeling, analyzing some players’ proposals to solve puzzles, that super candidates handling would add something to my process in terms of speed.
I have now to add the pattern with two cells having in total three digits as candidates. My first idea was to consider them as degenerated AC2 (previous post). I am now more in favor of creating something as level 4a and level 4b, one limited to patterns having three super candidates, one for patterns having 6 super candidates.
BTW, I see what can be the “hidden pattern” with 6 super candidates, but it is still for me a virgin field.
champagne
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
Super Candidates in a “3 super candidates” pattern
I introduce that new property and it did not prove to be efficient.
Historically, super candidates has been introduced in my solver as possible solutions for AC2.
Each AC2 has six possible super candidates.
Studying FATA MORGANA puzzle, I thought it could happen that considering patterns with three super candidates would help to solve that puzzle.
I identified two patterns with three super candidates:
123 two cells with three candidates
12+ 12+ 12+ three cells in which two candidates are locked.
Compared to patterns with six super candidates, pattern with 3 super candidates have a strong advantage. If a super candidate is proven invalid, then, some candidates can always be cleared.
The implementation of this case is consequently much simpler that for AC2.
I got poor (if any) results from these new tags. I see two reasons:
“3 super candidates” patterns are not a high frequency,
Often , we have downgraded patterns in full redundancy with existing tagging.
May be also that hidden redundancy is much higher than I expected.
I need more experimentation to come to a final position, but for the time being, this is a very disappointing addition.
Looking at “ttt”s solutions (and also solutions form others players), I feel I would have more satisfaction adding some deadly patterns recognition. May be I’ll some step in that direction in parallel to Allan Barker method implementation.
I introduce that new property and it did not prove to be efficient.
Historically, super candidates has been introduced in my solver as possible solutions for AC2.
Each AC2 has six possible super candidates.
Studying FATA MORGANA puzzle, I thought it could happen that considering patterns with three super candidates would help to solve that puzzle.
I identified two patterns with three super candidates:
123 two cells with three candidates
12+ 12+ 12+ three cells in which two candidates are locked.
Compared to patterns with six super candidates, pattern with 3 super candidates have a strong advantage. If a super candidate is proven invalid, then, some candidates can always be cleared.
The implementation of this case is consequently much simpler that for AC2.
I got poor (if any) results from these new tags. I see two reasons:
“3 super candidates” patterns are not a high frequency,
Often , we have downgraded patterns in full redundancy with existing tagging.
May be also that hidden redundancy is much higher than I expected.
I need more experimentation to come to a final position, but for the time being, this is a very disappointing addition.
Looking at “ttt”s solutions (and also solutions form others players), I feel I would have more satisfaction adding some deadly patterns recognition. May be I’ll some step in that direction in parallel to Allan Barker method implementation.
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
HI,
Happy christmas to all.
Just taking that opportunity to say that now the solver has integrated
Allan Barker model complementary to tagging when tagging fails
Symmetry
and that should come quickly
Extended RI capabilities
and (I hope) later some additional possibilities on
Almost fish patterns
documentation on the first 2 item can be found on my web site in this book
http://pagesperso-orange.fr/gpenet/UM/UM00
Now again, all known puzzles can be solved by the solver, but use of Allan Barker model forces that conclusion. For the time being, use of Allan's model is limited to "Fata Morgana" and "Trompe L'Oeil", 2 puzzles from tarek.
champagne
Happy christmas to all.
Just taking that opportunity to say that now the solver has integrated
Allan Barker model complementary to tagging when tagging fails
Symmetry
and that should come quickly
Extended RI capabilities
and (I hope) later some additional possibilities on
Almost fish patterns
documentation on the first 2 item can be found on my web site in this book
http://pagesperso-orange.fr/gpenet/UM/UM00
Now again, all known puzzles can be solved by the solver, but use of Allan Barker model forces that conclusion. For the time being, use of Allan's model is limited to "Fata Morgana" and "Trompe L'Oeil", 2 puzzles from tarek.
champagne
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
Champagne,
Congratulations, and Merry Christmas to all.
I just found a new theory today. I was surprised when it found the following logic:
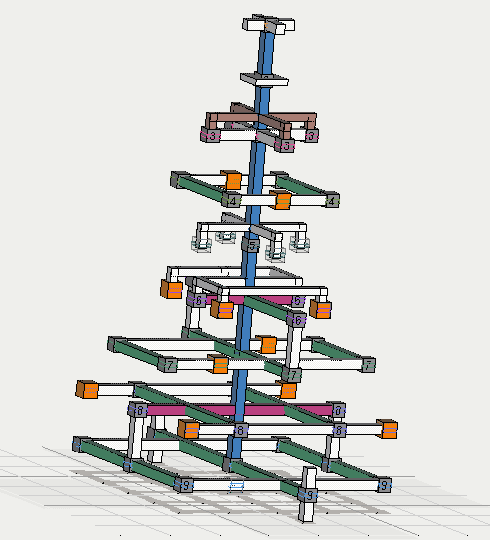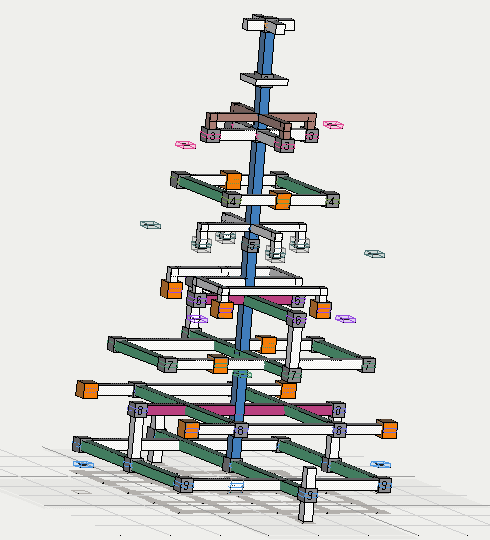
(I will change this to a thumb tomorrow)
Allan
Congratulations, and Merry Christmas to all.
I just found a new theory today. I was surprised when it found the following logic:

(I will change this to a thumb tomorrow)
Allan
- Allan Barker
- Posts: 266
- Joined: 20 February 2008
I made recently important changes in the solver.
I try here to summarize the situation.
Most of the changes done or to come refer to new things found and described in these threads:
Bi bi patterns in hardest puzzles
http://forum.enjoysudoku.com/viewtopic.php?t=6546
More Monster Loops, Structure and Symmetry
http://forum.enjoysudoku.com/viewtopic.php?t=6556
AIC’s nets equivalent to forcing nets
http://forum.enjoysudoku.com/viewtopic.php?t=6444
Basically what has been done is:
1) Introduction of the bi-bi and Exocet patterns in the process,
2) Limitation of AC2 processed to virus patterns
3) Limitation of AC to 3 cells patterns
4) Direct handling of virus pattern chains
5) Introduction of UR patterns in AIC’s nets
6) Revision of the main clearing process
In fact, the code related to AC2, virus pattern, vicinity analysis, pattern with 3 super candidates has been completely reworked from nil.
2 main targets in those changes:
a) Looking for simpler solutions generally speaking,
b) Getting the best from Exocet patterns.
Results are pretty good, but after so many changes, a full test campaign has to be planned. Working on hardest puzzles, analysis of a print is a heavy task, so the final validation will take time. The easiest part, cleaning all bugs leading to false eliminations, is over,
Points 2) and 3) intend to produce shorter solutions focusing on stuff easily detected by a player. Results are pretty good with the noticeable exception of Golden Nugget and Silver Plate. Without Exocet and with the reduced lot of AC2, these two puzzles could not be solved without use of Allan Barker model.
Including Exocets, all the puzzles where solved without use of Allan Barker model, most often with a remarkable collapse in runtime and print size.(divided by 5 on both parameters for Golden Nugget).
The scan for bi bi patterns remains for the time being an exhaustive scan. Focusing on specific patterns will come later;
UR patterns handling is still far from what “ttt” and others are doing, Only simplest cases are coded;
Limiting the number of AC included in the process forced a complete revision of virus pattern chains handling. SK loop is now searched at level 4 of the process prior to tagging, in a direct processing of Virus pattern chains. Also, in the tagging process, all consequences of virus pattern chains are analyzed (formerly, there was some redundancy with the tagging process done out of all AC2 ). The virus pattern chaining is now a key process.
Vicinity analysis has been as well completely reshaped and extended to Exocet patterns scenario analysis.
Regarding Exocets patterns (at least for the forms already integrated in the process), The split of each super candidate in 2 scenario is now fully operational and again, the maximum has been done to improve the vicinity analysis.
Are missing now the last findings in the linked threads as:
1)Platinum Blonde Exocet specific pattern ,
2)Mini Row pattern found by ronk and Allan Barker,
3)And somehow some new ideas to extract from Ronk and Allan rank 0 SLGs offering a huge number of eliminations.
In that last case, may be the best way is to stick to Allan Barker model, That model is for the time being a kind of escape lane in my solver, mainly because the mix of both logics is not very easy. I will nevertheless study whether there is an equivalent process closer to the main logic in the tagging process;
Another problem to face is handling of huge lots of “hardest” puzzles.
I run thousands of puzzles mainly produced by coloin, but not only, to evaluate the difficulty as seen by the solver.
For the time being, I sort the results using the bloc-notes, which is not performing very well. I must organize the process to have a sorting capability if I want to be in a position to analyze a significant database.
Still a lot to do
champagne
I try here to summarize the situation.
Most of the changes done or to come refer to new things found and described in these threads:
Bi bi patterns in hardest puzzles
http://forum.enjoysudoku.com/viewtopic.php?t=6546
More Monster Loops, Structure and Symmetry
http://forum.enjoysudoku.com/viewtopic.php?t=6556
AIC’s nets equivalent to forcing nets
http://forum.enjoysudoku.com/viewtopic.php?t=6444
Basically what has been done is:
1) Introduction of the bi-bi and Exocet patterns in the process,
2) Limitation of AC2 processed to virus patterns
3) Limitation of AC to 3 cells patterns
4) Direct handling of virus pattern chains
5) Introduction of UR patterns in AIC’s nets
6) Revision of the main clearing process
In fact, the code related to AC2, virus pattern, vicinity analysis, pattern with 3 super candidates has been completely reworked from nil.
2 main targets in those changes:
a) Looking for simpler solutions generally speaking,
b) Getting the best from Exocet patterns.
Results are pretty good, but after so many changes, a full test campaign has to be planned. Working on hardest puzzles, analysis of a print is a heavy task, so the final validation will take time. The easiest part, cleaning all bugs leading to false eliminations, is over,
Points 2) and 3) intend to produce shorter solutions focusing on stuff easily detected by a player. Results are pretty good with the noticeable exception of Golden Nugget and Silver Plate. Without Exocet and with the reduced lot of AC2, these two puzzles could not be solved without use of Allan Barker model.
Including Exocets, all the puzzles where solved without use of Allan Barker model, most often with a remarkable collapse in runtime and print size.(divided by 5 on both parameters for Golden Nugget).
The scan for bi bi patterns remains for the time being an exhaustive scan. Focusing on specific patterns will come later;
UR patterns handling is still far from what “ttt” and others are doing, Only simplest cases are coded;
Limiting the number of AC included in the process forced a complete revision of virus pattern chains handling. SK loop is now searched at level 4 of the process prior to tagging, in a direct processing of Virus pattern chains. Also, in the tagging process, all consequences of virus pattern chains are analyzed (formerly, there was some redundancy with the tagging process done out of all AC2 ). The virus pattern chaining is now a key process.
Vicinity analysis has been as well completely reshaped and extended to Exocet patterns scenario analysis.
Regarding Exocets patterns (at least for the forms already integrated in the process), The split of each super candidate in 2 scenario is now fully operational and again, the maximum has been done to improve the vicinity analysis.
Are missing now the last findings in the linked threads as:
1)Platinum Blonde Exocet specific pattern ,
2)Mini Row pattern found by ronk and Allan Barker,
3)And somehow some new ideas to extract from Ronk and Allan rank 0 SLGs offering a huge number of eliminations.
In that last case, may be the best way is to stick to Allan Barker model, That model is for the time being a kind of escape lane in my solver, mainly because the mix of both logics is not very easy. I will nevertheless study whether there is an equivalent process closer to the main logic in the tagging process;
Another problem to face is handling of huge lots of “hardest” puzzles.
I run thousands of puzzles mainly produced by coloin, but not only, to evaluate the difficulty as seen by the solver.
For the time being, I sort the results using the bloc-notes, which is not performing very well. I must organize the process to have a sorting capability if I want to be in a position to analyze a significant database.
Still a lot to do
champagne
- champagne
- 2017 Supporter
- Posts: 7878
- Joined: 02 August 2007
- Location: France Brittany
45 posts
• Page 3 of 3 • 1, 2, 3

