The New Sudoku Players' Forum

[eleven]

Guess some want easier puzzles and less discussions. One by Mike (m_b_metcalf ):

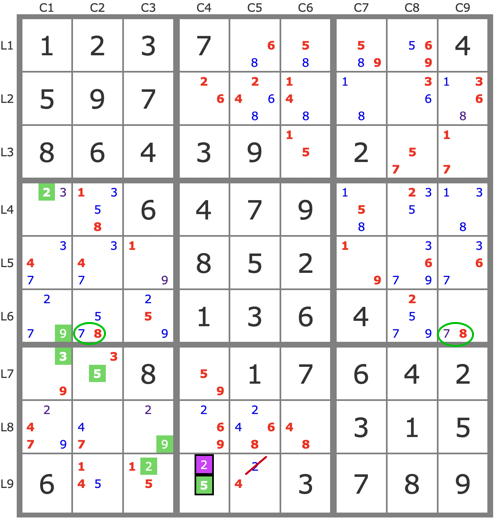
Code: Select all

 1 2 3 . . . . . 4
 5 . 7 . . . . . .
 8 6 4 3 . . 2 . .
 . . 6 4 7 9 . . .
 . . . 8 . 2 . . .
 . . . 1 3 6 4 . .
 . . 8 . . 7 6 4 2
 . . . . . . 3 . 5
 6 . . . . . 7 8 9

[RSW]

Guess some want easier puzzles and less discussions. One by Mike (m_b_metcalf )

Yes, thanks for the puzzle.

After basics:

Code: Select all

 +-----------------+--------------+-----------------+
 | 1     2     3   | 7   68   58  | 589  569   4    |
 | 5     9     7   | 26  2468 148 | 18   36    1368 |
 | 8     6     4   | 3   9    15  | 2    57    17   |
 +-----------------+--------------+-----------------+
 |c23    1358  6   | 4   7    9   |d158 d235  d138  |
 | 347   347  e19  | 8   5    2   |d19  d367  d367  |
 | 279   578   259 | 1   3    6   | 4    2579 d78   |
 +-----------------+--------------+-----------------+
 |b39    35    8   |a59  1    7   | 6    4     2    |
 | 2479  47    29  | 269 2468 48  | 3    1     5    |
 | 6    g15-4 f125 |a25 a24   3   | 7    8     9    |
 +-----------------+--------------+-----------------+


(4=259)b8p178 - (9=3)r7c1 - (3=2)r4c1 - (2=1356789)b6p1234569 - (9=1)r5c3 - (1)r9c3 = (1)r9c2 => -4r9c2; stte

[pjb]

Code: Select all

 1       2       3      | 7      6-8   a58     |i589    569    4     
 5       9       7      | 26     2468   148    | 18     36     1368   
 8       6       4      | 3      9     b15     | 2      57    c17     
------------------------+----------------------+---------------------
 23     f1358    6      | 4      7      9      |e158    235   e138   
 347     347    g19     | 8      5      2      |h19     367    367   
 279     578     259    | 1      3      6      | 4      2579  d78     
------------------------+----------------------+---------------------
 39      35      8      | 59     1      7      | 6      4      2     
 2479    47      29     | 269    2468   48     | 3      1      5     
 6       145     125    | 25     24     3      | 7      8      9     


(8=5*)r1c6 - (5=1)r3c6 - (1=7)r3c9 - (7=8)r6c9 - (8)r4c79 = (8-1)r4c2 = (1)r5c3 - (1=9)r5c7 - (9|5*=8)r1c7 => -8 r1c5; stte

Phil

[denis_berthier]

.

Code: Select all

Resolution state after Singles and whips[1]:
   +----------------+----------------+----------------+
   ! 1    2    3    ! 7    68   58   ! 589  569  4    !
   ! 5    9    7    ! 26   2468 148  ! 18   36   1368 !
   ! 8    6    4    ! 3    9    15   ! 2    57   17   !
   +----------------+----------------+----------------+
   ! 23   1358 6    ! 4    7    9    ! 158  235  138  !
   ! 3479 1347 19   ! 8    5    2    ! 19   3679 1367 !
   ! 279  578  259  ! 1    3    6    ! 4    2579 78   !
   +----------------+----------------+----------------+
   ! 39   35   8    ! 59   1    7    ! 6    4    2    !
   ! 2479 47   29   ! 269  2468 48   ! 3    1    5    !
   ! 6    145  125  ! 25   24   3    ! 7    8    9    !
   +----------------+----------------+----------------+
116 candidates

1) Simplest-first solution, in BC5:

Code: Select all

naked-pairs-in-a-row: r5{c3 c7}{n1 n9} ==> r5c9≠1, r5c8≠9, r5c2≠1, r5c1≠9
biv-chain[3]: r2c7{n8 n1} - r3c9{n1 n7} - r6c9{n7 n8} ==> r2c9≠8, r4c7≠8
biv-chain[3]: r4c1{n2 n3} - r7c1{n3 n9} - r8c3{n9 n2} ==> r6c3≠2, r8c1≠2
biv-chain[5]: r1c6{n5 n8} - r8c6{n8 n4} - r9n4{c5 c2} - c2n1{r9 r4} - r4c7{n1 n5} ==> r1c7≠5
hidden-single-in-a-column ==> r4c7=5
naked-pairs-in-a-row: r4{c1 c8}{n2 n3} ==> r4c9≠3, r4c2≠3
hidden-pairs-in-a-column: c9{n3 n6}{r2 r5} ==> r5c9≠7, r2c9≠1
naked-pairs-in-a-block: b3{r2c8 r2c9}{n3 n6} ==> r1c8≠6
stte

2) The two 1-step solutions in W6:

Code: Select all

whip[6]: r7c1{n3 n9} - r8n9{c3 c4} - c4n6{r8 r2} - c9n6{r2 r5} - r5n3{c9 c8} - r2c8{n3 .} ==> r4c1≠3
w1-tte

Code: Select all

whip[6]: r3c9{n7 n1} - r2n1{c9 c6} - c6n4{r2 r8} - r8c2{n4 n7} - c1n7{r8 r5} - c1n4{r5 .} ==> r6c9≠7
w1-tte

[yzfwsf]

Grouped AIC Type 2: (4=2)r9c5 - (2=5)r9c4 - r7c4 = (5-3)r7c2 = r7c1 - (3=2)r4c1 - r4c8 = (2-9)r6c8 = r6c13 - (9=1)r5c3 - r9c3 = 1r9c2 => r9c2<>4
stte

[P.O.]

Code: Select all

after singles and intersections:

1      2     3     7     68    58   a58+9 ga+56±9   4             
5      9     7     26    2468  148   18     36      1368           
8      6     4     3     9     15    2     f5+7    f1-7             
23    c+1358 6     4     7     9    c-158   235    c-138           
3479   1347  19    8     5     2    b+19    3679    1367           
279   d57+8  259   1     3     6     4      2579   e+78             
39     35    8     59    1     7     6      4       2             
2479   47    29    269   2468  48    3      1       5             
6      145   125   25    24    3     7      8       9             

r1n9{c8 c7} - r5c7{n9 n1} - r4n1{c7c9 c2} - c2n8{r4 r6} - r6c9{n8 n7} - r3n7{c9 c8} - b3n5{r3c8 r1c8} => r1c8 <> 6
ste.


[Mauriès Robert]

Hi all,
Here is my one-step solution with TDP after reducing the puzzle with the basic techniques.
P'(2r9c4) : (-2r9c4) => 5r9c4->5r7c2->[ ( 78r6c29 & 3r7c1->2r4c1 )->9r6c1->9r8c3 ]->2r9c3->... => -2r9c5 => r9c5=4, stte.

puzzle: Show

Robert

[StrmCkr]

als XY-Wing: A=r25c8{367}, B=r2345c8{23567}, C=b4p145{2347}, X,Y=7, 2, Z=6 => r1c8<>6

Code: Select all

als a) 2,3,4,7 @ 27,36,37
als b) 2,3,5,6,7 @ 16,25,34,43
als c) 3,6,7 @ 16 43
RC: 2,7  Z:3,6
  7,52,61,70,79 <>3, 6 

Code: Select all

+-------------------+----------------+------------------+
| 1      2      3   | 7    68    58  | 589  59-6   4    |
| 5      9      7   | 26   2468  148 | 18   (36)   1368 |
| 8      6      4   | 3    9     15  | 2    (57)   17   |
+-------------------+----------------+------------------+
| (23)   1358   6   | 4    7     9   | 158  (235)  138  |
| (347)  (347)  19  | 8    5     2   | 19   (367)  367  |
| 279    578    259 | 1    3     6   | 4    2579   78   |
+-------------------+----------------+------------------+
| 39     35     8   | 59   1     7   | 6    4      2    |
| 2479   47     29  | 269  2468  48  | 3    1      5    |
| 6      145    125 | 25   24    3   | 7    8      9    |
+-------------------+----------------+------------------+

singles to the end.

[jco]

After basics. For fun, using UR(36)r25c78

Code: Select all

.--------------------------------------------------------.
| 1     2     3   | 7    68    58  | 589  569    4       |
| 5     9     7   | 26   2468  148 | 18  c36#   c36(18)# |
| 8     6     4   | 3    9     15  | 2    57    d17      |
|-----------------+----------------+---------------------|
| 2-3   1358  6   | 4    7     9   | 158  235   d138     |
|a347  a347   19  | 8    5     2   | 19 cb36(7)# cb36(7)#|
| 279   578   259 | 1    3     6   | 4    2579  d78      |
|-----------------+----------------+---------------------|
| 39    35    8   | 59   1     7   | 6    4      2       |
| 2479  47    29  | 269  2468  48  | 3    1      5       |
| 6     145   125 | 25   24    3   | 7    8      9       |
'--------------------------------------------------------'

Code: Select all

                                        (1=783)r364c9
                                       /
(3=47)r5c12 - (7)r5c78 = UR = (1|8)r2c9                => -3 r4c1; ste
                                       \
                                        (8=713)r634c9

Thanks for the puzzle.
EDIT: Following Cenoman's suggestion (thanks!) for the writing of this move:
(3=47)r5c12 - (7)r5c78 = UR = (1|8)r2c9 - (187=3)r364c9 => -3 r4c1; ste

[Cenoman]

Guess some want easier puzzles and less discussions. One by Mike (m_b_metcalf ):

Good guess ! Thanks for the puzzle, eleven !

Code: Select all

 +----------------------+---------------------+----------------------+
 |  1      2      3     |  7     68    b58    |  589   569    4      |
 |  5      9      7     |  26    2468   148   |  18    36     1368   |
 |  8      6      4     |  3     9     a15    |  2     57    a17     |
 +----------------------+---------------------+----------------------+
 |  23     1358   6     |  4     7      9     |  158   235    138    |
 |  347   e347    19    |  8     5      2     |  19   f367   f367    |
 |  279    578    259   |  1     3      6     |  4     2579   8-7    |
 +----------------------+---------------------+----------------------+
 |  39     35     8     |  59    1      7     |  6     4      2      |
 |  2479  e47     29    |  269   2468  b48    |  3     1      5      |
 |  6     d145    125   |  25   c24     3     |  7     8      9      |
 +----------------------+---------------------+----------------------+

(7=15)r3c69 - (5=84)r18c6 - r9c5 = r9c2 - (4=73)r58c2 - (3=67)r5c89 => -7 r6c9; ste

Code: Select all

                                        (1=783)r364c9
                                       /
(3=47)r5c12 - (7)r5c78 = UR = (1|8)r2c9                => -3 r4c1; ste
                                       \
                                        (8=713)r634c9

Nice finding, JCO !
Just a writing suggestion:
(3=47)r5c12 - (7)r5c78 = UR = (1|8)r2c9 - (187=3)r364c9 => -3 r4c1; ste
The rule for writing ALS's is just a convention. In such cases, feel free to derogate...

[jco]

It seems that it would have been better to use externals instead of internals in the UR(36)r25c78 in my previous post:

(3)r4c9 = UR = (3)r5c12 => -3 r4c1; ste

@ Cenoman: thank you for your (very helpful) suggestion on the writing of that als part of my previous move.

[eleven]

Thanks to Mike and the solvers. One solution not posted is that.

Code: Select all

+--------------------+-------------------+-------------------+
| 1      2     3     | 7     68    58    | 589   569   4     |
| 5      9     7     | 26    2468  148   | 18    36    1368  |
| 8      6     4     | 3     9     15    | 2     57    17    |
+--------------------+-------------------+-------------------+
| 23     1358  6     | 4     7     9     | 158   235   138   |
| 347  ca347   19    | 8     5     2     | 19   b367  b367   |
| 279  c 578   259   | 1     3     6     | 4     2579 b78    |
+--------------------+-------------------+-------------------+
| 39   c 35    8     | 59    1     7     | 6     4     2     |
| 2479 ca47    29    | 269   2468  48    | 3     1     5     |
| 6      15-4  125   | 25    24    3     | 7     8     9     |
+--------------------+-------------------+-------------------+

(47=3)r58c2 - (3=8)b6p569 - (8=5734)r5678c2 => -4r9c2, stte

[denis_berthier]

One solution not posted is that.

Code: Select all

+--------------------+-------------------+-------------------+
| 1      2     3     | 7     68    58    | 589   569   4     |
| 5      9     7     | 26    2468  148   | 18    36    1368  |
| 8      6     4     | 3     9     15    | 2     57    17    |
+--------------------+-------------------+-------------------+
| 23     1358  6     | 4     7     9     | 158   235   138   |
| 347  ca347   19    | 8     5     2     | 19   b367  b367   |
| 279  c 578   259   | 1     3     6     | 4     2579 b78    |
+--------------------+-------------------+-------------------+
| 39   c 35    8     | 59    1     7     | 6     4     2     |
| 2479 ca47    29    | 269   2468  48    | 3     1     5     |
| 6      15-4  125   | 25    24    3     | 7     8     9     |
+--------------------+-------------------+-------------------+

(47=3)r58c2 - (3=8)b6p569 - (8=5734)r5678c2 => -4r9c2, stte

Counted according to my method, this chain has length 9 (2+3+4).
I found the same elimination, with a whip of length 7:
whip[7]: r9n1{c2 c3} - r5c3{n1 n9} - r6n9{c3 c8} - c8n2{r6 r4} - r4c1{n2 n3} - c2n3{r5 r7} - b7n5{r7c2 .} ==> r9c2≠4
but I didn't report it, because I had still shorter ones (length 6).
Note I'm not saying that your chain and mine are the same. They are just doing the same elimination.

[eleven]

When i look at your

whip[6]: r7c1{n3 n9} - r8n9{c3 c4} - c4n6{r8 r2} - c9n6{r2 r5} - r5n3{c9 c8} - r2c8{n3 .} ==> r4c1≠3

i don't see the link r8n9{c3 c4}, cause there is a 9 in r8c1. When i replace it by c4n9{r7 r8} it would work for my understanding of your chains.
Then the chain uses 9 cells, 5 strong and 5 weak links. Additionally you need the hidden memory links 3r4c1-r5c12 and 6r2c4-r2c8.
My solution needs 7 cells, 3 strong and 2 weak links - and nothing hidden. So mine is much shorter

[denis_berthier]

When i look at your

whip[6]: r7c1{n3 n9} - r8n9{c3 c4} - c4n6{r8 r2} - c9n6{r2 r5} - r5n3{c9 c8} - r2c8{n3 .} ==> r4c1≠3

i don't see the link r8n9{c3 c4}, cause there is a 9 in r8c1.

You don't see the link because it is not a link but a CSP-Variable and its values content. In r8n9 (not in r8c1), the c1 (not the 9), i.e. n9r8c1, is t-candidate, linked to the previous right-linking one (n9r7c1).

When i replace it by c4n9{r7 r8} it would work for my understanding of your chains.

It works also with that way.

Then the chain uses 9 cells, 5 strong and 5 weak links. Additionally you need the hidden memory links 3r4c1-r5c12 and 6r2c4-r2c8.

There are neither strong nor weak links, let alone hidden ones. There are only csp-variables and links. There's no pure logic way of defining a rating based on the number of links (which amounts to counting the number of inferences in the mesozoic view of chains as networks of inferences).

My solution needs 7 cells, 3 strong and 2 weak links - and nothing hidden.

Nothing hidden? How do you count all the hidden "strong" and "weak" links inside the Subsets? If you count them, you have to add 2+3+4=9 "strong" links plus as many "weak" ones (and that is counting only 1 link for each base or cover set).