The New Sudoku Players' Forum

[Jeff]

I got this puzzle from Max and found that it is a good exercise for application of xyz-wing and xy-chain. The solution will be posted later. Other solutions are also welcome.

[stuartn]

Jeff - could you post it in a form that can be cut and pasted please?

Stuartn

http://www.brightonandhove.org/Sudolinks.htm

[Jeff]

Here is the cut and paste format.

{27} {3} {6} | {5} {4} {9} | {8} {1} {27}
{1} {258} {58} | {7} {6} {38} | {4} {9} {235}
{4} {578} {9} | {2} {1} {38} | {367} {56} {357}

{8} {4} {3} | {9} {7} {5} | {1} {2} {6}
{9} {1} {2} | {6} {3} {4} | {5} {7} {8}
{6} {57} {57} | {8} {2} {1} | {9} {3} {4}

{23} {28} {48} | {1} {5} {7} | {236} {46} {9}
{257} {9} {457} | {3} {8} {6} | {27} {45} {1}
{357} {6} {1} |{4} {9} {2} | {37} {8} {357}

[Scott H]

I don't know any solvers that can paste the preceding candidate format. Does anyone?

Here's the puzzle in a standard pasteable format:

Code: Select all

.36|549|81.
1..|76.|49.
4.9|21.|...
---+---+---
843|975|126
912|634|578
6..|821|934
---+---+---
...|157|..9
.9.|386|..1
.61|492|.8.

[stuartn]

I don't know any solvers that can paste the preceding candidate format. Does anyone?

Yes - this one for Excel can. - and it'll export in candidate format. You just 'paste special' it as text at K1 on sheet2 and hit the button.

http://www.brightonandhove.org/Sudolinks.htm

stuartn

[tso]

1) The only cells in column 1 that can be 5 are in box 7, so remove the cadidate '5' from r8c3.

2)
r7c2=8 => r3c2<>8
r7c2=2 => r2c2<>2, forming a naked pair r2c3 [58][58] => r3c2<>8
therefore, r3c2<>8

2b) r3c6 is now the only cell in row 3 that can be 8.
2c) r2c6 is now the only cell in row 2 that can be 3. (remove candidate 3 from r2c9.)

3) Naked Pair r3c2-r6c2 [57][57]
therefore, r2c2 <> 5

At this point, I can connect cells to form BINARY GROUPS with or without labeling the 'edges'.

The interesting thing here is that this is easier with pencil and paper than with a computer or solver. Making these drawings for this post took far longer than the 10 minutes it took to find these solutions on paper.




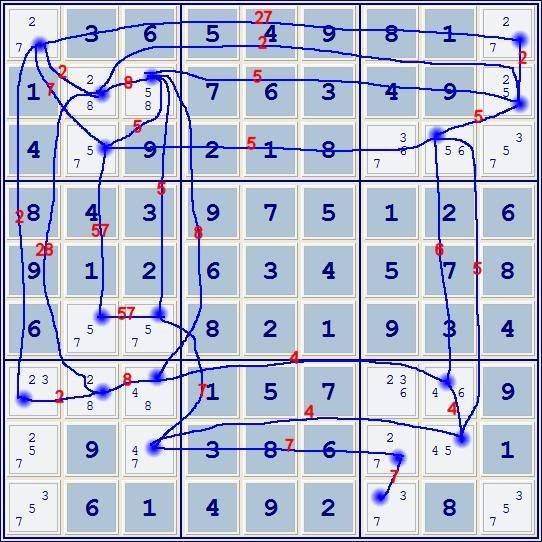
This first image has all 2-candidate cells connected by labeled edges, the labels being the candidates both share. A 'nice' loop that has two and ONLY two edges in sequence with the same label will form a proof.



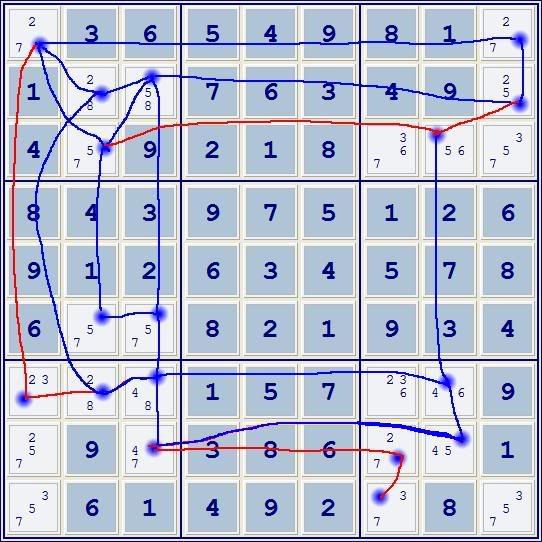
This second image is a somewhat simpler drawing, some of the lines within triples and quads being assumed. (For example, r2678c3 is connect with a single straight line for clarity.) The BLUE lines connecting the cells are a BINARY GROUP. All cells within this group, taken together, can exist in exactly two states without contradiction along the blue lines. Proofs must include at least one RED line.


Using red line r2c9-r3c8:

r3c8=6 => r7c8=4 => r7c3=8 => r2c3=5 => r2c9=2
r2c8=5 => r2c9=2
Therefore, r2c9=2
The rest is elementary.


Using red line r3c28:

r3c8=6 => r7c8=4 => r7c3=8 => r2c3=5 => r3c2=7
r2c8=5 => r3c2=7
Therefore, r3c2=7
The rest is elementary.


No 'nice' loop using the red line r1c1-r7c3 can be made without also using one of the other two red lines.
For example,

r1c9=7 => r1c1=2 => r7c1=3
r1c9=2 => r2c9=5 => r3c8=6 => r7c8=4 => r7c3=8
=> r7c2=2 => r7c1=3
Therefore, r7c1=3

Then:
r8c8=5 => r8c1<>5
r8c8=4 => r8c3=7 => r9c1=5 => r8c1<>5
Therefore, r8c1<>5.
The rest is elementary.


I haven't stated it explicitly before, but a BINARY GROUP isn't really a group of CELLS, it's a group of CONNECTIONS between the candidates of the cells -- the EDGES.

I don't know what to call this last situation. r1c1-r7c3 cannot be changed from red to blue -- if it was, the BINARY GROUP would have THREE states instead of the required TWO. But if WAS considered blue, it wouldn't cause the method to fail. I suppose a different name could be used instead of BINARY GROUP, like INTERNALLY CONSISTANT GROUP or ICG for short. I dunno yet. Open to suggestions.

Which of these slightly different methods is easier probably depends on the specific problem and what sort of tools you are using, size of print-out, etc. You don't have to label all the edges, just enough to find a proof.

[Scott H]

tso, I solved your step 2(a) with "xyz-wing" 62-32-23, excluding 5 from r2c2. Then a 2,8 naked pair in column 2 excludes 8 from r3c2. The reasoning from 5,8 @ r2c3 in the xyz-wing is almost identical to your reasoning from 2,8 @ r7c2. I then found xy-chains excluding candidates even without noticing the unique choices in column 6

I suggest you consider internal group consistency to be the defining criterion for your edges being blue instead of red. My view of a red edge is it's potentially weak. If you have a red edge that's already strong, you can color it blue and extend any consistent groups it touches or connects. The "binary groups" you start with are just one of several criteria that establish an internally consistent group.

It doesn't hurt to color some strong edges as red -- the analysis still works -- but coloring strong edges blue as soon as possible simplifies the search for useful loops.

[Wolfgang]

Cannot find an interesting solution (one you could see faster than solving it with a guess). My shortest chain uses the noname pattern:
r7c8=6,r7c3=4,r7c2=8,r2c3=8,r2c2=2,r1c1=7,r3c2=5 -
not possible, because r3c8={5,6}
=> r7c8=4

Edit: ok, with tso's 2) and 3) it would become "acceptable":
r7c8=6,r7c3=4,r2c3=8,r3c2=5

[Jeff]

Interesting grid indeed. Here is my solution.

Locked to column => r8c3<>5

xy-chain:
Starting r7c2, 28-84-47-72 => r7c7<>2 and r8c1<>2 => r8c7=2
Unfortunately, this does not lead to a solution.

xyz-wing (refer left diagram):
28-258-58 => r3c2<>8 => r3c6=8 => r2c6=3 => r2c9<>3

Naked pair in column 2 => r2c2<>5

xy-chains: I have identified 22 xy-chains, but the one posted by Tso is the shortest (refer right diagram)

Starting r3c8, 56-64-48-85 => r2c9<>5 and r3c2<>5
Starting r3c8, 56-64-48-82-28-85 => r2c9<>5 and r3c2<>5

Starting r1c1, 27-75-58-84-46-65-52 => r1c9<>2 and r2c2<>2
Starting r1c1, 27-75-57-75-58-84-46-65-52 => r1c9<>2 and r2c2<>2

Starting r1c1, 27-75-56-64-48-82-28-85-52 => r1c9<>2
Starting r1c1, 27-75-58-82-28-84-46-65-52 => r1c9<>2
Starting r1c1, 27-75-57-75-58-82-28-84-46-65-52 => r1c9<>2

Starting r1c1, 27-75-56-64-48-82 => r7c1<>2 and r2c2<>2
Starting r1c1, 27-72-25-56-64-48-82 => r7c1<>2 and r2c2<>2

Starting r1c1, 27-75-58-84-46-65-52-28-82 => r7c1<>2
Starting r1c1, 27-75-57-75-58-82-25-56-64-48-82 => r7c1<>2
Starting r1c1, 27-75-57-75-58-82-25-56-64-48-82 => r7c1<>2

Starting r8c8, 54-47-75-58-82-25 => r3c8<>5 and r9c9<>5
Starting r8c8, 54-47-75-57-75-58-82-25 => r3c8<>5 and r9c9<>5

Starting r8c8, 54-47-75-57-75 => r3c8<>5

Starting r2c2, 82-25-56-64-48 => r2c3<>8 and r7c2<>8

Starting r6c3, 75-58-84-46-65-57 => r6c2<>7

Starting r2c3, 58-84-46-65-57-75 => r6c3<>7
Starting r2c3, 58-82-28-84-46-65-57-75 => r6c3<>7

Starting r8c3, 47-75-57-75-56-64 => r7c3<>4 and r8c8<>4
Starting r8c3, 47-75-58-82-25-56-64 => r7c3<>4 and r8c8<>4
Starting r8c3, 47-75-57-75-58-82-25-56-64 => r7c3<>4 and r8c8<>4

Did you find the xyz-wing and does your xy-chains appear in the above list? Let me know if I have missed out any of them.

[Jeff]

Can an xy-chain testing program be written to find out the total number of xy-chains in a grid.

[Wolfgang]

xyz-wing (refer left diagram):
28-258-58 => r3c2<>5 => r3c6=8 => r2c6=3 => r2c9<>3

Suppose you mean
28-258-58 => r3c2<> 8 => r3c6=8 => r2c6=3 => r2c9<>3

Fine, how many ways there are to solve it

[Jeff]

Yes, post edited. Thanks

[Jeff]

Fine, how many ways there are to solve it

Each of the 22 xy-chains should complete the puzzle.

[Scott H]

Can an xy-chain testing program be written to find out the total number of xy-chains in a grid.

Of course! See Nonrepetitive Paths and Cycles in Graphs with Application to Sudoku by David Eppstein.

Searching in a more brute force manner than Eppstein's algorithms also works.

[Jeff]

Great paper, thanks Scott.