I would name this 'Arrow Sudoku' but that's already a well-known variant (this is starting to feel like trying to choose a good unused name for a Pokemon game
It starts from a pretty straightforward idea. We have a grid full of arrows so we have to move through the grid following them to find the longest possible path.
The path ends when we enter an infinite loop or we get out of the grid (it could loop to the other side like a toroid but I'm not considering that case)
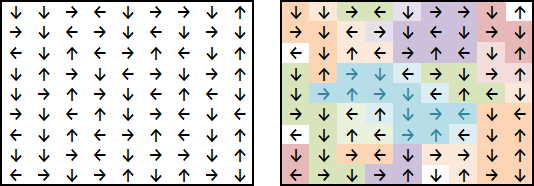
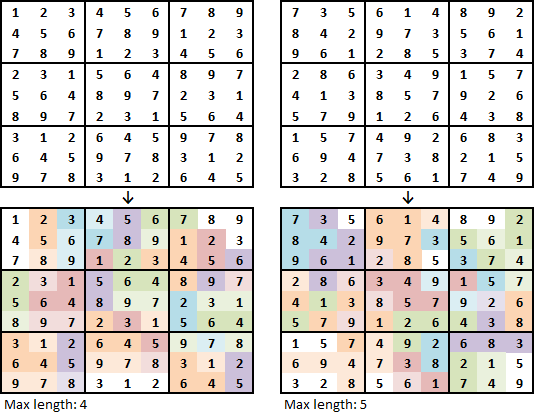
In this example the longest path (blue) has 11 squares.
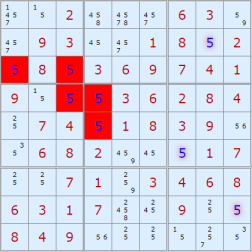
From there we could try a little challenge: Find the perfect square (arrows non-repeated in any row/column) with the longest path:
I'm thinking at least 1 clue should be given since a completely empty puzzle would have (at least) 4 solutions because of rotation.
There are many combinations there so it's already a challenging question but probably you are already guessing where I'm going with this.
Diagonal arrows can also be included, and I implemented a dot which would be a dead end of the path, so with that we have a complete Numpad we can translate to numbers 1-9.
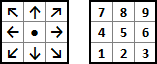
And from there the question is: From all possible completed sudoku grids (without considering rotation), which one has the longest path?
Examples: Show