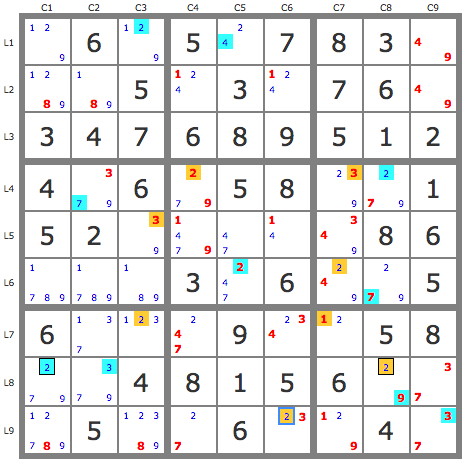
Hi totuan and Robert,
totuan wrote:My path for this one - an almost coloring 2’s (kite or others name – I’m not sure

).
Nice move! Not that it matters one bit, but if you're interested, I'd call it Almost X-Chain (or Almost Finned Swordfish with fish notation). "Almost Coloring" is not incorrect, but it's not very specific as it could mean anything (Simple Coloring, Multi-Coloring, X-Coloring, 3D Medusa, GEM, Full Tagging...). In this case Simple Coloring would not work (not all conjugate links), so you'd need at least Multi-Coloring or X-Coloring.
Mauriès Robert wrote:I have more trouble understanding Totuan's one.
Let me try to explain. It's a nice example of using a nested AIC (in this case an X-Chain) as a node within an AIC. Below I've changed the colors for demonstration purposes:
totuan wrote:(2)r7c3=(2-7)r8c1=r6c1-r4c2=r4c8-{almost coloring 2’s: (2)r4c8=[(2)r7c3=r1c3-r1c5=r6c5-r6c8=r8c8]} => r7c7<>2, stte
If it weren't for the spoiler
2r4c8 we'd have an
X-Chain with end points 2r7c3 and 2r8c8, which would eliminate 2r7c7 (and 2r8c1). In other words it's an Almost X-Chain with the strong link: [X-Chain]=2r4c8. To make it eliminate something both sides must prove the same eliminations, as usual. The
green part does it for the spoiler side. It's perhaps a bit clearer if reversed:
[(2)r7c3 = r1c3 - r1c5 = r6c5 - r6c8 = (2)r8c8] = (2-7)r4c8 = r4c2 - r6c1 = (7-2)r8c1 = (2)r7c3 => -2 r7c7,r8c1; stte
Note that the nested
X-Chain as a whole is the first node of the outer AIC. The second node is the strongly linked spoiler
2r4c8. One or the other must be true. Without the [brackets] we'd have a violation of AIC rules because of two adjacent strong links (=). Now we don't because the bracketed part is a single boolean node (true or false), despite being an AIC internally.
As a matrix (the first three rows forming the Almost X-Chain):
- Code: Select all
2r7c3 2r1c3
2r1c5 2r6c5
2r8c8 2r6c8 2r4c8
7r4c8 7r4c2
7r6c1 7r8c1
2r7c3 2r8c1
------------------------------------
-2r7c7,
-2r8c1
Note that the end-points also get -2 r8c1. In fact, we could shorten the chain to get just that:
[(2)r7c3 = r1c3 - r1c5 = r6c5 - r6c8 = (2)r8c8] = (2-7)r4c8 = r4c2 - r6c1 = (7)r8c1 => -2 r8c1; stte
Or if one likes it really short, it could be written as an Almost Finned Swordfish:
(2)C358\r16[r8b7] = (2-7)r4c8 = r4c2 - r6c1 = (7)r8c1 => -2 r8c1; stte
- Code: Select all
2r7c3 2r1c3
2r1c5 2r6c5
2r8c8 2r6c8 2r4c8
7r4c8 7r4c2
7r8c1 7r6c1
------------------------------
-2r8c1
From the matrix it's easy to see that it could also be written as a Kraken Column (2C8):
(2-7)r4c8 = r4c2 - r6c1 = (7)r8c1||(2)r6c8 - r6c5 = r1c5 - r1c3 = (2)r7c3
||
(2)r8c8And from that it's easy to see that there are two other ways to split it as an Almost-AIC:
[(2)r7c3 = r1c3 - r1c5 = r6c5 - r6c8 = (2-7)r4c8 = r4c2 - r6c1 = (7)r8c1] = (2)r8c8 => -2 r8c1
[(2)r8c8 = (2-7)r4c8 = r4c2 - r6c1 = (7)r8c1] = (2)r6c8 - r6c5 = r1c5 - r1c3 = (2)r7c3 => -2 r8c1
The latter could be called Almost L2-Wing.
Hope this helped to get an idea how Almost-AICs work. Note that an Almost-AIC is the strongly linked combo
[AIC]=Spoiler, i.e. the pattern that exists in the grid. The complete outer chain that contains an Almost-AIC is still an AIC. Similarly the nested
[AIC] node is an actual AIC (within the context of the outer chain, not in the grid). Of course, if the pattern works without any further chaining, like with the spoiler 2r8c8 above, then it's both an Almost-AIC and an AIC (kind of like a finned fish where the fin sees the elimination directly).