The New Sudoku Players' Forum

by **ArkieTech** » Sat Dec 14, 2019 6:04 am

Code: Select all: *-----------* |7..|...|..6| |..4|8.9|3..| |..9|.2.|4..| |---+---+---| |5..|1.4|..3| |...|265|...| |9..|7.8|..4| |---+---+---| |..8|.4.|1..| |..1|5.6|8..| |2..|...|..7| *-----------* 7.......6..48.93....9.2.4..5..1.4..3...265...9..7.8..4..8.4.1....15.68..2.......7

Play/Print this puzzle online

by **SpAce** » Sat Dec 14, 2019 8:24 am

Code: Select all: .-------------------.-----------.---------------------------. | 7 ^125'8 25 | 4 15 3 | ^5(9)'2* ^12589* 6 | | 16 ^156'2 4 | 8 15 9 | 3 7 ^125* | | 138 1358 9 | 6 2 7 | 4 158 158 | :-------------------+-----------+---------------------------: | 5 ^28'6 267 | 1 9 4 | ^26'7 268 3 | | 1348 1348 37 | 2 6 5 | ^7{9} 189 189 | | 9 126 26 | 7 3 8 | 256 1256 4 | :-------------------+-----------+---------------------------: | 36 7 8 | 39 4 2 | 1 3569 59 | | 34 349 1 | 5 7 6 | 8 2349 2[9]* | | 2 34569 356 | 39 8 1 | 6-9 3469 7 | '-------------------'-----------'---------------------------'

Almost M2-Wing (*)

Code: Select all: [(9=2)r8c9 - r2c9 = (2-9)r1c8 = (9)r1c7] ** || || ------------------------------------- (2)r4c7 ||/ || (2-9)r1c7 = (9-8)r1c8 = r1c2 - (8)r4c2 || \ || (7)r4c7 - (7=9)r5c7 * (2)r2c9 = r2c2 ------------ (2)r4c2 || || || (6)r4c2 -- (6)r4c7 => -9 r9c7; stte

9x9 TM: Show

as a triple kraken: Show

as an AIC: Show

Btw, here's a (Hodoku-assisted) variant of the same theme as a single kraken:

Code: Select all: 2c2 [##] 2c7 [2c8] 2c9 .--------------------.------------.---------------------. | 7 *1258 A#25 | 4 15 3 | *259 C*12589 6 | 2R1 | 16 *1256 4 | 8 15 9 | 3 7 *125 | 2R2 | 138 1358 9 | 6 2 7 | 4 158 158 | :--------------------+------------+---------------------: | 5 *268 B#267 | 1 9 4 | *267 D*268 3 | 2R4 | 1348 1348 37 | 2 6 5 | 79 189 189 | | 9 126 26 | 7 3 8 | 256 1256 4 | :--------------------+------------+---------------------: | 36 7 8 | 39 4 2 | 1 3569 59 | | 34 349 1 | 5 7 6 | 8 E*2349 *29 | 2R8 | 2 34569 356 | 39 8 1 | 6-9 3469 7 | '--------------------'------------'---------------------'

Kraken Finned Jellyfish: (2)R1248\c2789 f:r14c3 => [2r14c3 == 2r148c8]

Code: Select all: A#(2)r1c3 - r2c2 = r2c9 - (2=9)r8c9 || B#(2-7)r4c3 = r4c7 - (7=9)r5c7 || C*(2-9)r1c8 = (9)r1c7 || D*(2-8)r4c8 = r4c2 - r1c2 = (8-9)r1c8 = (9)r1c7 || E*(2)r8c8 - (2=9)r8c9 => -9 r9c7; stte

8x8 TM: Show

The logic is that if the fins are false the fish is true, as usual, but it also implies that every cover sector must have a true base candidate (Rank 0). Thus any of the cover sets has a personal strong link with the fins and can be used individually as part of a kraken. In this case column 8 works best. Note that 2r6c8 is excluded because it's not a base candidate (otherwise we'd just use the kraken column, of course, but it would be more difficult here).

I explained the logic just in case, because this type of kraken fish usage is not commonly seen here. I doubt it's in the range of most manual players anyway, but it could be useful if the full fish body doesn't have applicable weak links. Another example (totally found by Hodoku) below.

2nd kraken fish sample: Show

--
Edit. Added AIC and Kraken Fishes.

by **Mauriès Robert** » Sat Dec 14, 2019 11:30 am

Hi,
Resolution with TDP starting (as SpAce) from pair 29r8c9.
P(9r8c9) = {9r8c9, 9r1c7,...}
P(2r8c9) = {2r8c9, 29r1c78, 8r1c2, 2r2c2, 6r4c2, 2r6c3, 8r4c8, 2r4c7, 2r1c8, 9r1c7,...}
=> r1c7=9, stte.
(see diagram and puzzle below)

Code: Select all: 9r8c9 -> 9r1c7 And, > 8r4c8 - - - - - - > 2r4c7- -> / / | > 8r1c1 / | / \ / | / > 6r4c2 -> 2r6c3 | 2r8c9 -> 29r1c7 / | \ / | > 2r2c2 | \ | >- - - - - - - - - - - - - - - - - > 2r1c8 -> 9r1c7

puzzle: Show

Robert

by **SpAce** » Sat Dec 14, 2019 12:10 pm

Hi Robert,

Thanks for the diagram! Much easier to follow with that!

by **Mauriès Robert** » Sat Dec 14, 2019 12:46 pm

Hi SpAce,

SpAce wrote:Thanks for the diagram! Much easier to follow with that!

Yes, after your remark on linear chains and complex chains (nets), I understood that it would be useful to use diagrams to better explain the construction of a track.

Here is also, another way to solve the puzzle with an anti-track and Th 2 TDP part 1.

Code: Select all: P'(9r9c2) <=> -9r9c2 -> 2r8c9 -> diagram below > 8r4c8 - - - - - - > 2r4c7- -> / / | > 8r1c1 / | / \ / | / > 6r4c2 -> 2r6c3 | 2r8c9 -> 29r1c7 / | \ / | > 2r2c2 | \ | >- - - - - - - - - - - - - - - - - > 2r1c8 -> 9r1c7 => -9r9c7, stte.

Robert

by **eleven** » Sat Dec 14, 2019 7:59 pm

Code: Select all: *--------------------------------------------------------------* | 7 b1258 b25 | 4 b15 3 | h259 h12589 6 | | 16 b1256 4 | 8 15 9 | 3 7 a125 | | 138 1358 9 | 6 2 7 | 4 158 158 | |-----------------------+---------------+----------------------| | 5 c268 d267 | 1 9 4 | f267 268 3 | | 1348 1348 37 | 2 6 5 | 79 189 189 | | 9 126 d26 | 7 3 8 | g256 1256 4 | |-----------------------+---------------+----------------------| | 36 7 8 | 39 4 2 | 1 3569 59 | | 34 349 1 | 5 7 6 | 8 2349 29 | | 2 34569 e356 | 39 8 1 | f69 3469 7 | *--------------------------------------------------------------*

2r2c = 2518r2c1,r1c352 - (2|8 = *6)r4c2 - r46c3 = r9c3 - *6r49c7 = (6-5)r6c7 = 59r1c78 => -2r1c78, stte

by **SpAce** » Sat Dec 14, 2019 11:51 pm

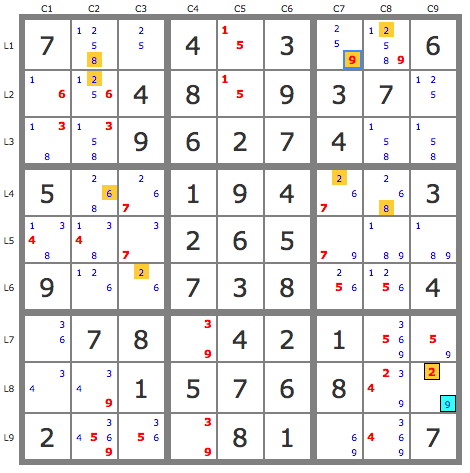
eleven wrote: 2r2c = 2518r2c1,r1c352 - (2|8 = *6)r4c2 - r46c3 = r9c3 - *6r49c7 = (6-5)r6c7 = 59r1c78 => -2r1c78, stte

Very nice. Again you need the comma, though:

2r2c9 = (2,518)r2c2,r1c352 - (2|8=6*)r4c2 ...

...or explicitly (2nd node: r1c78 used to avoid repetition, could be r2c2 too):

2r2c9 = r1c78 - r1c23 = 2r2c2 & 518r1c352 - (2|8=6*)r4c2 ...

Otherwise the following weak link doesn't work properly because 2r1c3 doesn't see 2r4c2. Same thing as yesterday.

--
Btw, some would prefer this but I don't particularly like it:

2r2c9 = 2r2c2 & 518r1c352 - (2|8=6*)r4c2 ...

Its problem is that 518r1c352 is not directly strongly-linked with 2r2c9 but dependent on 2r2c2. The comma is better because it implies such internal interactions within the node while '&' doesn't. (It's not incorrect, though. It just skips part of the logic flow.)

by **rjamil** » Thu Dec 19, 2019 4:04 pm

Code: Select all: +-------------------+-----------------------+-------------------------+ | 2357 1247 12345 | 24569 8 23459 | 345679 13479 1345679 | | 358 (48) 9 | 7 356-4 1 | 2 34 3456 | | 2357 6 12345 | 2459 2345 23459 | 34579 8 134579 | +-------------------+-----------------------+-------------------------+ | 1 9-4 456 | 4589 (45) 45789 | 3678 37 2 | | 69 3 246 | 12489 124 24789 | 678 5 67 | | 258 (28) 7 | 3 (25) 6 | 1 49 49 | +-------------------+-----------------------+-------------------------+ | 237 5 1238 | 1248 9 2348 | 347 6 1347 | | 4 129 1236 | 1256 7 235 | 359 1239 8 | | 69 1279 12368 | 124568 123456 23458 | 34579 123479 134579 | +-------------------+-----------------------+-------------------------+

Almost Locked Set move: 2458 @ r26c2 r46c5 => -4 @ r4c2 r2c5; stte

R. Jamil

The New Sudoku Players' Forum

December 14, 2019

December 14, 2019

Re: December 14, 2019

Re: December 14, 2019

Re: December 14, 2019

Re: December 14, 2019

Re: December 14, 2019

Re: December 14, 2019

Re: December 14, 2019