The New Sudoku Players' Forum

[goldie5218]

hi guys , can someone help me please? ive advanced thru the ranks in sudoku (generally ok up to very hard) but now want to tackle coloring!
apologies in advance to the authors of all the explanation notes on colouring but they are 'reeeealy' confusing to a beginner. first of all lets take the terms themselves, simple/super/multi etc etc and yet Sadman states that all but 'simple' colouring is beyond most humans!!! all im trying to do is solve the simple suduko colors1/2/3 . ss etc on the Simple Suduko web site. i love these puzzles and want to improve my solving skills. now i understand the principle of using colour to distinquish between cells that can hold a true vs a false version of a particular candidate (and at this stage i admit we dont know which is which - and use the colouring technique to identify the "true" version) my point is that no one seems to be able to spell out - in plain idiot language - just how the diff colours are applied. ok we have been told that the choice of a particular colour is strictly arbitrarily ie. use what we like. but the key point seems has been completely overlooked, just where do you start with your choosen colour if there are three candidates in a row/col/block? sure the 'hints' tell you what cells hold the 'false' values but what i want to know is just how did you arrive at those particular cells amongst the many cells available? as an example, in the puzzle "colors1.ss" from the Simple Suduko page there are a total of 18 (5) candidates yet only a single candidate is able to be erased as a result of using the colouring method?. and just to test my understanding i would have erased that particular candidate (without the use of colouring) simply because there are another two candidates in the same block which are also occupying the same column. ie blocked candidates, so please, please,please can someone walk me thru the correct use of the colouring technique in 'layperson's language ? cheers goldie

[tso]

Here's the the coloring example from colors1.ss filtered so all we see are the cells that might still contain a '5':

Code: Select all

  .   .   .  |  5   5   .  |  .   .   . 
  .   .   .  |  .   .   .  |  .   .   . 
  .   .   .  |  .   .   .  |  .   .   . 
-------------+-------------+------------
  5   .   .  |  5   5   .  |  .   .   5 
  5   5   .  |  .   5   .  |  .   5   . 
  .   .   .  |  5   5   .  |  .   .   5 
-------------+-------------+------------
  .   .   .  |  .   .   .  |  .   .   . 
  .   5   .  |  .   .   .  |  .   .   5 
  5   5   .  |  .   .   .  |  .   5   . 


To apply coloring, start with ANY 5 that is part of a CONJUGATE PAIR. You have a conjugate pair when there are exactly two 5s in the same group (row, column, box). Exactly one of the two must be "true", that is, a 5.

Lets start with the first one -- row 1, column 4. We'll color or label that one with a plus sign. The 5 in row 1, column 5 is the only other 5 in the same box as the first -- so we label it OPPOSITE the first one, in this case, a minus sign. Here's the situation:

Code: Select all

  .   .   .  | +5  -5   .  |  .   .   . 
  .   .   .  |  .   .   .  |  .   .   . 
  .   .   .  |  .   .   .  |  .   .   . 
-------------+-------------+------------
  5   .   .  |  5   5   .  |  .   .   5 
  5   5   .  |  .   5   .  |  .   5   . 
  .   .   .  |  5   5   .  |  .   .   5 
-------------+-------------+------------
  .   .   .  |  .   .   .  |  .   .   . 
  .   5   .  |  .   .   .  |  .   .   5 
  5   5   .  |  .   .   .  |  .   5   . 

Unfortuanately, there are no other conjugate pairs connected to these two cells. Column 4 and 5 both have more than two 5s. We cannot make any inferences from this, so we erase the colors/labels and start again.

Reading line by line like a book, the very next 5 we come across that is part of at least one conjugate pair is row 5, column 8. Label it PLUS. (Or you could use MINUS, or BLUE -- it doesn't matter.)

Row 9, column 8 (r9c8) is a conjugate pair with the r5c8, so it is labeled opposite the first, that is MINUS.

R8c9 and r9c8 are a conjugate pair, so r8c9 is labled PLUS.

R8c2 and r8c9are a conjugate pair, so r8c2 is labled MINUS.

There are no more conjugate pairs connected to these four cells. Each pair is labeled opposite each other. The situation looks like this:

Code: Select all

  .   .   .  |  5   5   .  |  .   .   . 
  .   .   .  |  .   .   .  |  .   .   . 
  .   .   .  |  .   .   .  |  .   .   . 
-------------+-------------+------------
  5   .   .  |  5   5   .  |  .   .   5 
  5  [5]  .  |  .   5   .  |  .  +5   . 
  .   .   .  |  5   5   .  |  .   .   5 
-------------+-------------+------------
  .   .   .  |  .   .   .  |  .   .   . 
  .  -5   .  |  .   .   .  |  .   .  +5 
  5   5   .  |  .   .   .  |  .  -5   . 



IMPORTANT -- we can NOT tell if the PLUSES are the ones that contain 5s or the MINUSES do -- all we know is that EITHER all the cells labeled plus are 5, OR all the cells labeled minus are 5.

Look at r5c2 -- it is in the same row as a PLUS and the same column as a MINUS. Either the PLUS is a 5 or the minus is a 5 -- either way, r5c2 is NOT a five.

It wouldn't matter what two labels or colors you used, nor which cell you start from. As long as you label all conjugate cells that opposite you will get the same result.

Notice that the two cells at the top, r1c4 and r1c5 are not labeled in the final solution as neither is part of a conjugate pair with the other four cells -- only each other. When applying simply coloring, all the cells colored WILL BE IN A SINGLE CONNECTED GROUP. Multiple coloring will involve two or more separate groups, each of which will use a pair of colors.

[Lummox JR]

Regular coloring actually allows multiple conjugate pairs; it just happens that in this case that doesn't help. Using just one pair is just a crippled form of the technique. As I've brought up elsewhere, in common parlance the consensus seems to be that simple coloring is merely limited to one digit, not one conjugate pair.

[goldie5218]

hi tso,hi lummox JR, first of all a big thank you for trying to help - secondly, i did warn you that i find complicated instructions difficult to grasp. lummox JR your comments really flummoxed me! i have no idea what you are even talking about, my problem was with simple colouring where does the 'regular' colouring come into this, and are you saying that 'simple' colouring is only of use if you have single candidates? please clarify as im even more confused than before. tso, i follow the main theme of your explanation, and grasp the method of colouring the diff candidates in each pair, where you lose me is in the reasoning as to how to identify which candidates you are allowed to erase as a result of this method. in the sample puzzle there are three candidates (5) in the block that the single 'erasable' candidate is in, and because of this i cannot understand why that single candidate is selected for erasure. also please bear with me but if i start from the beginning, and tackle each row first, i find a pair of 5's on r8,then i find a pair in col 8 and a pair in blocks 2 and 9. i understand that the pair in block two are not linked to other pairs so can be discarded as regards the colouring method, but i just dont seem to grasp how the alternate colouring leads to the erasure of the single candidate in block four. i seem to feel that im doing something wrong with the colouring.you say that that particular candidate only can be erased because it is linked to two diff colours? but i see other candidates (5) in the same block, on the same row, and in the same column! so my (dumb)question is, why that particular candidate? oh and just for fun i tried to tackle the puzzle colors 2.ss. there you may erase six candidates (9) out of a total of 11. talk about colour confusion! if i cant manage a single candidate i accept i am in serious need of serious help before tackling the more complex puzzles - but honestly guys, reading up on colours on the forum and linked sites only seems to confuse - in plain talk just what is a strongly linked pair vs a weakly linked animal vs a chain vs a conjugate chain vs a link, vs a weak link vs a strong link vs simple colouring vs multicolouring vs supercolouring ! come on guys, we beginners are trying to learn to crawl here, and the solver notes on the site seem to be directed at helping the already clever solvers get even cleverer ! ok so please your comments /assistance is really really appreciated and i feel that im nearly there with simple colouring as long as it sticks to a few basic and understandable rules like basic methods to eliminate candidates up to xwing and swordfish! cheers goldie

[FAST Enterprise [Crawler]]

goldie - you're right that some of the assistance in this Forum is mumbo jumbo for relative newcomers or for non-mathematicians.

It never fails to put me in mind of the maths teacher at my grammar school in rural Shropshire. He was doubtless brilliant with numbers but he "lived on another planet" and couldn't translate his knowledge into a language that bright sixteen year-olds could understand. With his "help" and despite my subsequently having an IQ measured at 173, no less, when I was twenty and having been in Mensa since then, I failed GCE maths. Happily, after leaving school, I proceeded to teach myself the maths curriculum, in my spare time, paid the exam fee myself and passed at the first attempt.

In my view em and stuartn are the best Forum members, when it comes to straightforward and lucid explanations. Hopefully, one or both of them will be able to put you out of your misery, although I have to say that angusj.com "did it for me", for everything including colouring.

[emm]

Well I can't cope with that praise. On basic matters I can present info in a straightforward fashion, but on any advanced techniques I am a novice. Until I read tso's post above I didn't have the slightest interest in colouring and hadn't contemplated using it. I have to say that I thought his explanation was crystal clear.

I can only repeat 9x9s advice, goldie - http://angusj.com/sudoku/hints.php describes it well (and in colour).

By the way, in terms of presentation, do you have paragraphs in South Africa? It sure helps to read all those words if there are spaces sometimes. Just a thought.

[tso]

goldie5218:

It's confusing at first but it will 'click' into place for you soon. Personally, I think coloring is the most fun of the advanced tactics to use -- as you 'apply' it rather than just search for it. Once you get the hang of it, it is *very* easy to use.

And yes, some of the terminology is more confusing than the underlying logic, especially since there are many names for each tactic and different people use the same words to mean somewhat different things. It's a new science and there isn't total agreement yet. Personally, I wish we would have used chess-type notation ("if a5=5 then b4=3" is easier for me to parse than "if r1c5=5 then r2c4=3"). I still don't understand everything that goes on here and especially on the programmers forum -- and yet I've got everyone snowed here into thinking I'm an expert. Just let it wash over you and it will sink in.

Anyway, back to your question:

" ... in the sample puzzle there are three candidates (5) in the block that the single 'erasable' candidate is in, and because of this i cannot understand why that single candidate is selected for erasure."

This is because only ONE of these candidates is in the same group (row, column or box) as one of each color.

Look at the diagram again:

Code: Select all

 
  .   .   .  |  5   5   .  |  .   .   . 
  .   .   .  |  .   .   .  |  .   .   . 
  .   .   .  |  .   .   .  |  .   .   . 
-------------+-------------+------------
  5   .   .  |  5   5   .  |  .   .   5 
  5  [5]  .  |  .   5   .  |  .  +5   . 
  .   .   .  |  5   5   .  |  .   .   5 
-------------+-------------+------------
  .   .   .  |  .   .   .  |  .   .   . 
  .  -5   .  |  .   .   .  |  .   .  +5 
  5   5   .  |  .   .   .  |  .  -5   .



1) The [5] at r5c2 is in the same row as one of the +5, so if the +5's are "true", that is, if they are actually 5's, then [5] is NOT a 5.

2) The [5] is also in the same column as one of the -5, so if the -5's are "true", then [5] is NOT 5.

Since one of these two statements must be true -- this is the whole point of coloring -- then [5] must NOT be 5. No other candidate in box 4 -- or anywhere else in the grid -- is at the 'intersection' of two opposite color cells. R5c1 is in a row with a +5, but not in a row, column or box with a -5, so we cannot make a direct inference about it's value.

I'll take a look at color2 and make a separate post.

[tso]

Here's the puzzle in question -- Simple Sudoku's colors2.ss -- just before coloring is needed:



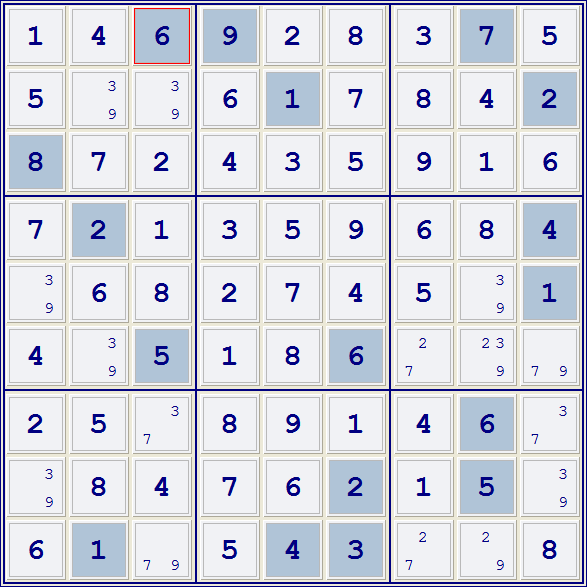
Filter for 9's:



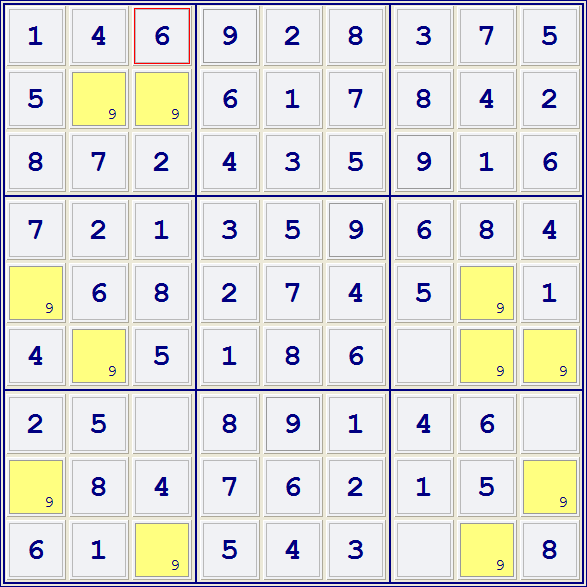
Now, we can start with nearly any of the filtered cells. For no reason at all, let's start with r2c2 and color it RED. Now color all the 'conjugates' of this first cell BLUE. Remember, two cells are conjugates if they are the only two cells in a group (row, column or box) that can contain the candidate in question. Now color all the conjugates of the BLUE cells RED. Continue until there are none left that can be colored. You should have this:




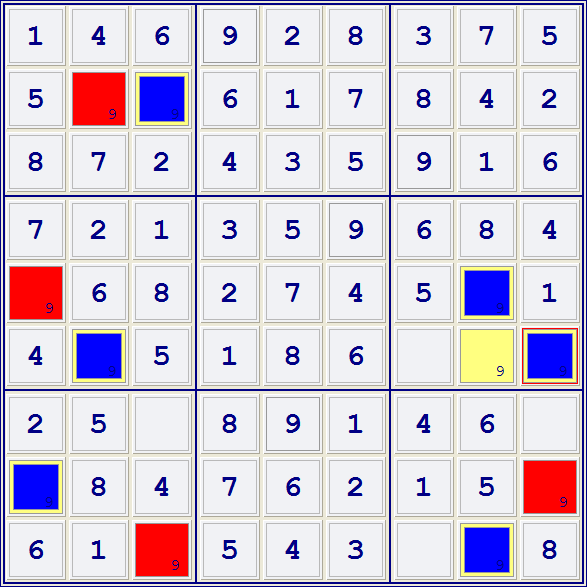
(Note that we color r5c8 blue because it is a conjugate pair with r5c1.
We color r6c9 blue because it is a conjugate pair with r8c9.)

Look, row 6, columns 2 and 9 are both BLUE! If blues are "true", that is, if the are actually filled with 5's, we would have a contradiction -- two 5's in one row. This proves that these two cell -- AND ALL OTHER BLUE CELLS -- are NOT 5's, and all the RED cells ARE 5's.

Similarly, there are two blue cells in 8th column and two blue cells in the 6th box, allowing the same inference.


When using this coloring method, there are three possible results:

1) No inference can be made.

2) Two (or more) cells in the same group are the same color -- these must be "false". All the cells of the opposite color are "true" and may be filled in.

3) One if each color "intersect" with a cell that has not been colored -- that is, a RED and a BLUE cell each are in a group with a third, uncolored cell. This third cell is eliminated. (This is what happened in color1.)

[goldie5218]

hi tso ,hi em, thanks very very much for your help with my "colour blindness' whew! got it at last thanks to you guys! much appreciated help! oh by the way em, very very sensitive topic, theres nothing wrong with South Africa !!!!!!! the problem is my poor typing skills. gotta work on my paragraph insertion. cheers and thanks again for the patience and help - goldie

[Kites]

Thanks for an excellent explanation Tso. For the first time, I also, understand Coloring.

[Karyobin]

To be honest, I read about it in Sadman's pages during my first day on this site. I thought it was obvious how it worked: colours imply on or off states. Attribute colours, search for contradictions and remove them.