The New Sudoku Players' Forum

[ronk]

do_death_blossom - reducing r2c4.<1237> by <2> dual[2]
do_death_blossom - reducing r1c9.<1478> by <4> dual[2]
do_death_blossom - reducing r2c7.<46789> by <4> dual[2]
do_death_blossom - reducing r2c8.<14578> by <4> dual[2]
do_death_blossom - reducing r2c9.<14789> by <4> dual[2]
do_death_blossom - reducing r3c8.<4567> by <4> dual[2]
do_death_blossom - reducing r2c7.<6789> by <7> dual[2]
do_death_blossom - reducing r3c1.<2567> by <7> dual[2]
do_death_blossom - reducing r3c2.<24567> by <7> dual[2]
do_death_blossom - reducing r3c8.<567> by <7> dual[2]
do_death_blossom - reducing r8c7.<246789> by <7> dual[2]
do_death_blossom - reducing r9c7.<24679> by <7> dual[2]
do_death_blossom - reducing r2c7.<689> by <8> dual[2]
do_death_blossom - reducing r8c7.<24689> by <8> dual[2]
do_death_blossom - db[2] stem cells r4c49.<2> ALS[1] -2- r3c49.<n247> ALS[2] -2- r156c7.<n2478> <47>

I can't get 14 eliminations without making the "stem cell set" r4c489. Shouldn't that be in the last line somehow?

[PIsaacson]

Ron,

I don't think adding r4c8 is required for the DB since the bi-location n2r4c49 stem works just fine to tie the 2 ALSs together on RCD 2, forming the dual-linked ALSs with the paired RCDs 24. The 14 eliminations are just the direct result of standard ALS dual-linked eliminations at that point. Allan's set/link-set logic adds the additional 2 eliminations r4c8<>1 and r4c9<>4 if you add all 7 cells using "Add/Sub Base Set -> Cell" followed by "Draw Logic as Sets, Auto" and "Allow Strong Cover Sets".

If you subsequently add r4c8 to the base set, Xsudo assigns r4c8=4 and adds the 3 additional resulting r789c8<>4 eliminations. That's more or less what I'm duplicating with my base/cover engine, but I'm having problems duplicating those direct assignments. They are (usually) caught by lower level logic after dropping out of the higher level logic passes.

Instead of adding any stems as "Add/Sub Base Set -> Cell", you can try what I've been playing with and just right click n2r4c4 and "Add/Sub Base Set -> Row" to tie the 2 ALSs on the conjugate n2r4c49. In that case, you should see that it produces all 14 standard ALS eliminations plus r4c9<>4, but omits r4c8<>1.

I don't know if that helps, or hurts in terms of explaining things.

Cheers,
Paul

[ronk]

I don't think adding r4c8 is required for the DB since the bi-location n2r4c49 stem ...

Instead of using a bilocal, I was trying to use an r4c489 "ALS". My bad.

But there is a side benefit for me. That ALS r4c489 is actually an LS, so I now understand an earlier Allan Barker triggered discussion where the left and right RCCs could be the same.

[Allan Barker]

My ALS engine found your example dual-linked ALS as a Death Blossom, but using a different stem r4c49.<2> and with 16 eliminations. I checked with Xsudo and they all appear to be found by the same base/cover set that my new base/cover engine discovered. I use different notation, but it matches exactly. The base/cover engine found 2 additional eliminations that dual-linked ALS rules didn't catch using the stem cells + all the ALS cells.

I think the "more correct" base set should just include 2r4 for the stem cells, but then it omits the r4c8<>1 elimination.

Edit This is a re-post of an earlier post that was deleted.

I now understand your death blossom, which I found as a continuous nice loop with one ALS link. This loop uses 2R4 as a base set and causes the same 14 eliminations. It also seems to be the same logic, only the name is different.

Code: Select all

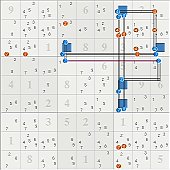
Rank 0 continuous nice loop (with ALS link) 

     (2c4)  (4b3)  (7r3)  (8c7)  (2b6)  (7c7)

2R4: 2r4c4=======================2r4c9            row base set
       |                           |           
3N4: 2r3c4=========7r3c4           |           
                     |             |           
5N7:                 |           2r5c7==7r5c7 
                     |                    |   
3N9:        4r3c9==7r3c9                  |   
              |                           |   
6N7:          |           8r6c7=========7r6c7    }
              |             |             |      }     ALS
1N7:        4r1c7=========8r1c7=========7r1c7    }
 

For the Xsudo base/cover set model you compare to:

Code: Select all

From Xsudo:
+----------------------+------------------+--------------------------+
| 9      3457    4578  | 137    6    145  | (478)    2        178-4  |
| 38     234567  45678 | 137-2  45   1245 | 69-478   15678-4  1789-4 |
| 256-7  2456-7  1     | (27)   8    9    | 3        56-47    (47)   |
+----------------------+------------------+--------------------------+
| 38     379     789   | (12)   79   6    | 5        4-1      (12-4) |
| 4      1       57    | 8      357  2357 | (27)     9        6      |
| 567    5679    2     | 4      579  157  | (78)     1378     1378   |
+----------------------+------------------+--------------------------+
| 67     4679    3     | 5      2    478  | 1        4678     4789   |
| 1      245679  45679 | 69     347  3478 | 2469-78  34678    234789 |
| 267    8       4679  | 69     1    347  | 2469-7   3467     5      |
+----------------------+------------------+--------------------------+

Pwaz 16 Candidates, Raw Rank = 2 (linksets - sets)
     7 Sets = {34N4 156N7 34N9}
     9 Links = {7r3 12r4 2c4 78c7 4c9 2b6 4b3}
     7 Eliminations -->
     r3c128<>7, r12c9<>4, r2c4<>2, r4c8<>1,

I get 7 eliminations, and, 2r4 serves no purpose.

I think what's going on is that 2r4 is not a true cover set, at least not an obvious one. It is however, a "strong" cover set. With the setting [Allow Strong Cover Sets] = ON, there will be 16 eliminations because Xsudo is using 2r4 as a strong link. When ASCS = OFF, there will be 7 eliminations, and 2r4 is no longer needed.

Back to the Death Blossum (or continuous nice loop). In this case 2R4 is really a base set and all 14 of the eliminations are there with or without allowing strong cover sets.
.