The New Sudoku Players' Forum

by **Draco** » Sun Apr 05, 2009 3:15 am

This comes from Playr.co.uk as Extreme #6-622381:

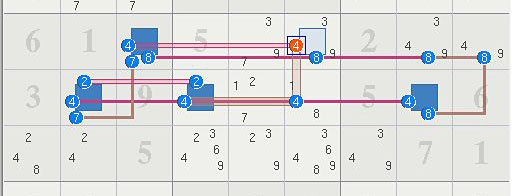
Code: Select all: ....457....1..7...9..18..5.61....2..3.9...5.6..5....71.8..52..3...7..8....386.... 28 236 268 | 2369 4 5 | 7 1 289 2458 23456 1 | 2369 239 7 | 3469 3489 2489 9 23467 2467 | 1 8 36 | 346 5 24 ----------------+-----------------+--------------- 6 1 478 | 5 379 3489 | 2 3489 489 3 247 9 | 24 127 148 | 5 48 6 248 24 5 | 23469 239 34689 | 349 7 1 ----------------+-----------------+--------------- 7 8 46 | 49 5 2 | 1 469 3 124 2469 246 | 7 139 1349 | 8 2469 5 1245 2459 3 | 8 6 149 | 49 249 7

The PMs are post-SSTS.

To be clear these puzzles are all far beyond what I can solve manually. My solver finds several potential back doors, but the nets (including one Nishino) it comes up with to crack the puzzle are pretty hairy (it takes 3 of 'em).

Any takers?

Cheers...

- drac

by **ttt** » Sun Apr 05, 2009 7:35 am

Code: Select all: *--------------------------------------------------------------------* | 28 236 268 | 2369 4 5 | 7 1 289 | | 2458 23456 1 | 2369 239 7 | 3469 3489 2489 | | 9 23467 2467 | 1 8 36 | 346 5 24 | |----------------------+----------------------+----------------------| | 6 1 478 | 5 379 3489 | 2 3489 489 | | 3 247 9 | 24 127 148 | 5 48 6 | | 248 24 5 | 23469 239 34689 | 349 7 1 | |----------------------+----------------------+----------------------| | 7 8 46 | 49 5 2 | 1 469 3 | | 124 2469 246 | 7 139 1349 | 8 2469 5 | | 1245 2459 3 | 8 6 149 | 49 249 7 | *--------------------------------------------------------------------*

I start first (not complete as usually

):
(13)r8c56=(1)r9c6-(1)r5c6=(1-27)r5c25=(2)r5c4-(2)r12c4=(2-9)r2c5=(9)r12c4-(9=4)r7c4 => r8c6<>4

ttt

by **Draco** » Sun Apr 05, 2009 8:33 am

ttt -- that exposes a nice backdoor where r9c7<>9 will crack the puzzle to singles + an open pair in b1, leaving the puzzle at singles. There are some other backdoors as well, but this is one of the more accessible ones your move exposes.

Nice... could you tell me how you decided on using what appears to be an ahp (13) to start the move? And while I am starting to get the hang of Eureka (I think), I can't quite decode what r5c6=(1-27)r5c25 signifies?

Cheers...

- drac

PS: I found a Nishino net that hits many of the same squares and gives the same result, but since I don't know how to read your chain, I can't tell if they are just close or essentially the same:

r8c6=4 r7c4=9
r8c6=4 r8c5=3 r5c5=1
r7c4=9 [r1c4<>9 r2c4<>9] r2c5=9
[r8c6<>1] + r5c5=1 [r5c6<>1] = r9c6=1
r8c6=4 [r5c6<>4] + r9c6=1 [r5c6<>1] = r5c6=8
[r2c5<>2 + r5c5<>2] = r6c5=2 r5c4=4
r5c6=8 r5c8=4
r8c6<>4

by **Luke** » Sun Apr 05, 2009 9:19 am

Code: Select all: *--------------------------------------------------------------------* | 28 236 268 |*2369 4 5 | 7 *1 289 | | 2458 23456 1 | 2369 239 7 | 3469 -9348 2489 | | 9 23467 2467 | 1 8 36 | 346 5 24 | |----------------------+----------------------+----------------------| | 6 1 478 | 5 379 3489 | 2 3489 489 | | 3 247 9 | 24 127 148 | 5 48 6 | | 248 24 5 | 23469 239 34689 | 349 7 1 | |----------------------+----------------------+----------------------| | 7 8 46 |*49 5 2 | 1 *469 3 | | 124 2469 246 | 7 139 1349 | 8 2469 5 | | 1245 2459 3 | 8 6 149 | 49 249 7 | *--------------------------------------------------------------------*

Noting conjugate (9)'s in r7: finned x-wing => r2c8<>9.

Edit to add a little loop:

Noting conjugate (6)'s in r6:
(6)r6c4=(6)r6c6-(6=3)r3c6-(group3)r12c4=(3)r6c4=>r6c4<>(249), r2c5<>3.

This type of puzzle I just have to chip away like this,

Draco, how do you know where the "back doors" are?

by **ttt** » Sun Apr 05, 2009 9:25 am

Draco wrote:... could you tell me how you decided on using what appears to be an ahp (13) to start the move? And while I am starting to get the hang of Eureka (I think), I can't quite decode what r5c6=(1-27)r5c25 signifies?

That is not the first move I found...

There is some path to crack this one then my best path based on above move, we have strong link 4’s in box 8 after that.

(1)r5c6=(1-27)r5c25=(2)r5c4 meant (1)r5c6=(1)r5c5-(27)r5c25=(2)r5c4

I’m not sure for bellow NL – please correct me:
r8c6-4-als:r8c56=1=r9c6-1-r5c6=1=als:r5c25=2=r5c4-2-r12c4=2=r2c5=9=r12c4-9-r7c4-4-r8c6 => r8c6<>4

ttt

by **aran** » Sun Apr 05, 2009 2:42 pm

Code: Select all: *--------------------------------------------------------------------* | 28 236 268 | 2369 4 5 | 7 1 289 | | 2458 23456 1 | 2369 239 7 | 3469 3489 2489 | | 9 23467 2467 | 1 8 36 | 346 5 24 | |----------------------+----------------------+----------------------| | 6 1 478 | 5 379 3489 | 2 3489 489 | | 3 247 9 | 24 127 148 | 5 48 6 | | 248 24 5 | 23469 239 34689 | 349 7 1 | |----------------------+----------------------+----------------------| | 7 8 46 | 49 5 2 | 1 469 3 | | 124 2469 246 | 7 139 1349 | 8 2469 5 | | 1245 2459 3 | 8 6 149 | 49 249 7 | *--------------------------------------------------------------------*

Some examples from this puzzle just to illustrate hidden set logic :
hidden pair
1. 48(r5c8+r4c9)=9r4c9-9r1c9=28r1c19-8r1c3=8r4c3 : =><8>r4c8
2. 48(r5c8+r4c9)=9r4c9-9r1c9=28r1c19-(8=6)r1c3-6r78c3=(6-9)r8c2=9r9c2-(9=4)r9c7 : =><4>r6c7
3. 28r1c13=6r1c3-(6=4)r7c3-(4=2)r8c3-(24=1)r8c1-(124=5)r9c1-5r9c2=(5-2)r2c2 :=><2>r2c2
hidden triple
4. 246r178c3=8r1c3-(8=2)r1c1 : =><2>r3c3
hidden quintuplet...
5. 24689r45789c8=3r4c8-(3=9)r6c7-(9=4)r9c7-(4=269)r789c8 :=><9>r2c8...but then Luke found that far more easily

by **ronk** » Sun Apr 05, 2009 3:34 pm

ttt wrote:I start first (not complete as usually ):
(13)r8c56=(1)r9c6-(1)r5c6=(1-27)r5c25=(2)r5c4-(2)r12c4=(2-9)r2c5=(9)r12c4-(9=4)r7c4 => r8c6<>4

Later ttt wrote:I’m not sure for bellow NL – please correct me:
r8c6-4-als:r8c56=1=r9c6-1-r5c6=1=als:r5c25=2=r5c4-2-r12c4=2=r2c5=9=r12c4-9-r7c4-4-r8c6 => r8c6<>4

Gee, you picked out a tough one.

Your NL is incorrect, but I don't know how write it either. It seems you've managed to find an AIC that converts to a net instead of a chain. Perhaps I'll take another look later.

While trying to rewrite your AIC, I did find this continuous loop.

Code: Select all: *--------------------------------------------------------------------* | 28 236 268 |*2369 4 5 | 7 1 289 | | 2458 23456 1 |*2369 *29-3 7 | 3469 3489 2489 | | 9 23467 2467 | 1 8 36 | 346 5 24 | |----------------------+----------------------+----------------------| | 6 1 478 | 5 379 3489 | 2 3489 489 | | 3 247 9 |*24 127 148 | 5 48 6 | | 248 24 5 | 36-249 239 34689 | 349 7 1 | |----------------------+----------------------+----------------------| | 7 8 46 |*49 5 2 | 1 469 3 | | 124 2469 246 | 7 139 1349 | 8 2469 5 | | 1245 2459 3 | 8 6 149 | 49 249 7 | *--------------------------------------------------------------------* = r2c5 =9= r12c4 -9- r7c4 -4- r5c4 -2- r12c4 =2= r2c5 = continuous loop ==> r6c4<>249, r2c5<>3 (2-9)r2c5 = (9)r12c4 - (9=4)r7c4 - (4=2)r5c4 - (2)r12c4 = loop ==> r6c4<>249, r2c5<>3

by **999_Springs** » Sun Apr 05, 2009 6:20 pm

Code: Select all: 9r9c7(-9-r9c6)(-9-r7c8=9=r7c4-9-r8c6)=4=r789c8-4-r5c8-8-r5c6-14-r8c6-3-r3c6-6-r3c23 || \__________________________________________________/ || 4r9c7-naked pair r3c67-6-r3c23 r3c23<>6

I don't really know how to indicate subsets in any form of chain notation, but this should be understandable.

by **Luke** » Sun Apr 05, 2009 6:31 pm

ronk wrote:While trying to rewrite your AIC, I did find this continuous loop.
Code: Select all
*--------------------------------------------------------------------* | 28 236 268 |*2369 4 5 | 7 1 289 | | 2458 23456 1 |*2369 *29-3 7 | 3469 3489 2489 | | 9 23467 2467 | 1 8 36 | 346 5 24 | |----------------------+----------------------+----------------------| | 6 1 478 | 5 379 3489 | 2 3489 489 | | 3 247 9 |*24 127 148 | 5 48 6 | | 248 24 5 | 36-249 239 34689 | 349 7 1 | |----------------------+----------------------+----------------------| | 7 8 46 |*49 5 2 | 1 469 3 | | 124 2469 246 | 7 139 1349 | 8 2469 5 | | 1245 2459 3 | 8 6 149 | 49 249 7 | *--------------------------------------------------------------------* = r2c5 =9= r12c4 -9- r7c4 -4- r5c4 -2- r12c4 =2= r2c5 = continuous loop ==> r6c4<>249, r2c5<>3 (2-9)r2c5 = (9)r12c4 - (9=4)r7c4 - (4=2)r5c4 - (2)r12c4 = loop ==> r6c4<>249, r2c5<>3

Luke451 wrote:Noting conjugate (6)'s in r6:
(6)r6c4=(6)r6c6-(6=3)r3c6-(group3)r12c4=(3)r6c4=>r6c4<>(249).

Ron, I think I over-looked the r2c5<>3 in the above loop. That would mean there's two loops here with the exact same eliminations!

by **Allan Barker** » Sun Apr 05, 2009 6:32 pm

And just when you begin to think, that it all begins to look the same ..........

7 Sided Broken Loop with 1 target that sees 4 guardians, with guardian appendix

Code: Select all: +--------------------+---------------------+---------------------+ | 28 236 268 | 2369 4 5 | 7 1 289 | | 2458 23456 1 | 2369 239 7 | 3469 3489 2489 | | 9 23467 2467 | 1 8 36 | 346 5 24 | +--------------------+---------------------+---------------------+ | 6 1 (4*78)| 5 379 39-4(8*)| 2 349(8) 49(8) | | 3 (2*47) 9 | (24*) 127 18(4*) | 5 (48) 6 | | 248 24 5 | 23469 239 34689 | 349 7 1 | +--------------------+---------------------+---------------------+ | 7 8 46 | 49 5 2 | 1 469 3 | | 124 2469 246 | 7 139 1349 | 8 2469 5 | | 1245 2459 3 | 8 6 149 | 49 249 7 | +--------------------+---------------------+---------------------+ (4r4) (4n6) <--- Cover Sets ---> (2r5) (4b5) 4r4c6================4r4c6===============================================4r4c6 <-- Target | | / \ 4N3 *4r4c3==7r4c3==8r4c3 | | | || || | | | 8R4: || 8r4c3=*8r4c6==8r4c8==8r4c9 | | || || || | | 8B6: || 8r4c8==8r4c9==8r5c8 | | || || | | 5N8: || 8r5c8==4r5c8 | | || || | | 4R5: || 4r5c8==4r5c2=======*4r5c6==*4r5c4 || || | 5N2: || 4r5c2==7r5c2=*2r5c2 | Appendix || || | | Guardian 7B4: 7r4c3===================================================7r5c2 | | Loop | | 5N4: 2r5c4==4r5c4 Guardians (*) Note: Broken Wing candidates shown twice to show set links (left)

by **Draco** » Sun Apr 05, 2009 7:59 pm

Luke451 wrote:Draco, how do you know where the "back doors" are?

It's just code + CPU cycles. My solver has a scoring algorithm that is reasonably stable (not as useful as SE because it does not support as many techniques, but it does the job). With a scoring algorithm, you simpoly loop through the puzzle to see what each new move does (I got the idea from a discussion in the Solver thread).

It is interesting to see how different moves cause different sections of the grid to "collapse" (i.e. create a new backdoor). For a puzzle like this one, it is also kinda' slow (5 - 10 seconds to test/score the puzzle and come up with a "top 10" list). I've been thinking about creating grapics that visually show how the puzzle progresses, but have not moved beyond the thought stage there.

Cheers...

- drac

by **Draco** » Sun Apr 05, 2009 8:19 pm

Allan Barker wrote:And just when you begin to think, that it all begins to look the same ..........

7 Sided Broken Loop with 1 target that sees 4 guardians, with guardian appendix

Wow... I am not even sure how to read that, but with the graphics I imagine I'll figure it out. No help (for me anyway) just yet pls.

I do have one question Allan -- how is a 7-sided loop different than a network?

Thx...

- drac

by **Draco** » Sun Apr 05, 2009 9:09 pm

Not utilizing the backdoors, but here's a chain + simple net that use links on 2's and 8's to show r2c9<>2, r3c3<>2 (from the orignial PMs):

------ Chain ------
r1c1=2 [r3c2<>2 r3c3<>2] r3c9=2
------ Simple Net ------
r1c1=8 [r6c1<>8] r4c3=8 r6c6=8
r4c3=8 r3c3=7
r6c6=8 [r5c6<>8] r5c8=8
r1c1=8 [r2c1<>8] + r5c8=8 [r2c8<>8] = r2c9=8

I've tried to combine this will all the other eliminations people have posted to come up with a merged set of PM's (hope I got them all):

Code: Select all: 28 236 268 | 2369 4 5 | 7 1 289 2458 3456 1 | 2369 29 7 | 3469 348 489 9 2347 47 | 1 8 36 | 346 5 24 --------------+----------------+-------------- 6 1 478 | 5 379 389 | 2 349 489 3 247 9 | 24 127 148 | 5 48 6 248 24 5 | 36 239 34689 | 39 7 1 --------------+----------------+-------------- 7 8 46 | 49 5 2 | 1 469 3 124 2469 246 | 7 139 139 | 8 2469 5 1245 2459 3 | 8 6 149 | 49 249 7

Cheers...

- drac

by **ronk** » Sun Apr 05, 2009 11:35 pm

Allan Barker wrote:7 Sided Broken Loop with 1 target that sees 4 guardians, with guardian appendix

Congratulations on a very nice find. Most of us think of the "broken wing" in terms of a single digit, but the principle certainly holds for multi-digit broken wings as well. To your knowledge, has anyone ever posted a multi-digit BW before :?:

Luke451 wrote:I think I over-looked the r2c5<>3 in the above loop. That would mean there's two loops here with the exact same eliminations!

Right you are and, with only three strong inferences, that's an elegant continuous loop. Suggest you edit that add'l elimination into your post.

by **aran** » Mon Apr 06, 2009 12:02 am

Allan Barker wrote:7 Sided Broken Loop with 1 target that sees 4 guardians, with guardian appendix
Code: Select all
+--------------------+---------------------+---------------------+ | 28 236 268 | 2369 4 5 | 7 1 289 | | 2458 23456 1 | 2369 239 7 | 3469 3489 2489 | | 9 23467 2467 | 1 8 36 | 346 5 24 | +--------------------+---------------------+---------------------+ | 6 1 (4*78)| 5 379 39-4(8*)| 2 349(8) 49(8) | | 3 (2*47) 9 | (24*) 127 18(4*) | 5 (48) 6 | | 248 24 5 | 23469 239 34689 | 349 7 1 | +--------------------+---------------------+---------------------+ | 7 8 46 | 49 5 2 | 1 469 3 | | 124 2469 246 | 7 139 1349 | 8 2469 5 | | 1245 2459 3 | 8 6 149 | 49 249 7 | +--------------------+---------------------+---------------------+

Allan, less good, one could also apply anti-guardian logic :
Guardian logic : preservation of a valid loop=>guardians required=>eliminate anything seen by all guardians
Anti-guardian logic : starting with the elimination candidate (that's the weak part of the story !) ignore all anti-guardians (ie anything which if true eliminates the elim candidate).
Giving :
4r4c6-(4=2)r5c4-(2=47)r5c2.
Then 7r5c2=8r4c3(4*r4c3 ignored)-8r4c89=(8-4)r5c8=4r5c2(4*r5c46 ignored). Contradiction ie to preserve 4r4c6, r5c2 must be both 7 and 4=><4>r4c6.

The New Sudoku Players' Forum

Another SE 8.3

Another SE 8.3