The New Sudoku Players' Forum

[surbier]

Hi,
This is my first post in this forum.

I usually solve sudokus using pencil and paper. For advanced methods like nice loops there
exist user-friendly graphical methods/hints helping to spot the strong and weak inferences for closing the loop.
On the other hand I find it very difficult to spot ALS within the crowded field of candidates.
Does anybody know some simple pencil drawing tricks for better spotting of ALS ?

Thanks, surbier

[David P Bird]

Hello Surbier, Manually finding every ALSs opportunity is difficult and tedious as there are so many of them. I find it easier to look for their complements which are almost tuples (pairs, triples, quads). The most common and the most productive are Almost Hidden and Almost Naked Pairs which are what I go for first. Only later if I'm still struggling do I look for the others.

I mark single candidates that if false will leave a pair. I call these triggers as they will lead to either the ALS or the Pair being usable for extending an inference chain. With practice you'll then start to spot almost triples too.

You won't catch every ALS this way, but you'll get most of the useful ones!

[champagne]

Hi,
Does anybody know some simple pencil drawing tricks for better spotting of ALS ?

My experience is that most interestng ALS/AHS are those having two cells and three digit with one compulsory.

You can start with that family, you should do some miles and there are not hundreds of them. They can be used wthin a "pencil mark" constraint.

Another point is what for

I know at least two ways to handle ALS.

Historically the first one is to consider couples of ALS. If you choose that process, my recommendation is not very efficient.

The second one is to couple them with the counterpart, an AHS, what I am doing in full tagging.

With the restricted family I suggest to learn first, the counterpart is ALS/AHS as well.

In the most general case, the counterpart AHS (AC for me or "Almost cell" ) behave like a cell. This offers wide possibilities than I can develop if you are interested.


But extending the scope will not keep you very long within "pencil mark" limits, unles you use a A4 or A3 form.


champagne

[DonM]

Surbier, for a start you might find this helpful- it is the only ALS tutorial that I know of that provides several clear graphical examples. As does the author of that tutorial, I also find it easier to think in terms of ALS Chains since the construct of the ALS xz-rule (2 ALS sets), ALS xy-wing rule (3 sets) and ALS xy-chain (>=4 sets) are all the same- the only difference is the number of sets and restricted commons:

http://www.sudoku.org.uk/SudokuThread.asp?fid=4&sid=10326&p1=1&p2=11

ALS Chains are in a category that I call Pattern A solving which refers to pure, visible, 'what is' patterns such as naked pairs, xy-wings and the like (as opposed to Pattern B solving which refers to the nice loop & AIC chains). Over the last year or two I have been concentrating on manual solving only puzzles at the > SE=8 level, beyond the SSTS point (Simple Sudoku limit) which, for me at least, don't lend themselves easily to pencil & paper solving, but lately I decided to take some time out & go back to my collection of Los Angeles Times Diabolicals (usually SE < 7.4) and 'refresh' my basic method Pattern A solving skills & for this situation, I find that pencil & paper works just fine.

IMO, ALS Chains are the most powerful method available for this type of solving (one reason being that in their most powerful form, they are much like grouped nice loops or AICs), but I find they are more likely to be both useful & reasonably easy to find in end-stage solving when there are likely to be more bivalue & trivalue cells. It's easier to explain my procedure with some graphics. The following is from a real-world solution of the LA Times diabolical from 04/15/07. In this case, two 4-set ALS Chains broke the puzzle:



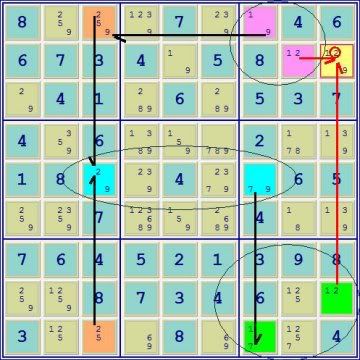
The graphic is pretty self-explanatory: The ALS sets are distinguished by colored cells and the black lines show the connection between the restricted commons. The flanking pink & green sets 'point' to & thus eliminate the 2 in r2c9. One would think that finding a 4-set ALS Chain (aka ALS xy-chain) might be difficult using only pencil & paper, but it actually isn't if you practice a lot. Often, since this can be the most strategic point in the solving, I will first make a copy of the puzzle to work on since I'm going to be marking up the puzzle quite a bit. I start by circling with light pencil potential sets, particularly those where there are 2 bivalue cells in which only one digit is duplicated (as opposed to almost naked pairs where 2 digits are duplicated) because it is going to be easier to find restricted common connections with these types of sets eg. the green, blue, and pink sets above. Next I circle almost naked pair sets such as the orange set above (couldn't find an easy way to circle the set in the graphic ).

Finally, I isolate other sets that might be useful such as perhaps the set in r3c46 (2,8,9), but here I draw a square around them. Now I am able to look at the puzzle and see the isolated sets & see what I can make of them. It takes a bit of practice to decide which method works best for you, but if you understand the underlying principle of ALS Chains and find the best way of isolating potential sets, you find that they start to jump out at you even with pencil & paper. If you get to the point where you can find 4-set chains, then something like a 2-set ALS xz-rule will be a piece of cake!



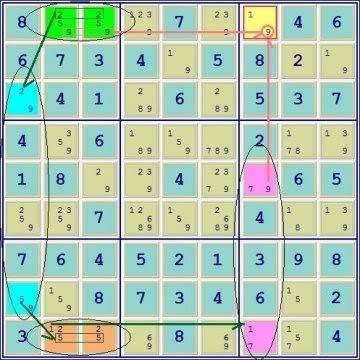
The final ALS Chain above which totally dismantles this puzzle is a good example of why I first start looking for 2 bivalue cells where only one of the digits is duplicated. Because in these types of sets there are 2 single digits such as the 2 and the 5 in the blue set and the 1 and the 9 in the pink set, it is more likely that restricted common connections can be found between otherwise distant sets. Note how the blue set connects the green & orange sets that are some distance apart.

[Myth Jellies]

Don, I like your concept of using recognizable subcomponents, such as ALSs, and chaining them together and calling it type A. Just wanted to point out that most of the AIC components are ALS's as well. For example, a bivalue cell is an ALS (almost naked single), while a bilocated digit is an AHS (almost hidden single) which will have a complementary ALS that you could always use instead if you prefer. Thus you can construct an AIC in the same Type A way you construct an ALS chain. I actually encourage people to do that as that is the way I find AICs myself.

Another tip. If you like 3D-Medusa coloring (or tagging), make a big grid on a piece of notebook paper and then write your candidates vertically down the sides of the cells. That way you can easily add uppercase and lowercase characters next to the candidates to represent conjugate colors. Often an almost hidden set will contain a bilocated digit, so coloring can help direct your sight to finding them.

[DonM]

Don, I like your concept of using recognizable subcomponents, such as ALSs, and chaining them together and calling it type A. Just wanted to point out that most of the AIC components are ALS's as well. For example, a bivalue cell is an ALS (almost naked single), while a bilocated digit is an AHS (almost hidden single) which will have a complementary ALS that you could always use instead if you prefer. Thus you can construct an AIC in the same Type A way you construct an ALS chain. I actually encourage people to do that as that is the way I find AICs myself.

Another tip. If you like 3D-Medusa coloring (or tagging), make a big grid on a piece of notebook paper and then write your candidates vertically down the sides of the cells. That way you can easily add uppercase and lowercase characters next to the candidates to represent conjugate colors. Often an almost hidden set will contain a bilocated digit, so coloring can help direct your sight to finding them.

Good tips Myth. Now I understand a little more why in a conversation some time ago you were determined that AIC-creation be looked on also as a form of pattern solving.

[surbier]

Thank you all for explaining your personal favorite technique.

Thank you DonM for your detailed graphics and the valuable references.
I was not aware that the three apparently different types of ALS (xz, xy and xy-chain) are well covered by the concept of ALS-chains.

I initially thought of a simple and small size graphic with circles for bi-value cells (almost naked single),
and lines for ALS composed of two or more cells.
My underlying intend was to detach the constellation from the cell content.
But I realized that having e.g. in one line three cells like
[12] .. [23] .. [34], there would be 6 possible ALSs, which would end up
in a crowed field of many parallel lines. This is no good idea.

Anyway, I practiced a little bit the spotting of ALS-chains with a low number of cells like bi-value cells and almost naked pairs.
I realized that it is not only to spot the complements (~ the constellation) of the ALS but also to find the restricted common (~ the link). When you can remember or mark the initial flanking ALS and build up a chain that hopefully ends up in an elimination it is not necessary to go for an A4 size additional paper.
But Certainly for higher grades and when leaving the canceled candidates without obliteration.

[Glyn]

I have split of some off topic posts concerning an application of AALS to a thread French Forum Puzzle #283. Please post in the relevant thread.