The New Sudoku Players' Forum

[Luke]

I’m wondering if have the following correct. I can’t find much info on this particular situation.

It’s my understanding that if an alternating inference chain begins and ends on a strong link in the same house, you can make the following conclusion: the start value cannot be in the end cell, and the end value cannot be in the start cell.

In this puzzle the chain starts with a strong link on 9 and ends with a strong link on 8, both in the same column.

Code: Select all

Ruud's Daily Nightmare Oct 1,2007.
007103000080050079006000000002570060000000000030012500000000600450090030000805100
 
 *--------------------------------------------------------------------*
 | 259    249    7      | 1      248    3      | 248    2458   6      |
 | 123    8      134    | 26     5      46     | 234    7      9      |
 | 235    24     6      | 79     248    79     | 2348   12458  12345  |
 |----------------------+----------------------+----------------------|
 | 189    149    2      | 5      7      489    | 3489   6      134    |
 | 189    7      5      | 3      6      489    | 2489   1248   124    |
 | 6      3      489    | 49     1      2      | 5      48     7      |
 |----------------------+----------------------+----------------------|
 | 12389  129    1389   | 47     34     147    | 6      459    458    |
 | 4      5      18     | 26     9      16     | 7      3      28     |
 | 7      6      39     | 8      234    5      | 1      249    24     |
 *--------------------------------------------------------------------*
9[r6c3]=9[r6c4]-4[r6c4]=4[r5c6|r4c6]-4[r2c6]=6[r2c6]-6[r8c6]=6[r8c4]-2[r8c4]=2[r8c9]-8[r8c9]=8[r8c3].  9 cannot be in end cell,8 cannot be in start cell,therefore r6c3 <> 8.


Thumbnail:


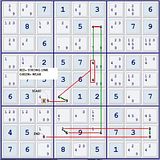
All I have to go on that this is correct is the solution, since none of my solving programs see it. Is this a legit strategy?

(BTW, I am aware there's a grouped x-cycle on 4 that accomplishes much the same thing.)

[daj95376]

9 cannot be in end cell,8 cannot be in start cell,therefore r6c3 <> 8

If 9 exists in [r8c3], then [r8c3] is no longer a bivalue cell, your chain doesn't exist, and you can't draw any conclusions.

Your chain shortened and one link added:

Code: Select all

r6c3 =9= r6c4 =4= r45c6 -4- r2c6 -6- r8c6 -1- r8c3 -8- r6c3  =>  [r6c3]<>8


An alternate chain that you might like better:

Code: Select all

r6c3 =4= r2c3 =1= r2c1 -1- r45c1 =1= r4c2 =4= r6c3  =>  [r6c3]=4  =>  [r6c3]<>89


[hobiwan]

Is this a legit strategy?

Yes, your chain is perfectly valid as is the elimination, but since most solvers show only the shortest chain for a specific elimination they won't show your chain. My solver for instance gives me:

Code: Select all

Discontinuous Nice Loop r6c3 -8- r8c3 -1- r7c2 =1= r4c2 =4= r6c3 => r6c3<>8

which translated to the technique (and notation) you used would read:

Code: Select all

4[r6c3]=4[r4c2]-1[r4c2]=1[r7c2]-1[r8c3]=8[r8c3]

[Luke]

Your chain shortened and one link added:

Code: Select all

r6c3 =9= r6c4 =4= r45c6 -4- r2c6 -6- r8c6 -1- r8c3 -8- r6c3  =>  [r6c3]<>8


Yes, that's better. Human paper and pencil solving makes for some extra work sometimes. This does use the same concept, so I'm glad I had the basic idea right .

Now, when looking for chains like this, I only know of four different ways to come to an elimination:
1. The method described above (Begin and end on strong links in same house.The beginning and ending values do not have to be the same. The start value cannot be in the end cell, and the end value cannot be in the start cell.)
2. Begin and end on strong links on the same value, same cell (That value must be true.)
3. Begin and end on weak links on the same value, same cell (That value must be false.)
4. Begin and end on strong links on the same value, but not in the same house. Any candidate that can see both beginning and ending cells gets zapped, pincer style.

I think 2 and 3 are usually called discontinuous nice loops.

That's the extent of my use of these chains, but something tells me I'm missing out on half the fun, as usual.

[daj95376]

That's the extent of my use of these chains, but something tells me I'm missing out on half the fun, as usual.

From my current notes on basic chains. Peer cell assignments are included because my solver doesn't track chain eliminations other than an initial elimination. So, I have to know where assignments force key eliminations. Except for chain type (5), all of the chains start and end in the same cell.

===== ===== ===== Basic Chain Terminology and NL Notation ===== ===== =====

Code: Select all

Strong Inference (SI):  ~A =>  B
Weak   Inference (WI):   A => ~B

Strong Link (SL):  e.g., ( bilocation  []=n=[] ) or ( bivalue cell  m-[]-n )
Weak   Link (WL):  e.g., ( peers       []-n-[] ) or ( ?-value cell  m=[]=n )

Sudopedia:  a SL can be used for SI or WI, but a WL can only be used for WI

Myth Jellies' Alternating Inference Chain (AIC):  SI, WI, (alternating until) SI
   -- bidirectional   (a chain consisting of an odd number of SL's is an AIC)


Code: Select all

[cell]   =>   starting cell
[peer]   =>   a peer cell of [cell]
[!rcb]   =>   a cell that's not [cell], nor a peer of [cell]

1) [cell]=n= ... =n=[peer]-n-[cell] -- continuous loop w/side-effect eliminations

2) [cell]=n= ... =m=[peer]-m-[cell] -- [cell] <> m

3) [cell]=n= ...          =m=[cell] -- continuous loop w/side-effect eliminations
                                       [cell] =  mn   is one side-effect

4) [cell]=n= ...          =n=[cell] -- [cell] =  n

5) [cell]=n= ...          =n=[!rcb] -- (peers_of_[cell] AND peers_of_[!rcb]) <> n

6) [cell]-n- ...          =n=[cell] -- continuous loop w/side-effect eliminations
                                       ronk doesn't think it's viable

7) [cell]-n- ... =m=[peer]-m-[cell] -- continuous loop w/side-effect eliminations
                                       [cell] must be bivalue {mn}

8) [cell]-n- ... =n=[peer]-n-[cell] -- [cell] <> n

9) [cell]-n- ...          =m=[cell] -- [cell] <> n