Philip Beeby presents what he calls 'Complex AICs' . See section D in :
http://www.philsfolly.net.au/chain_help.htm
Starting with an IF statement, one can, sometimes with advantage, keep a memory of configurations at each stage of the chain. Then one may obtain exclusion(s) not seen with 'Simple AICs'.
His example is helpful and he points out that 'most' Complex AICs are not bi-directional.
Now, it may be that some Complex AICs can be seen as bi-directional but the logic may be far more elaborate to do so.
AIC and TDP
41 posts
• Page 2 of 3 • 1, 2, 3
Re: AIC and TDP
by ghfick » Thu Dec 26, 2019 9:24 pm
- ghfick
- Posts: 233
- Joined: 06 April 2016
- Location: Calgary, Alberta, Canada youtube.com/@gordonfick
Re: AIC and TDP
by SpAce » Thu Dec 26, 2019 9:36 pm
Hi 999_Springs,
I'm breaking my pledge again, but I guess I may have to make an exception for this thread if the discussion continues.
I can't. That's what I've been saying. I can't think of a strictly unidirectional chain or a net of any kind. That's why most of the forcing chains/nets Hodoku finds are available as mirrored contradictions and verities. Not all, though, but I think this is the reason:
I guess such artificial restrictions are why Hodoku finds some nets as one or the other kind only, and why it doesn't find nets that require multi-krakens both ways at all. (Thank goodness, totuan does!
).
Exactly. As long as the ANDs and ORs are used properly, any chain or net is readable (and logically correct) both ways -- even things like memory chains, and probably even Denis' oriented chains (never tried but I see why not -- they look like memory chains to me).
Btw, did you see my matrix translation of totuan's net? It also shows clearly the dual nature by splitting the net into two ORed sub-matrices (i.e. a block triangular matrix, BTM). Its correctness was confirmed by Cenoman, and I'm pretty sure there's no simpler way to write it as a matrix. I conjecture that Hodoku only finds nets that can be written as a single triangular matrix (TM), which excludes nets with such unavoidable OR-branches. Here's another BTM I wrote for totuan's beautiful move here:
The matrix form turned out to be surprisingly simple (it's not quite one-to-one translation, but almost). If non-square matrices were accepted, it could even be compacted into an 8x9 BTM (harder to read, though):
Who would've thunk that, given the complexity of the move? (In this case there are many other reasons besides the BTM nature why Hodoku would never find such a move.)
Is a non-native English speaker like myself or Robert supposed to know such a subtle detail? If I were using the Google translator, like Robert, I would get exactly the same translation with or without the comma -- and that translation would be ambiguous. That's not my excuse though.
I did see the comma and knew what it should mean, which is why I said that interpretation seemed more likely. However, I gave daVid the benefit of the doubt because I thought it was the worse possibility. I haven't seen anyone else define forcing chains to only include assumptive contradiction chains, and I don't think such a non-standard definition makes much sense anyway. So, maybe it was in fact unambiguously defined, but in that case I must repeat this part:
It's wrong also because no chain is truly unidirectional, as discussed above. If someone claims otherwise, they should provide a counter-example or define more clearly what they mean by "unidirectional".
I'm breaking my pledge again, but I guess I may have to make an exception for this thread if the discussion continues.
999_Springs wrote:can someone enlighten me on why a forcing chain (whether it's an aic or not) would ever not be reversible?
I can't. That's what I've been saying. I can't think of a strictly unidirectional chain or a net of any kind. That's why most of the forcing chains/nets Hodoku finds are available as mirrored contradictions and verities. Not all, though, but I think this is the reason:
one could put a natural condition on the reversibility of a chain by disallowing any "or" statements in the chains and only allowing "and" statements (which is how SE organises its chain descriptions), which in this case would mean the second chain isn't reversible; or using only one "or" statement to be used at the beginning such as in kraken row/column/blocks with 3+ branches.
I guess such artificial restrictions are why Hodoku finds some nets as one or the other kind only, and why it doesn't find nets that require multi-krakens both ways at all. (Thank goodness, totuan does!
). but in some cases it can be clear and insightful to write chains with "or" statements in them which i can see in some of ttt/totuan's diagrams like this one as well as some solutions in the daily puzzles that use the | symbol in chain notation which is a clever way to avoid writing branching in the chain
Exactly. As long as the ANDs and ORs are used properly, any chain or net is readable (and logically correct) both ways -- even things like memory chains, and probably even Denis' oriented chains (never tried but I see why not -- they look like memory chains to me).
Btw, did you see my matrix translation of totuan's net? It also shows clearly the dual nature by splitting the net into two ORed sub-matrices (i.e. a block triangular matrix, BTM). Its correctness was confirmed by Cenoman, and I'm pretty sure there's no simpler way to write it as a matrix. I conjecture that Hodoku only finds nets that can be written as a single triangular matrix (TM), which excludes nets with such unavoidable OR-branches. Here's another BTM I wrote for totuan's beautiful move here:
totuan diagram: Show
my matrix: Show
The matrix form turned out to be surprisingly simple (it's not quite one-to-one translation, but almost). If non-square matrices were accepted, it could even be compacted into an 8x9 BTM (harder to read, though):
8x9 pseudo-BTM: Show
Who would've thunk that, given the complexity of the move? (In this case there are many other reasons besides the BTM nature why Hodoku would never find such a move.)
space i disagree that this is unclear since the commas before "which" and after "direction" clearly indicate that it applies as a descriptor for all forcing chains. if the commas weren't there then it would be a specifier for one type of them. this is standard usage.
Is a non-native English speaker like myself or Robert supposed to know such a subtle detail? If I were using the Google translator, like Robert, I would get exactly the same translation with or without the comma -- and that translation would be ambiguous. That's not my excuse though.
I did see the comma and knew what it should mean, which is why I said that interpretation seemed more likely. However, I gave daVid the benefit of the doubt because I thought it was the worse possibility. I haven't seen anyone else define forcing chains to only include assumptive contradiction chains, and I don't think such a non-standard definition makes much sense anyway. So, maybe it was in fact unambiguously defined, but in that case I must repeat this part:
SpAce wrote:If you did in fact mean that all forcing chains are unidirectional and assumptive, then you were simply wrong (or using a very personal definition, which amounts to the same thing).
It's wrong also because no chain is truly unidirectional, as discussed above. If someone claims otherwise, they should provide a counter-example or define more clearly what they mean by "unidirectional".
-
SpAce - Posts: 2671
- Joined: 22 May 2017
Re: AIC and TDP
by Mauriès Robert » Thu Dec 26, 2019 10:32 pm
Hi 999_Springs,
The complex chains used with the TDP are generally not bidirectional. Here is an example with the puzzle below on which I plotted by a green color a complex chain obtained by assuming 6r1c2 false. The chain (see diagram) leads to 4r9c2 which eliminates 4r1c2.
However, if you do -4r9c2, you can't go back up the chain.
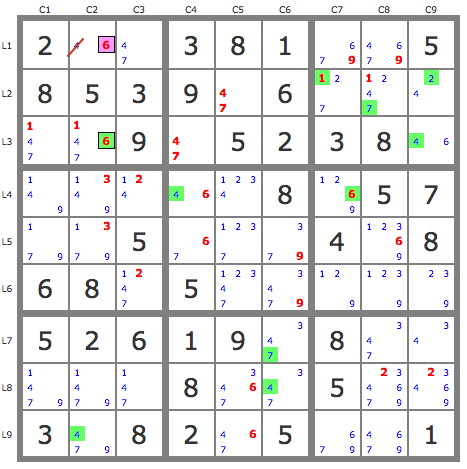
Phil gives another example (http://www.philsfolly.net.au/chain_help.htm) but there are many others.
Sincerely
Robert
The complex chains used with the TDP are generally not bidirectional. Here is an example with the puzzle below on which I plotted by a green color a complex chain obtained by assuming 6r1c2 false. The chain (see diagram) leads to 4r9c2 which eliminates 4r1c2.
However, if you do -4r9c2, you can't go back up the chain.
- Code: Select all
- - - - - - - - - - - - - -
/ / \
-6r1c2->6r3c2->4r3c9->2r2c9- - - - - - - - ->1r2c7->7r2c8->7r7c6->4r8c6->4r9c2
\ / /
\ >6r4c7>79r19c7 /
\ / /
>4r4c4- - - - - - - - - - - - - - - - -
Phil gives another example (http://www.philsfolly.net.au/chain_help.htm) but there are many others.
Sincerely
Robert
- Mauriès Robert
- Posts: 603
- Joined: 07 November 2019
- Location: France
Re: AIC and TDP
by eleven » Thu Dec 26, 2019 11:02 pm
Since SpAce is not here, I have to repeat myself at least the 5th time:
As 999_Springs said, each forcing chain is just written unidirectional, but is logically reversible.
A => B is equivalent to (not B) => (not A)
The question is, if the chain uses remembering, or - more generally - branching, which leads to a net, e.g. in a simple form
The reverse is
If these are allowed, forcing chains cannot be translated into basic AIC's, with the advantage, that they "can more" than those, and the disadvantage, that other bidirectional features cannot be used this way (like loop eliminations).
This seems to be, what David meant with "unidirectional", and it is not, what simple forcing chains are.
If "simple" forcing chains are those, which do not use branching, each basic AIC can be written as a pair of either-or forcing chains and vice versa.
E.g. you can write the AIC
as
So A or X must be true.
(where you can split the AIC at any '=' node)
So there is no logical difference between basic AIC's and non branching double forcing chains (and AIC krakens are logically the same as multiple simple forcing chains, where one of the starting points must be true).
The complexity with both notations comes with branching. It is still reversible, but normally one direction is easier to read.
You can also reverse complex forcing chains, which lead to a contradiction, in order to get a solution without the contradiction, e.g. if the contradiction is an empty cell, you can always reverse it with n forcing chains for the n candidates of the cell (but this can be harder to follow).
As 999_Springs said, each forcing chain is just written unidirectional, but is logically reversible.
A => B is equivalent to (not B) => (not A)
The question is, if the chain uses remembering, or - more generally - branching, which leads to a net, e.g. in a simple form
- Code: Select all
C => ... => D G
A => ... B => and and => or => J
E => ... => F H => I
The reverse is
- Code: Select all
(not G) (not D) => ... => (not C)
(not J) => and => or or => (not B) => (not A)
(not I) => (not H) (not F) => ... => (not E)
If these are allowed, forcing chains cannot be translated into basic AIC's, with the advantage, that they "can more" than those, and the disadvantage, that other bidirectional features cannot be used this way (like loop eliminations).
This seems to be, what David meant with "unidirectional", and it is not, what simple forcing chains are.
If "simple" forcing chains are those, which do not use branching, each basic AIC can be written as a pair of either-or forcing chains and vice versa.
E.g. you can write the AIC
- Code: Select all
A = B - ... C - D = E - F = ... = X
as
- Code: Select all
Either D => (not C) => .. = (not B) => A
Or E => (not F) => .. => X
So A or X must be true.
(where you can split the AIC at any '=' node)
So there is no logical difference between basic AIC's and non branching double forcing chains (and AIC krakens are logically the same as multiple simple forcing chains, where one of the starting points must be true).
The complexity with both notations comes with branching. It is still reversible, but normally one direction is easier to read.
You can also reverse complex forcing chains, which lead to a contradiction, in order to get a solution without the contradiction, e.g. if the contradiction is an empty cell, you can always reverse it with n forcing chains for the n candidates of the cell (but this can be harder to follow).
- eleven
- Posts: 3173
- Joined: 10 February 2008
Re: AIC and TDP
by SpAce » Fri Dec 27, 2019 1:30 am
Hi Gordon,
Like I said above, I remain active on this thread for now.
His "Complex AICs" on that page are not AICs at all. His example is a very poorly written memory chain without any indication that it's a memory chain (which makes it the worst kind). Memory chains are not valid AICs, even if written more correctly. A crucial requirement for an AIC is that every node is linked only to its adjacent nodes. Memory chains perform quantum jumps which automatically excludes them. Actual complex AICs are valid AICs that use complex features like split-nodes or nested chains.
I'm sorry to say but his example is horrible, and what he says is completely false. Correctly written chains are always bidirectional, memory chains included. Don't believe everything you read. And please don't follow Phil's lead in calling invalid AICs (like memory chains) "Complex AICs".
All real AICs are natively bidirectional no matter how complex they are. Properly written memory chains too. Let's look at Phil's example (and ignore that there are much simpler ways to get the same elimination).
Here's Phil's "Complex AIC" (red indicates a major problem, blue an inefficiency):
Here's how it should be written as a proper memory chain (two stored memories):
1) Memory chain:
That's trivial to write correctly, and it's perfectly bidirectional if you know how to read it. Valid AICs are a bit harder to write:
2) AIC with split-nodes:
3) AIC with nested chains:
As AICs, both of them are natively bidirectional, of course.
None of the above is a great way to depict such a relatively complex chain, though. An honest double-kraken would be clearer:
4) Double Kraken (3R3 + 8N5):
Is that bidirectional? It sure is. You can start at any end point (assume it false) and one of the others will be forced. In other words, it works exactly like an AIC, except that it has multiple end points. The logic is easy to follow in a matrix as well:
If one really wants (why?), it can also be turned into a contradiction net (Nishio):
6) Contradiction net:
Is that bidirectional? Of course. If you reverse it, it's the same kraken as before with the elimination included.
I wrote those examples quickly, so I don't guarantee that they're flawless.
Now, would someone have an actual example of a chain that isn't bidirectional?
Like I said above, I remain active on this thread for now.
ghfick wrote:Philip Beeby presents what he calls 'Complex AICs' .
His "Complex AICs" on that page are not AICs at all. His example is a very poorly written memory chain without any indication that it's a memory chain (which makes it the worst kind). Memory chains are not valid AICs, even if written more correctly. A crucial requirement for an AIC is that every node is linked only to its adjacent nodes. Memory chains perform quantum jumps which automatically excludes them. Actual complex AICs are valid AICs that use complex features like split-nodes or nested chains.
His example is helpful and he points out that 'most' Complex AICs are not bi-directional.
I'm sorry to say but his example is horrible, and what he says is completely false. Correctly written chains are always bidirectional, memory chains included. Don't believe everything you read. And please don't follow Phil's lead in calling invalid AICs (like memory chains) "Complex AICs".
Now, it may be that some Complex AICs can be seen as bi-directional but the logic may be far more elaborate to do so.
All real AICs are natively bidirectional no matter how complex they are. Properly written memory chains too. Let's look at Phil's example (and ignore that there are much simpler ways to get the same elimination).
- Code: Select all
.-----------------------.----------------------.-------------------------.
| 359 4 7 | a3[5]9 8 29 | 239 6 1 |
| 13589 6 123589 | 23479 379 12479 | 23489 2358 234589 |
| 13589 c^35 123589 | 6 b*359 1249 | 7 2358 234589 |
:-----------------------+----------------------+-------------------------:
| 6 2 489 | 48 1 3 | 5 7 489 |
| 34789 d37 3489 | 2478 79 5 | 123489 1238 6 |
| 345789 1 34589 | 2478 6 24789 | 23489 238 23489 |
:-----------------------+----------------------+-------------------------:
| 2 8 356 | 379-5 4 679 | j13 j13(5) 357 |
| f37 9 36 | 1 g357 678 | 238 4 23578 |
| 14 eh357 14 | h378 2 78 | 6 9 i3578 |
'-----------------------'----------------------'-------------------------'
Here's Phil's "Complex AIC" (red indicates a major problem, blue an inefficiency):
philsfolly wrote:(5)r1c4 = r3c5 - (5=3)r3c2 - (3=7)r5c2 - r56c1 = r8c1 - (57=3)r8c5 - r9c4 = r9c9 - (3=5)r7c78 => -5 r7c4
Here's how it should be written as a proper memory chain (two stored memories):
1) Memory chain:
(5)r1c4 = r3c5* - (5=3^)r3c2 - (3=7)r5c2 - r9c2 = r8c1 - (7|*5=3)r8c5 - r9c4^2 = r9c9 - (3=15)r7c78 => -5 r7c4
That's trivial to write correctly, and it's perfectly bidirectional if you know how to read it. Valid AICs are a bit harder to write:
2) AIC with split-nodes:
(5)r1c4 = r3c5 - (5=37)r35c2 - (3|7)r9c2 = (7)r8c1&(3)r9c49 - (7|3)r8c5&(31)r7c78 = (5)r8c5|r7c8 => -5 r7c4
3) AIC with nested chains:
[(5=13)r7c78 - r9c9 = r9c2 - (3=5)r3c2 - r3c5 = (5)r1c4] = (3)r9c4 - (3)r8c5 = [(5=7)r8c5 - r8c1 = r9c2 - (7=35)r53c2 - r3c5 = (5)r1c4] => -5 r7c4
As AICs, both of them are natively bidirectional, of course.
None of the above is a great way to depict such a relatively complex chain, though. An honest double-kraken would be clearer:
4) Double Kraken (3R3 + 8N5):
- Code: Select all
(3)r9c2 - (3=5)r3c2 - r3c5 = (5)r1c4 *
||
(3)r9c4 - (3)r8c5
|| ||
|| (5)r8c5 *
|| ||
|| (7)r8c5 - r8c1 = r9c2 - (7=3)r5c2 - (3=5)r3c2 - r3c5 = (5)r1c4 *
||
(3)r9c9 - (3=15)r7c78 *
=> -5 r7c4
Is that bidirectional? It sure is. You can start at any end point (assume it false) and one of the others will be forced. In other words, it works exactly like an AIC, except that it has multiple end points. The logic is easy to follow in a matrix as well:
5) 8x8 TM: Show
If one really wants (why?), it can also be turned into a contradiction net (Nishio):
6) Contradiction net:
- Code: Select all
----------------------------------------- (3)r9c2
/ ||
(5)r1c4 = r3c5 - (5=3)r3c2 - (3=7)r5c2 - r9c2 = r8c1 - (7)r8c5 ||
/ || ||
(5)r7c4 -------------------------------------------------------- (5)r8c5 ||
\ || ||
\ (3)r8c5 - (3)r9c4
\ ||
(5=13)r7c78 -------------------------------------------------- (3)r9c9
=> contradiction (3R9 empty) => -5 r7c4
Is that bidirectional? Of course. If you reverse it, it's the same kraken as before with the elimination included.
I wrote those examples quickly, so I don't guarantee that they're flawless.
Now, would someone have an actual example of a chain that isn't bidirectional?
-
SpAce - Posts: 2671
- Joined: 22 May 2017
Re: AIC and TDP
by SpAce » Fri Dec 27, 2019 2:08 am
Hi Robert,
False. Of course you can. Well, at least I can
Here's your net as a matrix (11x11 TM):
While that matrix flows more naturally from top to bottom, it can also be easily followed starting from the bottom (i.e. -4r9c2). It just has to go through three SIS with multiple members, which means lots of ORed branches making that direction more complicated. It could be written as a multi-kraken or an AIC-Net, both of which are bidirectional just like the matrix.
I already demonstrated that Phil's example is flawed. I'm pretty sure that the only reason why people think some chains are irreversible is because a) they write them incorrectly in the first place or b) they just don't know how to do read them backwards. In fact, reading any chain backwards is a great way to check that it doesn't have hidden errors.
Mauriès Robert wrote:The complex chains used with the TDP are generally not bidirectional. Here is an example with the puzzle below on which I plotted by a green color a complex chain obtained by assuming 6r1c2 false. The chain (see diagram) leads to 4r9c2 which eliminates 4r1c2. However, if you do -4r9c2, you can't go back up the chain.
False. Of course you can. Well, at least I can
original diagram: Show
Here's your net as a matrix (11x11 TM):
- Code: Select all
6r1c2 6r3c2
6r3c9 4r3c9
4r2c9 2r2c9
4r3c4 4r4c4
6r4c4 6r4c7
6r19c7 79r19c7
2r2c7 7r2c7 1r2c7
4r2c8 2r2c8 1r2c8 7r2c8
7r7c8 7r7c6
4r6c6 4r7c6 4r8c6
4r9c2 4r8c123
-----------------------------------------------------------------------
-4r1c2
While that matrix flows more naturally from top to bottom, it can also be easily followed starting from the bottom (i.e. -4r9c2). It just has to go through three SIS with multiple members, which means lots of ORed branches making that direction more complicated. It could be written as a multi-kraken or an AIC-Net, both of which are bidirectional just like the matrix.
Phil gives another example (http://www.philsfolly.net.au/chain_help.htm) but there are many others.
I already demonstrated that Phil's example is flawed. I'm pretty sure that the only reason why people think some chains are irreversible is because a) they write them incorrectly in the first place or b) they just don't know how to do read them backwards. In fact, reading any chain backwards is a great way to check that it doesn't have hidden errors.
-
SpAce - Posts: 2671
- Joined: 22 May 2017
Re: AIC and TDP
by Mauriès Robert » Fri Dec 27, 2019 5:41 pm
Hi SpAce and Eleven,
Reading what you write I understand that I'm not talking about the same things you're talking about.
When I say that a track (complex chain) is not bidirectional I mean this:
If (-A)->B->C->D->E we don't necessarily have (-E)->D->C->B->A, which is not at all the same as the reversibility described by Eleven.
So I apologize for this misunderstanding.
But even with Eleven's definition, in the example I give, it doesn't work.
Indeed, in my example we have:
(-6r1c2)->---- (see diagram) ---->(4r4c4 and 7r7c6)->4r8c6->4r9c2
Conversely we have (according to Eleven)
(-4r9c2)->-4r8c6->(-4r4c4 or -7r7c6) ...
If -4r4c4 is used to go up to 6r1c2, the same cannot be said of -7r7c6, I don't see how?
In any case, if the return from -4r9c2 to 6r1c2 is possible, it is not done by the same path as the one described for going from -6r1c2 to 4r9c2.
Robert
Reading what you write I understand that I'm not talking about the same things you're talking about.
When I say that a track (complex chain) is not bidirectional I mean this:
If (-A)->B->C->D->E we don't necessarily have (-E)->D->C->B->A, which is not at all the same as the reversibility described by Eleven.
So I apologize for this misunderstanding.
But even with Eleven's definition, in the example I give, it doesn't work.
Indeed, in my example we have:
(-6r1c2)->---- (see diagram) ---->(4r4c4 and 7r7c6)->4r8c6->4r9c2
- Code: Select all
- - - - - - - - - - - - - -
/ / \
-6r1c2->6r3c2->4r3c9->2r2c9- - - - - - - - ->1r2c7->7r2c8->7r7c6->4r8c6->4r9c2
\ / /
\ >6r4c7>79r19c7 /
\ / /
>4r4c4- - - - - - - - - - - - - - - - -
Conversely we have (according to Eleven)
(-4r9c2)->-4r8c6->(-4r4c4 or -7r7c6) ...
If -4r4c4 is used to go up to 6r1c2, the same cannot be said of -7r7c6, I don't see how?
In any case, if the return from -4r9c2 to 6r1c2 is possible, it is not done by the same path as the one described for going from -6r1c2 to 4r9c2.
Robert
- Mauriès Robert
- Posts: 603
- Joined: 07 November 2019
- Location: France
Re: AIC and TDP
by eleven » Fri Dec 27, 2019 6:14 pm
Mauriès Robert wrote:Conversely we have (according to Eleven)
(-4r9c2)->-4r8c6->(-4r4c4 or -7r7c6) ...
If -4r4c4 is used to go up to 6r1c2, the same cannot be said of -7r7c6, I don't see how?
Hi Robert,
i already told you in the other thread, that your net is incomplete.
Tell me, how 7r2c8 implies 7r7c6, and i will tell you, how -7r7c6 implies -7r2c8, and so on, for each implication.
The logic can never be wrong,
- eleven
- Posts: 3173
- Joined: 10 February 2008
Re: AIC and TDP
by Mauriès Robert » Fri Dec 27, 2019 6:27 pm
eleven wrote:i already told you in the other thread, that your net is incomplete.
Tell me, how 7r2c8 implies 7r7c6, and i will tell you, how -7r7c6 implies -7r2c8, and so on, for each implication.
The logic can never be wrong,
On r7, there are only 7r7c6 and 7r7c8. So 7r2c8 true => 7r7c8 false => 7r7c6 true.
Robert
Last edited by Mauriès Robert on Fri Dec 27, 2019 6:42 pm, edited 1 time in total.
- Mauriès Robert
- Posts: 603
- Joined: 07 November 2019
- Location: France
Re: AIC and TDP
by SpAce » Fri Dec 27, 2019 6:29 pm
Hi Robert,
It's not the same because it's incorrect. The reversal of the first chain is: -E -> -D -> -C -> -B -> A, like eleven explained. What other logical reversal could there be?
It does. Don't you trust my matrix?
So far so good.
The path for -7r7c6 is just more complicated. Follow my matrix from the bottom and you'll see. The only real problem is that your notation has so much less information, as I've said many times before. It makes it practically impossible to follow the chain (net) the other way. However, it's not impossible at all when it's expanded with the missing information, as in my matrix.
It's exactly the same path, but the logic is different because you have to consider several OR-branches. Look at the matrix.
Here's the logic drawn as an AIC-Net diagram, proving the derived strong link 4r9c2==6r1c2:
(Sorry, I don't have totuan's skills.) That's what it looks like if you follow the matrix from the bottom (I didn't even look at anything else when I drew this). Of course this is just as bidirectional as the other way -- all that's changed is the perspective. You can find the original logic by starting with the (6)r1c2 and following the chain to the left.
(Of course it would be much simpler to draw as a multi-kraken with the (1247)r2c8 as the main SIS, but that's not the point. It's just another perspective.)
Added. The same as an implication net:
Added 2. The same using negative implications that correspond with the original candidates:
Mauriès Robert wrote:If (-A)->B->C->D->E we don't necessarily have (-E)->D->C->B->A, which is not at all the same as the reversibility described by Eleven.
It's not the same because it's incorrect. The reversal of the first chain is: -E -> -D -> -C -> -B -> A, like eleven explained. What other logical reversal could there be?
But even with Eleven's definition, in the example I give, it doesn't work.
It does. Don't you trust my matrix?
Indeed, in my example we have:
(-6r1c2)->---- (see diagram) ---->(4r4c4 and 7r7c6)->4r8c6->4r9c2
...
Conversely we have (according to Eleven)
(-4r9c2)->-4r8c6->(-4r4c4 or -7r7c6) ...
So far so good.
If -4r4c4 is used to go up to 6r1c2, the same cannot be said of -7r7c6, I don't see how?
The path for -7r7c6 is just more complicated. Follow my matrix from the bottom and you'll see. The only real problem is that your notation has so much less information, as I've said many times before. It makes it practically impossible to follow the chain (net) the other way. However, it's not impossible at all when it's expanded with the missing information, as in my matrix.
In any case, if the return from -4r9c2 to 6r1c2 is possible, it is not done by the same path as the one described for going from -6r1c2 to 4r9c2.
It's exactly the same path, but the logic is different because you have to consider several OR-branches. Look at the matrix.
Here's the logic drawn as an AIC-Net diagram, proving the derived strong link 4r9c2==6r1c2:
- Code: Select all
(4)r9c2 *
||
(4)r8c123 - (4)r8c6
||
(4)r6c6 - r4c3 = r3c4 ------------ (4=6)r3c9 - r3c2 = (6)r1c2 *
|| / |
(4-7)r7c6 = r7c8 - (7)r2c8 / \ ---------- --------------------
|| / \ \
(4)r2c8 - | \
|| / \
(2)r2c8 -------------- (2=4)r2c9 \
|| / \
(1)r2c8 - (1)r2c7 / \
|| / \
(2)r2c7 - |
|| /
(7)r2c7 - (79=6)r19c7 - r4c7 = (6-4)r4c4 = (4)r3c4
(Sorry, I don't have totuan's skills.) That's what it looks like if you follow the matrix from the bottom (I didn't even look at anything else when I drew this). Of course this is just as bidirectional as the other way -- all that's changed is the perspective. You can find the original logic by starting with the (6)r1c2 and following the chain to the left.
(Of course it would be much simpler to draw as a multi-kraken with the (1247)r2c8 as the main SIS, but that's not the point. It's just another perspective.)
Added. The same as an implication net:
- Code: Select all
|4r9c2
|-4r9c2->|4r6c6->4r3c4---------------------------------------------------->6r3c9->6r1c2
|4r7c6->7r7c8->|4r2c8------------------------------------------>/
|2r2c8---------------------------------->4r2c9->/
|1r2c8->|2r2c7------------------------>/
|7r2c7->6r19c7->6r4c4->4r3c4->/
Added 2. The same using negative implications that correspond with the original candidates:
- Code: Select all
|4r9c2
|-4r9c2 -> -4r8c6 -> |-4r4c4 -----------------------------------------------------------> -4r3c9 -> -6r3c2 -> 6r1c2
|-7r7c6 -> -7r2c8 -> |-4r3c9-------------------------------------->/
|-2r2c9 -> --------------------------------->/
|-1r2c7 -> |-2r2c9 ------------------------>/
|-79r19c7 -> -6r4c7 -> -4r4c4 ->/
Last edited by SpAce on Fri Dec 27, 2019 8:01 pm, edited 2 times in total.
-
SpAce - Posts: 2671
- Joined: 22 May 2017
Re: AIC and TDP
by eleven » Fri Dec 27, 2019 7:01 pm
Ok, so reverse it withMauriès Robert wrote:On r7, there are only 7r7c6 and 7r7c8. So 7r2c8 true => 7r7c8 false => 7r7c6 true.
Robert
-7r7c6 (-> 7r7c8) -> -7r2c8
Next step is
- Code: Select all
4r3c9 ->
\ (and)
1r2c7 -> 7r2c8
Is it 4r3c9 -> 7r3c4 -> 4r2c5 AND 1r2c7, so 7r2c8 is the last in the row ?
In this case the reverse is
- Code: Select all
(7r2c5 -> -4r2c5 -> -7r3c4 -> 4r3c4) -> -4r3c9
/ (or)
-7r2c8 -> 7r2c7 -> -1r2c7
- eleven
- Posts: 3173
- Joined: 10 February 2008
Re: AIC and TDP
by Mauriès Robert » Fri Dec 27, 2019 7:20 pm
eleven wrote:What is your logic ?
Is it 4r3c9 -> 7r3c4 -> 4r2c5 AND 1r2c7, so 7r2c8 is the last in the row ?
No, in my diagram, the logic is: (4r3c9 and 2r2c9 and 1r2c7)->7r2c8
Robert
- Mauriès Robert
- Posts: 603
- Joined: 07 November 2019
- Location: France
Re: AIC and TDP
by SpAce » Fri Dec 27, 2019 7:23 pm
eleven wrote:Is it 4r3c9 -> 7r3c4 -> 4r2c5 AND 1r2c7, so 7r2c8 is the last in the row ?
I thought it was the last in the cell.
-
SpAce - Posts: 2671
- Joined: 22 May 2017
Re: AIC and TDP
by Mauriès Robert » Fri Dec 27, 2019 8:12 pm
Hi SpAce,
Thank you for your many explanations and the diagrams below very readable for me.
So I was wrong!
Robert
Thank you for your many explanations and the diagrams below very readable for me.
- Code: Select all
|4r9c2
|-4r9c2->|4r6c6->4r3c4---------------------------------------------------->6r3c9->6r1c2
|4r7c6->7r7c8->|4r2c8------------------------------------------>/
|2r2c8---------------------------------->4r2c9->/
|1r2c8->|2r2c7------------------------>/
|7r2c7->6r19c7->6r4c4->4r3c4->/
- Code: Select all
|4r9c2
|-4r9c2 -> -4r8c6 -> |-4r4c4 -----------------------------------------------------------> -4r3c9 -> -6r3c2 -> 6r1c2
|-7r7c6 -> -7r2c8 -> |-4r3c9-------------------------------------->/
|-2r2c9 -> --------------------------------->/
|-1r2c7 -> |-2r2c9 ------------------------>/
|-79r19c7 -> -6r4c7 -> -4r4c4 ->/
So I was wrong!
Robert
- Mauriès Robert
- Posts: 603
- Joined: 07 November 2019
- Location: France
Re: AIC and TDP
by eleven » Fri Dec 27, 2019 10:00 pm
Mauriès Robert wrote:No, in my diagram, the logic is: (4r3c9 and 2r2c9 and 1r2c7)->7r2c8
Robert
Ah, i missed that slash, sorry.
So let's turn the whole net around.
- Code: Select all
- - - - - - - - - - - - - -
/ / \
-6r1c2->6r3c2->4r3c9->2r2c9- - - - - - - - ->1r2c7->7r2c8->7r7c6->4r8c6->4r9c2
\ / /
\ >6r4c7>79r19c7 /
\ / /
>4r4c4- - - - - - - - - - - - - - - - -
Now read from right to left:
- Code: Select all
...or.....................or.......
/ / \or
6r1c2<= -6r3c2<= -4r3c9 <= .............. -2r2c9 <= -1r2c7 <= -7r2c8 <= -7r7c6 <= -4r8c6 <= -4r9c2
\ / or /
\ <= -6r4c7 <= -79r19c7 / or
\ / /
<= -4r4c4 ...........................................
- eleven
- Posts: 3173
- Joined: 10 February 2008
41 posts
• Page 2 of 3 • 1, 2, 3
