The New Sudoku Players' Forum

[Wecoc]

This sudoku technique is based on coloring and chains, but targets a very specific situation fairly easy to spot, both by humans and computers.
These are my personal thoughts on this technique, but first I will shortly explain what it is (you can watch the videos for extended explanation)

How it works

What we are looking for is a number that is solved (or given) at least once in every band and in a different stick for each band.

Once we detect a number that follows that restriction, we mark its possible positions in the other 'unsolved' blocks. Then, we pick a block and test in each possible cell which ones clash. It doesn't matter which block you pick to start with, the final conclusion is pretty much the same with a few exceptions I'll say below. Despite that, blocks with only 2 possible cells for that candidate will mean less chains to check, therefore better performance for the solver.

In case one of the possibilities clash (you reach a contradiction), you can directly eliminate it as candidate in that cell. In the other hand, if all possibilities don't clash there may be some positions in other blocks that can't contain the number in any case (aren't included in any chain), therefore you can eliminate the candidate in those cells.

Finally if there are too many possibilities in some blocks the chains may be not useful at all.

Exceptions on the "start with 2" rule

Start with 2: We will start with a block with 2 possibilities for that number, to compare the chains in each case.

When there's one block with 4 possibilities or more, you should always start with that one, to try to reduce some of the candidates.
When there's more than one block with 4 possibilities or more, almost always the technique will be useless until you fill enough numbers in the grid to remove some of those candidates.
When there aren't blocks with 4 possibilities and the chains still get stuck, you start again the slot machine on the block where the chains got stuck independently on how many possibilities it has.

Video instructions and examples

A Brand New Trick For Very Hard Sudoku Puzzles - Introduction
The Easy Way To Spot X-Cycles - Example puzzle #1
Using the Brain(ium) Power - Example puzzle #2
More Brand New Sudoku Logic: Linked Slot Machines - Advanced alternatives of the technique

When should we apply the Slot Machine

This technique was thought for being used by human solvers on very hard sudokus, but the interesting question here is whether or not it could improve performance on computer solvers.
Can we apply this in an algorithm in an efficient, trustable and falsifiable manner? How can we achieve that?

Picking the starting point

As I said we will prioritize blocks with only 2 possible cells for that number except for the mentioned exceptions, but there may be more than one. Which one should we pick?

We need to pick one in a non-random way that arrives to the same conclusion between isomorphs (rotation/translation).
To do that we need to either:
- Demonstrate every 2-candidates block has the exact same conclusion
- If that's not possible, elaborate a 'which block next' algorithm to find the better one in each case

It would be useful to have a way to verify beforehand if the technique will reach to something we can use, so the solver discards the technique without having to check any chain in the worse cases.
We could deduce this either counting the number of candidates in each block, or more probably looking at the shapes they form.

Finally, the easiest way to find which number should we look for is checking the starting restriction in each one, sorted. Sadly, that can produce unwanted differences between isomorphs (made by swapping the givens), a better way to pick the more useful number would also benefit the solver.

[StrmCkr]

Slot machine
Is
Simple colouring ie x-cycle
Single digit Muti colouring ie x-cycles
Muti colouring /3d Medusa (some overlapping muti fish)
Which is just fish logic. N digits In N cells

Nothing new here

[Wecoc]

Slot machine is Simple colouring ie x-cycle

That's what I first thought too, and I kind of agree, but I fail to explain why algorithms that apply coloring and X-Cycles usually don't find the same chains explained in the examples, and have to go further more steps and more 'diabolical' techniques in order to progress. That's why I suggested comparing algorithms that include this case with those only using the default coloring.
Even if it really is just a specific case of coloring/fishy cycle, maybe that specific case is being under-represented by the solvers. Either that or there is something more obscure going on behind this logic

[SpAce]

Slot machine is Simple colouring ie x-cycle

That's what I first thought too, and I kind of agree, but I fail to explain why algorithms that apply coloring and X-Cycles usually don't find the same chains explained in the examples, and have to go further more steps and more 'diabolical' techniques in order to progress. That's why I suggested comparing algorithms that include this case with those only using the default coloring.
Even if it really is just a specific case of coloring/fishy cycle, maybe that specific case is being under-represented by the solvers. Either that or there is something more obscure going on behind this logic

I doubt it. You'd have to provide examples (not on videos) before I believe it's anything but a spotting aid for potential X-Chains (easy enough anyway). Then again, I only looked at part of the first video (ridiculously titled about "very hard puzzles") so I might not have a complete understanding of the technique -- and in that case I never will unless there's a comprehensive textual explanation (including examples) somewhere. I refuse to waste my time on slow-paced videos when I could read the same information in a minute and probably conclude that there was nothing new and interesting.

[qiuyanzhe]

I didn't understand it completely, and due to some limitations I cannot watch the videos. So here are some of my ideas:
'Slot Machine' means a solving method on a single digit, that works mainly when three of it are given in boxes like Boxes 1,5 and 9.
When all possible places in a box form an intersection, this would not work on that digit.
When all possible places in a box are two cells diagonally(2), it would be more likely to work.
When 3 of the cells are possible(3), it is a restriction similar to “a OR b is TRUE”
If there is a box with all places possible(4), no cells in another box can be eliminated.
If there is a 4, start with a 3 and see if there is a conclusion in the 4-box.

Code: Select all

..|o.|o.
..|.o|.o
––+––+––
o.|..|.o
.o|..|oo
––+––+––
oo|o.|..
oo|.o|..


r1c5 OR r3c1 is TRUE
r5c3 OR r3c1 is TRUE
ELIMINATE r5c1

Hidden Text: Show

And all chain-like things there could be are:

Code: Select all

#swordfish
..|oo|oo
..|.o|.o
––+––+––
o.|..|.o
.o|..|oo
––+––+––
xo|oo|..
o.|.o|..


Code: Select all

#SE 6.7 chains(col35 box4)
..|oo|oo
..|.o|.o
––+––+––
o.|..|.o
.o|..|oo
––+––+––
xo|oo|..
oo|.o|..


Code: Select all

#More. Finned Swordfish, or chain on r23 and c3, still SE6.7
..|oo|oo
..|.o|.o
––+––+––
o.|..|.o
oo|..|oo
––+––+––
xo|oo|..
oo|.o|..


Similarly, if.the 4 in the examples above is a 3, we may have the digit finished. I have made many such puzzles several years ago,haha

[StrmCkr]

Depends which solver your using scan raids solver isn't able to do full views of potential examples at each state compared to say hoduku.

Add to this the fact scan raids algorthiumms for techniques are not fully comprehensive and miss stuff frequently if they fall under another named technique higher up in its search order.

At best the advanced chains are 3d mesdsa ie advanced Muti colouring.
(as the example quin shown 3 way bilocal intersections found by colouringl

So really nothing new.

[SpAce]

Despite my promise I suffered through half of the last video about the linked slot machines, because it seemed most likely to contain something new. It didn't. Unless I'm still missing something important, my conclusion at this point is:

• Basic Slot Machine: may help to spot some single-digit chains/fishes.
• Linked Slot Machine: may help to spot some multi-digit chains/fishes.

So, it's a spotting aid for existing and well-known elimination techniques, and may be somewhat useful as such especially if solving without candidates, but doesn't really provide any new solving power. I don't think anyone who's good at advanced coloring or finding chains otherwise really benefits from it. As a spotting aid it seems less useful than keith's technique for finding single-digit eliminations.

I actually use my adaptation of keith's technique a lot especially when solving without pencil marks, because it's extremely quick to see whether a digit has any chain/fish potential at all, reducing the number of checks needed. One difference between the two is that keith's technique has definite coverage, but the Slot Machine doesn't (it's just a heuristic). You can see that if you look at keith's examples -- as far as I understand, the slot machine wouldn't find those Skyscrapers because the givens are in a single stack.

At best the advanced chains are 3d mesdsa ie advanced Muti colouring.

That's not entirely correct. 3D Medusa covers a small subset of multi-digit AICs, just like Simple Coloring covers only a small subset of X-Chains, because both only use conjugate links. The slot machine seems to find more advanced chains than those because it can cross weak-only links and use group nodes, but it doesn't find them all. Truly advanced coloring techniques like GEM or full tagging do, so I don't really see why I'd limit myself to something less powerful and not much simpler to use.

So really nothing new.

I agree -- unless someone demonstrates that we've missed something.

----

Slot machine is Simple colouring ie x-cycle

That's what I first thought too, and I kind of agree, but I fail to explain why algorithms that apply coloring and X-Cycles usually don't find the same chains explained in the examples, and have to go further more steps and more 'diabolical' techniques in order to progress.

It happens if you look at the Linked Slot Machine examples, because it finds multi-digit chains (which by definition can't be found as X-Chains -- they're generic AICs or sometimes XY-Chains). The basic slot machine is limited to X-Chains, however. As StrmCkr also explained, the SudokuWiki solver is a poor choice to test this because it can only show one kind of each technique at a time (and not always the best one). Use something like Hodoku if you want to see what patterns are actually available. I bet that the X-Chains it finds are a superset of those found found by the basic Slot Machine, and the same with its AICs vs the Linked Slot Machine.

[SpAce]

Here's an example taken from today's puzzle. The puzzle contains several X-Chains and fishes (all for one digit, though). Does the basic Slot Machine suggest their existence and help you find them? I don't see how. On the other hand, keith's technique tells me almost instantly what digits and in what boxes are worth looking at.

The pencil marks after basics:

Code: Select all

.-----------------.------------.---------------.
| 4      8    6   | 7   9   3  | 2    5   1    |
| 9      37   2   | 8   5   1  | 367  4   367  |
| 137    5    137 | 6   4   2  | 379  8   379  |
:-----------------+------------+---------------:
| 35678  367  357 | 4   26  57 | 1    9   2368 |
| 156    2    15  | 9   3   8  | 56   7   4    |
| 3578   9    4   | 1   26  57 | 35   26  38   |
:-----------------+------------+---------------:
| 256    1    59  | 25  8   4  | 679  3   2679 |
| 267    4    79  | 3   1   69 | 8    26  5    |
| 2356   36   8   | 25  7   69 | 4    1   269  |
'-----------------'------------'---------------'


With (or without) any form of digit filtering it's easy to see with keith's simple rules that digits {1 2 4 5 7 8 9} can't have any single-digit eliminations (via X-Chains or fishes) available, and no further solving can change that. It's a final result so we can completely exclude those digits from any further consideration for such techniques. It takes me about a second per digit to see that, so it's a very efficient way to reduce single-digit checks. In this case it leaves only 3 and 6 to need further checking.

The 3s could have something in boxes 1,3,4,6 but there aren't useful strong links or fish formations there, so we can forget it for now. Seeing that quickly isn't quite as easy or certain, as some grouped links or complex fishes may be easy to miss, but in this case there's nothing to miss (further eliminations of 3s can change that, though, so we might need to recheck them later). So, we only have digit 6 left to check at this time:

Code: Select all

.--------------------.---------------.------------------.
|  4       8    <6>  |  7    9    3  |  2     5    1    |
|  9       37    2   |  8    5    1  | *367   4   *367  |
|  137     5     137 | <6>   4    2  |  379   8    379  |
:--------------------+---------------+------------------:
| *35678  *367   357 |  4   *26   57 |  1     9   *2368 |
| *156     2     15  |  9    3    8  | *56    7    4    |
|  3578    9     4   |  1   *26   57 |  35   *26   38   |
:--------------------+---------------+------------------:
| *256     1     59  |  25   8    4  | *679   3   *2679 |
| *267     4     79  |  3    1   *69 |  8    *26   5    |
| *2356   *36    8   |  25   7   *69 |  4     1   *269  |
'--------------------'---------------'------------------'

Does the Slot Machine tell you anything about those 6s? I don't think so, because the only solved 6s (givens actually) are in boxes 1 and 2, so it doesn't fit the pattern. Yet there's a lot of X-Chain/fish potential, and I can see that instantly with keith's technique -- as well as the fact that the elimination potential is limited to boxes 4,6,7,9. From there it's easy to find a number of different X-Chains/Loops or fishes just by looking at the candidate patterns or using coloring if needed. (I wouldn't use any of them to solve this puzzle though, but that's not the point here.)

Available single-digit eliminations: Show

Some patterns that would get all five of the available single-digit eliminations at once:

X-Loop: (6)r9c2 = r4c2 - r4c5 = r6c5 - r6c8 = r8c8 - r8c6 = (6)r9c6 - loop => -6 r4c19,r8c1,r9c19
Jellyfish 6:c2568\r4689 => -6 r4c19,r8c1,r9c19
Swordfish 6:r257\c179 => -6 r489c1,r49c9

Code: Select all

.---------------------.---------------.-------------------.
|  4        8    <6>  |  7    9    3  |  2     5    1     |
|  9        37    2   |  8    5    1  | *367   4   *367   |
|  137      5     137 | <6>   4    2  |  379   8    379   |
:---------------------+---------------+-------------------:
| *3578-6  *367   357 |  4   *26   57 |  1     9   *238-6 |
| *156      2     15  |  9    3    8  | *56    7    4     |
|  3578     9     4   |  1   *26   57 |  35   *26   38    |
:---------------------+---------------+-------------------:
| *256      1     59  |  25   8    4  | *679   3   *2679  |
| *27-6     4     79  |  3    1   *69 |  8    *26   5     |
| *235-6   *36    8   |  25   7   *69 |  4     1   *29-6  |
'---------------------'---------------'-------------------'

There are also many other single-digit patterns available that would get only some of those eliminations at a time.

So, unless you can show me that the Slot Machine would somehow find those same (or any) X-Chains/fishes (or their eliminations) here, I'm about ready to deem it completely useless as it's obviously limited to some special cases only.

[StrmCkr]

Code: Select all

.-------------------.---------------------.-------------------.
| 489   5789  45789 | 2      35679  3567  | 1     3789  3467  |
| 1289  3     1789  | 19     4      167   | 6789  5     267   |
| 1249  2579  6     | 1359   3579   8     | 479   2379  2347  |
:-------------------+---------------------+-------------------:
| 5     689   1389  | 7      368    346   | 2     139   134   |
| 2369  4     379   | 35     1      2356  | 579   379   8     |
| 1238  278   1378  | 3458   2358   9     | 457   6     13457 |
:-------------------+---------------------+-------------------:
| 4689  1     4589  | 4589   25789  2457  | 3     278   2567  |
| 7     5689  3589  | 13589  23589  1235  | 568   4     1256  |
| 348   58    2     | 6      3578   13457 | 578   178   9     |
'-------------------'---------------------'-------------------'

First example: from the video
Finned Swordfish: 2 r258 c169 fr8c5 => r7c6<>2
or
X-Chain: 2 r5c6 =2= r5c1 -2- r2c1 =2= r2c9 -2- r3c8 =2= r7c8 => r7c6<>2
or
Discontinuous Nice Loop: 2 r7c6 -2- r7c8 =2= r3c8 -2- r3c2 =2= r6c2 -2- r6c5 =2= r5c6 -2- r7c6 => r7c6<>2

2nd example: from the same state above:
Finned Swordfish: 4 r149 c169 fr1c3 => r3c1<>4
Finned Swordfish: 4 r349 c169 fr3c7 => r1c9<>4
Finned Mutant Squirmbag: 4 r49c347 r67c169 fr1c3 fr3c7 => r1c9,r3c1<>4
Multi Colors 1: 4 (r1c3) / (r7c3), (r4c6,r7c4) / (r4c9,r6c4) => r1c9<>4
X-Chain: 4 r1c3 =4= r7c3 -4- r7c4 =4= r6c4 -4- r6c7 =4= r3c7 => r1c9,r3c1<>4
X-Chain: 4 r1c3 =4= r7c3 -4- r7c4 =4= r6c4 -4- r4c6 =4= r4c9 => r1c9<>4
X-Chain: 4 r3c7 =4= r6c7 -4- r6c4 =4= r7c4 -4- r9c6 =4= r9c1 => r3c1<>4
AIC: 4 4- r1c3 =4= r7c3 -4- r7c4 =4= r6c4 -4- r6c7 =4= r3c7 -4 => r1c9,r3c1<>4
Discontinuous Nice Loop: 4 r1c9 -4- r1c3 =4= r7c3 -4- r7c4 =4= r6c4 -4- r6c7 =4= r3c7 -4- r1c9 => r1c9<>4
Discontinuous Nice Loop: 4 r3c1 -4- r3c7 =4= r6c7 -4- r6c4 =4= r7c4 -4- r7c3 =4= r1c3 -4- r3c1 => r3c1<>4

3rd example:
Finned Swordfish: 6 r157 c169 fr1c5 => r2c6<>6
Finned Swordfish: 6 r257 c169 fr2c7 => r1c9<>6
Finned Mutant Squirmbag: 6 r57c257 r48c169 fr1c5 fr2c7 => r1c9,r2c6<>6
Multi Colors 1: 6 (r1c5) / (r4c5), (r4c2,r5c6,r7c1) / (r5c1,r7c9,r8c2) => r1c9<>6
Multi Colors 1: 6 (r4c2,r5c6,r7c1) / (r5c1,r7c9,r8c2), (r2c7) / (r8c7) => r2c6<>6
X-Chain: 6 r1c5 =6= r4c5 -6- r4c2 =6= r8c2 -6- r8c7 =6= r2c7 => r1c9,r2c6<>6
X-Chain: 6 r1c5 =6= r4c5 -6- r4c2 =6= r8c2 -6- r7c1 =6= r7c9 => r1c9<>6
X-Chain: 6 r2c7 =6= r8c7 -6- r8c2 =6= r4c2 -6- r5c1 =6= r5c6 => r2c6<>6
AIC: 6 6- r1c5 =6= r4c5 -6- r4c2 =6= r8c2 -6- r8c7 =6= r2c7 -6 => r1c9,r2c6<>6
Discontinuous Nice Loop: 6 r1c9 -6- r1c5 =6= r4c5 -6- r4c2 =6= r8c2 -6- r8c7 =6= r2c7 -6- r1c9 => r1c9<>6
Discontinuous Nice Loop: 6 r2c6 -6- r2c7 =6= r8c7 -6- r8c2 =6= r4c2 -6- r4c5 =6= r1c5 -6- r2c6 => r2c6<>6


then it goes into linked slot machine:
4th example:
AIC: 2/6 2- r2c9 =2= r2c1 -2- r5c1 -6- r7c1 =6= r7c9 -6 => r7c9<>2, r2c9<>6
AIC: 6 6- r2c7 =6= r2c9 =2= r2c1 -2- r5c1 -6- r7c1 =6= r7c9 -6 => r2c9,r8c7<>6

then says there is a forcing network ..... lol which removes a "4" at R3C9
{which is a small backdoor}
with out a diagram for that my conclusion from here out is that this is a true/false network based on coloring mechanics and still nothing new. {multi coloring/3d medusa } fishies, xcycles, muti-fish very limited version.

as the rest of the examples are basically the same examples as the previous 4 examples which are explained using shorter logic.

but his slot machine does miss the "5" eliminations before he makes a mess following andreils thread.

Code: Select all

.------------------.--------------------.------------------.
| 49    579   4579 | 2     35679  3567  | 1    8     37    |
| 1289  3     1789 | 19    4      17    | 6    5     27    |
| 12    257   6    | 135   357    8     | 479  2379  2347  |
:------------------+--------------------+------------------:
| 5     689   1389 | 7     368    346   | 2    139   134   |
| 26    4     379  | 35    1      26    | 579  379   8     |
| 1238  278   1378 | 3458  2358   9     | 457  6     13457 |
:------------------+--------------------+------------------:
| 4689  1     4589 | 489   25789  457   | 3    27     567  |
| 7     5689  3589 | 1389  23589  1235  | 58   4     1256  |
| 348   58    2    | 6     3578   13457 | 578  17    9     |
'------------------'--------------------'------------------'

Finned Franken Jellyfish: 5 r359b5 c2457 fr9c6 efr5c4 => r78c4<>5

[Wecoc]

with out a diagram for that my conclusion from here out is that this is a true/false network based on coloring mechanics and still nothing new. {multi coloring/3d medusa } fishies, xcycles, muti-fish very limited version.

This quote on the last video talks about it. I don't think it's exactly SC, it's more of another way to detect and think about some of those chains.

It's different from Simple Coloring in that in SC you are looking at binary states (whether something can be ON or OFF, and you have 2 colors for those), here I'm just trying to keep track on chains with individual numbers by highlighting what color those individual numbers are.

Anyways what I wanted to test was if using this there was possible room for optimization on the algorithms or not (it was improbable but it was worth a shot), even if it really is just another fancy way to spot X-Chains.
As far as I tried, this sometimes finds Swordfish, Finned Swordfish, Nishio Forcing Chains or more exotic things, so it's not a trick focused on a very specific type of chain, but it also doesn't find them all nor is always applicable, so it would be complementary on the keith's technique, not a substitution.

I found one case where the solvers and this technique follow different "solving paths". Both paths seem to be equally short.

This is the last example on the first video:

Code: Select all

3..9..7...8...4.2.....5...19....86...2.3...5...1.......6..7..4......29....51.....

Code: Select all

+----------------------------------------------------------+
|     3   15   246 |     9    28   16 |     7    68   4568 |
|    15    8   679 |    67   136    4 |    35     2   3569 |
|  2467  479 24679 |    28     5  367 |   348  3689      1 |
+----------------------------------------------------------+
|     9 3457   347 |  2457   124    8 |     6   137   2347 |
|  4678    2  4678 |     3  1469 1679 |   148     5   4789 |
| 45678 3457     1 | 24567  2469 5679 |  2348  3789 234789 |
+----------------------------------------------------------+
|   128    6  2389 |    58     7  359 | 12358     4   2358 |
|  1478 1347  3478 |  4568  3468    2 |     9 13678  35678 |
|  2478 3479     5 |     1 34689  369 |   238  3678  23678 |
+----------------------------------------------------------+

Hodoku v2.2.0 doesn't find anything using 1s there, but solves it using a Swordfish with 5s:
Swordfish: 5 r148 c249 => r27c9,r6c24,r7c4<>5; stte

The Slot Machine on 5s arrives to exactly the same conclusion, but you could also apply it on 1s, which allows to remove 1 as candidate in r4c5 and place 1 in r3c9,r7c7; stte

I suspect if there wasn't a Swordfish on 5s the solver would automatically find the alternative path.

I also tried the trick on some of the Weekly Unsolvable, but as expected it didn't find anything useful.

[SpAce]

I found one case where the solvers and this technique follow different "solving paths". Both paths seem to be equally short.

This is the last example on the first video:

Code: Select all

3..9..7...8...4.2.....5...19....86...2.3...5...1.......6..7..4......29....51.....

Hodoku v2.2.0 doesn't find anything using 1s there, but solves it using a Swordfish with 5s:
Swordfish: 5 r148 c249 => r27c9,r6c24,r7c4<>5; stte

The Slot Machine on 5s arrives to exactly the same conclusion, but you could also apply it on 1s, which allows to remove 1 as candidate in r4c5 and place 1 in r3c9,r7c7; stte

What are you talking about? Hodoku finds pages of chains and fishes with the 1s, of course. If single-digit eliminations are available it almost certainly finds them all, and it can also list pretty much every possible chain or fish type explaining them (plus optionally those that are only available through templates and not chains or fishes).

I seriously doubt there's any valid elimination that any version of the Slot Machine finds that Hodoku doesn't, but certainly not when it comes to single-digit eliminations. I guess you're just not using it properly, if you end up with a different conclusion.

[SpAce]

Code: Select all

.-------------------.---------------------.-------------------.
| 489   5789  45789 | 2      35679  3567  | 1     3789  3467  |
| 1289  3     1789  | 19     4      167   | 6789  5     267   |
| 1249  2579  6     | 1359   3579   8     | 479   2379  2347  |
:-------------------+---------------------+-------------------:
| 5     689   1389  | 7      368    346   | 2     139   134   |
| 2369  4     379   | 35     1      2356  | 579   379   8     |
| 1238  278   1378  | 3458   2358   9     | 457   6     13457 |
:-------------------+---------------------+-------------------:
| 4689  1     4589  | 4589   25789  2457  | 3     278   2567  |
| 7     5689  3589  | 13589  23589  1235  | 568   4     1256  |
| 348   58    2     | 6      3578   13457 | 578   178   9     |
'-------------------'---------------------'-------------------'

First example: from the video

Here's my manual solution for that. I haven't tried to optimize or analyze it at all, so it's just the raw steps I took when solving. Some are pretty ugly, but they did the job. Of course I found other eliminations as well, but didn't end up needing them. It took 12 steps which seemed awfully lot, especially since they're not the simplest kinds. For some reason I didn't figure out a good strategy for this, so I ended up just killing enough more or less random candidates to find an opening. So, it's probably not very efficient at all. With my settings Hodoku used 22 steps by default (but it could do it in just two).

Code: Select all

...2..1...3..4..5...6..8...5..7..2...4..1...8.....9.6..1....3..7......4...26....9 (SE 8.9)

Step 1: -2 r7c9, -6 r12c9: Show

After basics (1 HP):

Code: Select all

.---------------------.------------------------.-----------------------.
|   489   5789  45789 | 2      f35(6)79  3567  | 1     3789    347-6   |
|  e1289  3     1789  | 19      4        167   | 6789  5     f(2)7-6   |
|   1249  2579  6     | 1359    3579     8     | 479   2379    2347    |
:---------------------+------------------------+-----------------------:
|   5    d689   1389  | 7      e368      346   | 2     139     134     |
| cd26    4     379   | 35      1        26    | 579   379     8       |
|   1238  278   1378  | 3458    2358     9     | 457   6       13457   |
:---------------------+------------------------+-----------------------:
|  b4689  1     4589  | 4589    25789    2457  | 3     278    a5[6]7-2 |
|   7     5689  3589  | 13589   23589    1235  | 568   4       1256    |
|   348   58    2     | 6       3578     13457 | 578   178     9       |
'---------------------'------------------------'-----------------------'

Step 1: (6)r7c9 = r7c1 - r5c1 = (26)b4p42 - (2|6)r2c1,r4c5 = (2)r2c9&(6)r1c5 => -2 r7c9, -6 r12c9

(2 placements)

Steps 2-4: -2 r7c6, -58 r8c2, -4 r1c9,r3c1: Show

Code: Select all

.----------------------------.------------------------.----------------------.
|   49       579     o[4]579 |  2      35679    3567  |   1      8     37-4  |
|   1289     3         1789  |  19     4        17    |   6      5     27    |
|   12-4    d257       6     |  135    357      8     | t(4)79  e2379  2347  |
:----------------------------+------------------------+----------------------:
|   5       B689      B1389  |  7      368      346   |   2      139   134   |
|  b26       4        B379   |  35     1      a[2]6   |   579    379   8     |
|   1238    c278       1378  | r3458   2358     9     |  s457    6     13457 |
:----------------------------+------------------------+----------------------:
| BC4689     1       Cp4589  | q4589   25789    457-2 |   3    f(2)7   567   |
|   7     AD[69]-58   C3589  |  13589  23589    1235  |   58     4     1256  |
|   348      58        2     |  6      3578     13457 |   578    17    9     |
'----------------------------'------------------------'----------------------'

Step 2: (2)r5c6 = r5c1 - r6c2 = r3c2 - r3c8 = (2)r7c8 => -2 r7c6

Step 3: (6)r8c2 = (6)r7c1&(69)b4p236 - (9)b7p136 = (9)r8c2 => -58 r8c2

Step 4: (4)r1c3 = r7c3 - r7c4 = r6c4 - r6c7 = (4)r3c7 => -4 r1c9,r3c1

Step 5: -3 r6c49, -5 r7c4: Show

Code: Select all

.--------------------.-------------------------.-----------------------.
|  49      579  4579 |  2        35679   3567  |  1     8     g(3)7    |
|  1289    3    1789 |  19       4       17    |  6     5       27     |
|  12      257  6    |  135      357     8     | f479  f2379  g(3)247  |
:--------------------+-------------------------+-----------------------:
|  5       689  1389 |  7        368     346   |  2     139     134    |
|  26      4    379  | g3(5)     1       26    | f579   379     8      |
| a12[3]8  278  1378 | d(4)58-3  2358    9     | e457   6       1457-3 |
:--------------------+-------------------------+-----------------------:
|  4689    1    4589 | c[4]89-5  25789   457   |  3     27      567    |
|  7       69   3589 |  13589    23589   1235  |  58    4       1256   |
| b348     58   2    |  6        3578   b13457 |  578   17      9      |
'--------------------'-------------------------'-----------------------'

Step 5: (3)r6c1 = (3,4)r9c16 - @(4)r7c4 = (4)r6c4@ - r6c7 = (49-3|5)r3c78,r5c7 = (3)r13c9&(5)r5c4 => -3 r6c49, -5 r7c4

Step 6: -8 r7c3,r89c5: Show

Code: Select all

.----------------------.-----------------------.-------------------.
| 49    d579   e4579   |  2      35679   3567  |  1     8     37   |
| 1289   3      1789   |  19     4       17    |  6     5     27   |
| 12    d257    6      |  135    357     8     |  479   2379  2347 |
:----------------------+-----------------------+-------------------:
| 5      689    1389   |  7     g36(8)   346   |  2     139   134  |
| 26     4      379    |  35     1       26    |  579   379   8    |
| 1238   278    1378   | g458   g235(8)  9     |  457   6     1457 |
:----------------------+-----------------------+-------------------:
| 4689   1    e(4)59-8 | f489    25789   457   |  3     27    567  |
| 7      69     3589   |  13589  2359-8  1235  | a5[8]  4     1256 |
| 348   c5[8]   2      |  6      357-8   13457 | b578   17    9    |
'----------------------'-----------------------'-------------------'

Step 6: (8)r8c7 = r9c7 - @(8=5)r9c2 - r13c2 = (5,4)r17c3@ - r7c4 = (48)b5p728 => -8 r7c3,r89c5

Step 7: -1 r9c6: Show

Code: Select all

.-------------------------.-------------------------.--------------------.
|   ai49     iL57+9  4579 | 2      35679   3567     | 1      8      37   |
|  hiL12+89    3     1789 | 19     4       17       | 6      5      27   |
|    L12      L257   6    | 135    357     8        | 479    2379   2347 |
:-------------------------+-------------------------+--------------------:
|     5        689   1389 | 7      368     346      | 2      139    134  |
|     26       4     379  | 35     1       26       | 579    379    8    |
|     1238     278   1378 | 458    2358    9        | 457    6      1457 |
:-------------------------+-------------------------+--------------------:
| aDgN49+68    1     459  | 489    25789   457      | 3      27    E567  |
|     7        69    3589 | 13589  2359    1235     | 58     4     F1256 |
|   bj348     M58    2    | 6      357   ck3[4]57-1 | 578  F(1)7    9    |
'-------------------------'-------------------------'--------------------'

Step 7: Double Kraken AALS(49+68)r17c1, AALS(1257+89)b1p2478

Code: Select all

(94)r17c1 - r9c1 = (4)r9c6
||
(6)r7c1 - r7c9 = (61)b9p68
||
(8)r7c1 - (8)r2c1
          ||
          (94)b1p241 - r9c1 = (4)r9c6
          ||
          (1275)b1p4728 - (5=8)r9c2 - r7c1 ... = (4)r9c6|(61)b9p68

=> -1 r9c6 (1 placement)

Step 8: -5 r7c9: Show

Code: Select all

.----------------------.---------------------.--------------------.
| h49      579  h4579  |  2     f35679  3567 | 1    8       37    |
| g1289    3     1789  | f19     4      17   | 6    5       27    |
|  12      257   6     |  135    357    8    | 479  2379    2347  |
:----------------------+---------------------+--------------------:
|  5      d689   1389  |  7     e368    346  | 2    39      134   |
|  26      4     379   |  35     1      26   | 579  379     8     |
|  1238    278   1378  |  458    2358   9    | 457  6       1457  |
:----------------------+---------------------+--------------------:
| g4689    1    i4(5)9 |  489    25789  457  | 3    27    a[6]7-5 |
|  7     cd69    3589  |  13589  2359   1235 | 58   4      b256   |
|  348     58    2     |  6      357    3457 | 578  1       9     |
'----------------------'---------------------'--------------------'

Step 8: (6)r7c9 = r8c9 - r8c2 = (9*6)r84c2 - r4c5 = (69)b2p24 - r2*7c1 = (9,4)r1c13 - (4|*9=5)r7c3 => -5 r7c9

Step 9: -1 r6c1, -3 r4c36, -5 r8c3: Show

Code: Select all

.-------------------------.----------------------.----------------------.
|  49       579    4579   | 2      35679   3567  |  1      8      37    |
|  1289     3      1789   | 19     4       17    |  6      5      27    |
|  12       257    6      | 135    357     8     | b479   a2379   2347  |
:-------------------------+----------------------+----------------------:
|  5        689    189-3  | 7      368   d(4)6-3 |  2    a[3]9   c134   |
|  26       4      379    | 35     1       26    |  579    379    8     |
| f2(3)8-1  278    1378   | 458    2358    9     | b457    6    c[1]457 |
:-------------------------+----------------------+----------------------:
|  4689     1      459    | 489    25789   457   |  3      27     67    |
|  7        69   f(3)89-5 | 13589  2359    1235  |  58     4     c2[5]6 |
| e348      58     2      | 6      357    e3457  |  578    1      9     |
'-------------------------'----------------------'----------------------'

Step 9: (39)r43c8 = (94)r36c7 - @(514)r864c9 = (4)r4c6@ - (4,3)r9c61 = (3)r6c1&r8c3 => -3 r4c36, -1 r6c1, -5 r8c3

(Basics: 1 PP, 1 HP)

Step 10: -2 r7c5,r8c9: Show

Code: Select all

.-----------------.------------------------.---------------------.
| 49    579  45   | 2      35679    3567   |  1      8      37   |
| 1289  3    789  | 19     4        17     |  6      5      27   |
| 12    257  6    | 135    357      8      | b479   a2379   2347 |
:-----------------+------------------------+---------------------:
| 5     689  189  | 7      368     d46     |  2      39    c134  |
| 26    4    379  | 35     1       d26     |  579    379    8    |
| 238   278  1378 | 458    2358     9      | b457    6      1457 |
:-----------------+------------------------+---------------------:
| 4689  1    45   | 489    5789-2   457    |  3    a[2]7    67   |
| 7     69   389  | 13589  2359    d1(2)35 |  58     4      56-2 |
| 348   58   2    | 6      357      3457   |  578    1      9    |
'-----------------'------------------------'---------------------'

Step 10: (29)r73c8 = (94)r36c7 - r4c9 = (462)r458c6 => -2 r7c5,r8c9

(1 placement)

Step 11: -8 r8c3,r9c7: Show

Code: Select all

.--------------------.---------------------.------------------.
|  49     579   45   | 2      35679   3567 |  1     8    37   |
|  1289   3     789  | 19     4       17   |  6     5    27   |
|  12     257   6    | 135    357     8    |  479   379  2347 |
:--------------------+---------------------+------------------:
|  5     c689   189  | 7      368    d46   |  2     39   134  |
|  26     4     379  | 35     1       26   |  579   379  8    |
|  238    278   1378 | 458    2358    9    |  457   6    1457 |
:--------------------+---------------------+------------------:
|  4689   1    e45   | 489    5789    457  |  3     2    67   |
|  7     b69    39-8 | 13589  2359    1235 | a5[8]  4   a56   |
| e348   e5(8)  2    | 6      357    d3457 |  57-8  1    9    |
'--------------------'---------------------'------------------'

Step 11: (8=56)r8c79 - r8c2 = r4c2 - (64)r49c6 = (458)b7p738 => -8 r8c3,r9c7

(1 placement, 1 PP, 1 HP)

Step 12: -6 r7c1; btte: Show

Code: Select all

.-----------------------.-------------------------.------------------.
|   49       579   45   |  2         35679   3567 |  1    8     37   |
|   1289     3     789  |  19        4       17   |  6    5     27   |
|   12      a257   6    | C135      h357     8    |  479  379   2347 |
:-----------------------+-------------------------+------------------:
|   5        689   189  |  7         368     46   |  2    39    134  |
| bL2(6)     4     379  | D35        1      L26   | E579  379   8    |
|   238     b278   1378 |  48       K2358    9    |  457  6    F1457 |
:-----------------------+-------------------------+------------------:
|   49-6     1     45   |  48        5789    457  |  3    2   G(6)7  |
|   7     mN(6)9  m39   |  1359  iJmN2359    1235 |  8    4    G56   |
|   348      58    2    |  6         357     3457 |  57   1     9    |
'-----------------------'-------------------------'------------------'


Step 12: Double Kraken 5R3,8N5

Code: Select all

(5-2)r3c2 = (26)b4p84
||
(5)r3c4 - r5c4 = r5c7 - r6c9 = (56)r87c9
||
(5)r3c5 - (5)r8c5
          ||
          (2)r8c5 - r6c5 = (2,6)r5c61
          ||
          (396)r8c532
          ||
          (96)r8c52

=> -6 r7c1; btte (1 HP)

Now I really feel like I deserve my break I won't be solving sudokus for a while.

Edit: some stylistic changes to the chains and diagrams.

[Wecoc]

Hodoku v2.2.0 doesn't find anything using 1s there, but solves it using a Swordfish with 5s

Sorry, by that I meant it doesn't use the 1s to solve the puzzle directly (using Next Hint-Execute // Solve up to) in any moment, because prioritizes the Swordfish in 5s.
Of course if you use 'Find all steps' to search for that chain manually it does find pages of chains as you said, including the one I said.

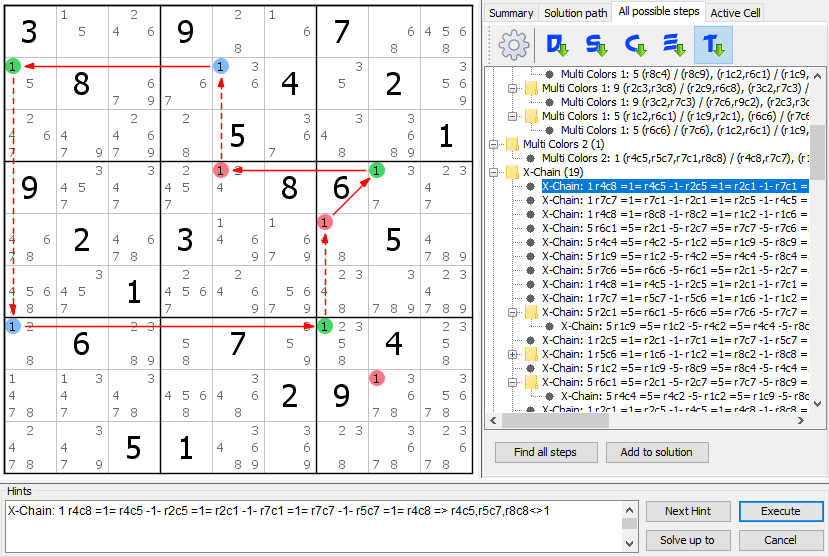
I think it's the first one on the list, indeed:
X-Chain: 1 r4c8 =1= r4c5 -1- r2c5 =1= r2c1 -1- r7c1 =1= r7c7 -1- r5c7 =1= r4c8 => r4c5,r5c7,r8c8<>1

Screen: Show

But the thing is, maybe here's where I'm wrong but comparing them I would say it was more time-consuming for the computer to find that chain than the Swordfish, yet the Slot Machine finds both basically in the same manner, and both crack the puzzle. That's where I was trying to focus on and it's why I pointed that example in the first place, it's all about processing speed.

- Could the Slot Machine method on the code be faster than the default method to find the Swordfish? (I don't think so)
- What about more complex chains also found by this technique, like Finned Swordfish, Multi-coloring, Nishio chains...? (Here's what I was aiming to test)

Because let's say this method is faster to find a specific type of chain, for example the Finned Swordfish; you could have it as a choice in the algorithm before the default, and reserve the default method for chains not found by the technique.

(A Finned Swordfish being slower than a Swordfish without fins, Sudoku truly is a crazy world )
That being said, maybe this is too much for me... for now I'll stop bothering with that before SpAce needs a long vacation because of my fault

[SpAce]

Hodoku v2.2.0 doesn't find anything using 1s there, but solves it using a Swordfish with 5s

Sorry, by that I meant it doesn't use the 1s to solve the puzzle directly (using Next Hint-Execute // Solve up to) in any moment, because prioritizes the Swordfish in 5s.
Of course if you use 'Find all steps' to search for that chain manually it does find pages of chains as you said, including the one I said.

Ok.

But the thing is, maybe here's where I'm wrong but comparing them I would say it was more time-consuming for the computer to find that chain than the Swordfish

Based on what? If you're still talking about Hodoku, how do you know it found one faster than the other? I don't see an easy way to draw that conclusion without adding some timers to the code. You obviously can't compare the speed of the "Next Hint" and "Find all steps" options because the former uses a pre-calculated step when the puzzle was initialized (and it only needs to find one for each step, based on the chosen hierarchy).

yet the Slot Machine finds both basically in the same manner, and both crack the puzzle. That's where I was trying to focus on and it's why I pointed that example in the first place, it's all about processing speed.

Well, I've only seen speed issues with Hodoku when the huge complex fish/fin options (mostly useless) are turned on, so I don't really see this as a high-priority optimization issue.

Because let's say this method is faster to find a specific type of chain, for example the Finned Swordfish; you could have it as a choice in the algorithm before the default, and reserve the default method for chains not found by the technique.

If you're coding a solver I'd recommend getting it to work first and then worry about speed. Premature optimization is bad because it leads to poorly maintainable code, and it might not give you any benefits at all. You should first implement all the functionality and then -- if you truly have performance issues -- find out exactly where the bottlenecks are and fix them. Early on your only performance-related worry should be on the architectural level, because it might be hard to change later on. Then again, I haven't coded a sudoku solver (except a very basic one), so this is just based on general software engineering wisdom.

(A Finned Swordfish being slower than a Swordfish without fins, Sudoku truly is a crazy world )

That being said, maybe this is too much for me... for now I'll stop bothering with that before SpAce needs a long vacation because of my fault

Don't worry about it. I'm taking a vacation from sudoku anyway. Dunno how long, though, as it seems to be difficult to even start it!

[SpAce]

Anyways what I wanted to test was if using this there was possible room for optimization on the algorithms or not (it was improbable but it was worth a shot), even if it really is just another fancy way to spot X-Chains.
As far as I tried, this sometimes finds Swordfish, Finned Swordfish, Nishio Forcing Chains or more exotic things, so it's not a trick focused on a very specific type of chain,

Well, that depends on what trick we're talking about. The actual trick it's using to find those various chains seems to be normal, ages old, coloring (a bit advanced variant). If that part is marketed as a totally new technique and renamed Slot Machine, it's at best ignorant and at worst outright dishonest.

Then again, the whole "Slot Machine" technique seems to be so poorly defined that I still don't know what it actually means. To me its only distinct feature is spotting a specific pattern of solved cells in the different chutes, which gives a high probability of finding single-digit chains -- or multi-digit chains if more than one such pattern is combined (Linked Slot Machine). The rest of the technique is just applying normal coloring on the pattern's candidates, possibly revealing those various chains or nets, which can be done with or without spotting the pattern (or knowing anything about the Slot Machine technique) -- and often gives results even when the pattern is not present.

The coloring part is definitely not specific to this technique, and there are actually more powerful coloring methods (like GEM) to get the same results and more. To me it seems that the only possibly new invention is the pattern of solved cells, and I kind of doubt that's very new either -- but I admit I hadn't seen it mentioned before.

but it also doesn't find them all nor is always applicable, so it would be complementary on the keith's technique, not a substitution.

As I've said from the beginning, I agree that it could work as a preliminary spotting aid, so I don't want to bash it too much. I was also very skeptical about keith's technique at first when Yogi talked about it, but ended up using it all the time especially in p&p solving. If the Slot Machine pattern is present, it could be an even quicker way to see existing single-digit potential, so it might be useful as a first step. However, if it's not present, it doesn't mean that single-digit chains aren't -- keith's technique will give you a more definite answer to that.

So you're right that it could be complementary to keith's technique, and should be applied first if both are used. One should still remember that both are just short-cuts, and neither is necessary. Coloring will give the same results (and more) regardless, but before it's started it's of course useful to know where the highest potential is. That's where the Slot Machine and keith's technique can help. The actual feature of the Slot Machine that finds those chains is coloring, but it's of course not a new invention.