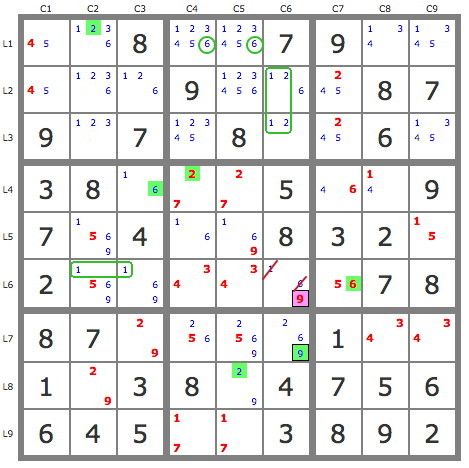
SpAce wrote:Woohoo, I installed and tried SudoRules for the first time:
Good.
You can also play with the configuration.
*** First puzzleUsing:
- Code: Select all
(bind ?*Subsets* TRUE)
the first puzzle has a path with only Subsets:
***********************************************************************************************
*** SudoRules 20.1.s based on CSP-Rules 2.1.s, config = S
*** Using CLIPS 6.32-r773
***********************************************************************************************
lots of singles
151 candidates, 773 csp-links and 773 links. Density = 6.83%
whip[1]: c1n5{r2 .} ==> r3c2 ≠ 5, r1c2 ≠ 5, r2c2 ≠ 5
hidden-pairs-in-a-row: r4{n2 n7}{c4 c5} ==> r4c5 ≠ 6, r4c5 ≠ 4, r4c5 ≠ 1, r4c4 ≠ 6, r4c4 ≠ 4, r4c4 ≠ 1
whip[1]: r4n4{c8 .} ==> r6c7 ≠ 4
hidden-pairs-in-a-row: r6{n3 n4}{c4 c5} ==> r6c5 ≠ 9, r6c5 ≠ 6, r6c5 ≠ 1, r6c4 ≠ 6, r6c4 ≠ 1
x-wing-in-columns: n9{c3 c6}{r6 r7} ==> r7c5 ≠ 9, r6c2 ≠ 9
swordfish-in-columns: n2{c3 c6 c7}{r2 r7 r3} ==> r7c5 ≠ 2, r7c4 ≠ 2, r3c4 ≠ 2, r3c2 ≠ 2, r2c5 ≠ 2, r2c2 ≠ 2
naked-pairs-in-a-block: b8{r7c4 r7c5}{n5 n6} ==> r7c6 ≠ 6
swordfish-in-columns: n6{c3 c6 c7}{r4 r2 r6} ==> r6c2 ≠ 6, r2c5 ≠ 6, r2c2 ≠ 6
naked-pairs-in-a-block: b1{r2c2 r3c2}{n1 n3} ==> r2c3 ≠ 1, r1c2 ≠ 3, r1c2 ≠ 1
whip[1]: c3n1{r6 .} ==> r5c2 ≠ 1, r6c2 ≠ 1
stte
Subsets are not enough for the second puzzle. Adding only bivalue-chains is still not enough. Adding z-chains is enough, but at the cost of having long ones (length 8):
- Code: Select all
(bind ?*Subsets* TRUE)
(bind ?*Bivalue-Chains* TRUE)
(bind ?*z-Chains* TRUE)
***********************************************************************************************
*** SudoRules 20.1.s based on CSP-Rules 2.1.s, config = Z+S
*** Using CLIPS 6.32-r773
***********************************************************************************************
naked-single ==> r9c8 = 4, r5c1 = 2, r9c7 = 7, r9c4 = 8, r4c9 = 8, r1c2 = 8
184 candidates, 1145 csp-links and 1145 links. Density = 6.8%
whip[1]: c7n6{r5 .} ==> r6c9 ≠ 6
whip[1]: c7n5{r3 .} ==> r3c9 ≠ 5, r1c9 ≠ 5
whip[1]: c1n4{r2 .} ==> r3c3 ≠ 4, r1c3 ≠ 4, r2c3 ≠ 4
whip[1]: c1n3{r2 .} ==> r3c3 ≠ 3, r1c3 ≠ 3, r2c3 ≠ 3
hidden-pairs-in-a-row: r5{n5 n7}{c4 c5} ==> r5c5 ≠ 6, r5c5 ≠ 3, r5c5 ≠ 1, r5c4 ≠ 6, r5c4 ≠ 3, r5c4 ≠ 1
whip[1]: r5n3{c8 .} ==> r4c7 ≠ 3
hidden-pairs-in-a-row: r4{n2 n3}{c4 c5} ==> r4c5 ≠ 9, r4c5 ≠ 6, r4c5 ≠ 1, r4c4 ≠ 6, r4c4 ≠ 1
x-wing-in-rows: n9{r6 r9}{c3 c5} ==> r7c5 ≠ 9, r7c3 ≠ 9, r4c3 ≠ 9
z-chain[2]: c2n7{r3 r7} - c6n7{r7 .} ==> r3c4 ≠ 7
biv-chain[3]: r5c2{n1 n6} - b6n6{r5c7 r4c7} - r4n4{c7 c3} ==> r4c3 ≠ 1
naked-pairs-in-a-row: r4{c3 c7}{n4 n6} ==> r4c6 ≠ 6, r4c2 ≠ 6
whip[1]: b5n6{r6c5 .} ==> r6c3 ≠ 6
z-chain[3]: c7n5{r2 r3} - c2n5{r3 r7} - c6n5{r7 .} ==> r2c5 ≠ 5
z-chain[3]: c7n5{r3 r2} - c2n5{r2 r7} - c6n5{r7 .} ==> r3c4 ≠ 5
z-chain[6]: r9c3{n5 n9} - r6n9{c3 c5} - r4c6{n9 n1} - r3c6{n1 n7} - c2n7{r3 r7} - c2n5{r7 .} ==> r3c3 ≠ 5
;;; Resolution state RS1
z-chain[8]: r5c2{n1 n6} - r2c2{n6 n5} - c7n5{r2 r3} - r3c6{n5 n7} - r3c3{n7 n2} - r2n2{c3 c5} - r2n1{c5 c6} - r4n1{c6 .} ==> r3c2 ≠ 1
z-chain[5]: r3c2{n7 n5} - r3c6{n5 n1} - r4c6{n1 n9} - c2n9{r4 r7} - c2n7{r7 .} ==> r3c3 ≠ 7
z-chain[7]: r1n5{c6 c3} - r9c3{n5 n9} - r7n9{c2 c6} - r4c6{n9 n1} - r3c6{n1 n7} - r3c2{n7 n5} - c7n5{r3 .} ==> r2c6 ≠ 5
biv-chain[3]: r4n1{c2 c6} - r2c6{n1 n6} - c2n6{r2 r5} ==> r5c2 ≠ 1
singles ==> r5c2 = 6, r4c3 = 4, r4c7 = 6, r5c7 = 3, r5c8 = 1, r6c9 = 4
z-chain[2]: c2n1{r2 r4} - c6n1{r4 .} ==> r2c5 ≠ 1
biv-chain[3]: r4c4{n2 n3} - r3n3{c4 c9} - r1c8{n3 n2} ==> r1c4 ≠ 2
biv-chain[3]: r2c2{n5 n1} - r2c6{n1 n6} - c3n6{r2 r1} ==> r1c3 ≠ 5
whip[1]: r1n5{c6 .} ==> r3c6 ≠ 5
biv-chain[3]: c9n1{r1 r3} - r3c6{n1 n7} - b1n7{r3c2 r1c3} ==> r1c3 ≠ 1
biv-chain[3]: r3c3{n2 n1} - r3c6{n1 n7} - b1n7{r3c2 r1c3} ==> r1c3 ≠ 2
biv-chain[3]: r3c6{n1 n7} - r3c2{n7 n5} - r2c2{n5 n1} ==> r2c6 ≠ 1, r3c3 ≠ 1
stte
What about adding t-whips to the above?
- Code: Select all
(bind ?*Subsets* TRUE)
(bind ?*Bivalue-Chains* TRUE)
(bind ?*z-Chains* TRUE)
(bind ?*t-Whips* TRUE)
We now get a solution with chains length ≤ 6:
***********************************************************************************************
*** SudoRules 20.1.s based on CSP-Rules 2.1.s, config = tW+S
*** Using CLIPS 6.32-r773
***********************************************************************************************
;;; Same path as before to resolution state RS1
t-whip[6]: r4n1{c6 c2} - r5c2{n1 n6} - r2c2{n6 n5} - c7n5{r2 r3} - r3c2{n5 n7} - r3c6{n7 .} ==> r2c6 ≠ 1, r1c6 ≠ 1
t-whip[3]: b3n1{r1c9 r3c9} - c6n1{r3 r4} - r6n1{c4 .} ==> r1c3 ≠ 1
biv-chain[4]: r5c7{n3 n6} - c2n6{r5 r2} - r2c6{n6 n5} - b3n5{r2c7 r3c7} ==> r3c7 ≠ 3
z-chain[3]: r4c4{n2 n3} - r3n3{c4 c9} - b3n2{r3c9 .} ==> r1c4 ≠ 2
z-chain[4]: r3c7{n4 n5} - r2c7{n5 n3} - r3n3{c9 c4} - r3n4{c4 .} ==> r1c9 ≠ 4
t-whip[4]: r2c6{n6 n5} - r1n5{c6 c3} - c2n5{r3 r7} - r7n9{c2 .} ==> r7c6 ≠ 6
whip[1]: c6n6{r2 .} ==> r1c4 ≠ 6, r1c5 ≠ 6, r2c5 ≠ 6
z-chain[3]: r1n5{c6 c3} - r1n6{c3 c6} - r2c6{n6 .} ==> r3c6 ≠ 5
t-whip[3]: r1n6{c3 c6} - r2c6{n6 n5} - r1n5{c4 .} ==> r1c3 ≠ 7, r1c3 ≠ 2
whip[1]: r1n7{c6 .} ==> r3c6 ≠ 7
stte
What if we add the full power of whips or g-whips? Nothing new. Some of them appear in the resolution path, but the max length of chains remains 6.
Now that we have found the combination of chains that give the best result, we can try to restrict it to the corresponding 2D-chains:
- Code: Select all
(bind ?*Subsets* TRUE)
(bind ?*Typed-Bivalue-Chains* TRUE)
(bind ?*Typed-z-Chains* TRUE)
(bind ?*Typed-t-Whips* TRUE)
We still get a solution, but the necessary chains are much longer (length 24). As this is not interesting, I skip it.
We can also try to introduce typed-whips, but then we need chains of length 8. This is not too much above the optimal 6, so it may be interesting for players who like 2D-chains.
Notice that I don't apply the above progressive method when I have to solve long lists of puzzles.
The fastest approach is to activate only whips in order to get a first estimate of the difficulty.
An alternative approach is to use the default configuration, where all the special cases of whips are activated. This gives an idea of what chains might not be necessary. But this may be too computationally heavy for extremely hard puzzles.
As you can see, there are many possibilities and one is free to choose what he considers the one he likes best.