The New Sudoku Players' Forum

[SteveG48]

Code: Select all

 *-----------*
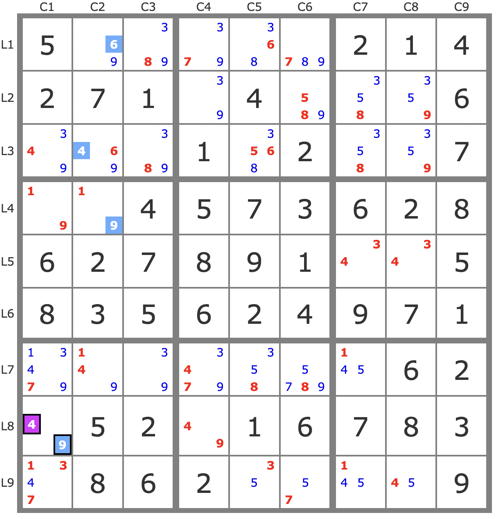
 |5..|...|21.|
 |271|.4.|...|
 |...|...|...|
 |---+---+---|
 |..4|57.|628|
 |...|8.1|...|
 |835|.24|9..|
 |---+---+---|
 |...|...|...|
 |...|.1.|783|
 |.86|...|..9|
 *-----------*


[P.O.]

Code: Select all

after singles:
5      69     389    379    368    789    2      1      4               
2      7      1      39     4      589    358    359    6               
349    469    389    1      3568   2      358    359    7               
19     19     4      5      7      3      6      2      8               
6      2      7      8      9      1      34     34     5               
8      3      5      6      2      4      9      7      1               
13479  149    39     3479   358    5789   145    6      2               
49     5      2      49     1      6      7      8      3               
1347   8      6      2      35     57     145    45     9         

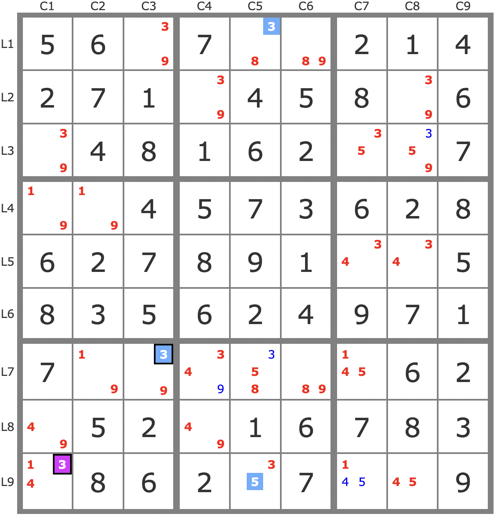
9r2c4 => r1c5 <> 3,6,8
 r2c4=9 - r8n9{c4 c1} - r7c3{n9 n3} - r9n3{c1 c5}
 r2c4=9 - r8n9{c4 c1} - r4n9{c1 c2} - r1c2{n9 n6}
 r2c4=9 - c6n9{r12 r7} - r7n8{c6 c5}
 
=> r2c4 <> 9
ste.


or the same elimination with a rather longish linear contradiction chain:

Code: Select all

9r2c4 => r4c12 <> 9
 r2c4=9 - r8n9{c4 c1} - r7c3{n9 n3} - 47r78c4 - r9c6{n7 n5} - r2c6{n59 n8} - 36r1c45 - r1c2{n6 n9}
 
=> r2c4 <> 9
ste.


[Mauriès Robert]

Hi,
Here's a resolution in two short steps.
1) (-4r8c1) => 9r8c1->(9r4c2->6r1c2)->4r3c2->... => -4r3c1 + basics.

Hidden Text: Show

2) (-3r9c1) => 3r7c3->3r1c5->5r9c5->... => -3r9c5, end.

Hidden Text: Show

[Cenoman]

As already shown by yzfwsf in past puzzles, the "Fireworks" pattern (inventor: shye - congratulations !) enables simplified chains. I had decided to learn how to spot one. The present puzzle is an opportunity.

Code: Select all

 +----------------------+-----------------------+-------------------+
 |  5      g69   b38-9* | c379*  f368   c789    |  2     1     4    |
 |  2       7     1     |  39     4     e589    |  358   359   6    |
 |  349     469   38-9  |  1     f3568   2      |  358   359   7    |
 +----------------------+-----------------------+-------------------+
 |  19      19    4     |  5      7      3      |  6     2     8    |
 |  6       2     7     |  8      9      1      |  34    34    5    |
 |  8       3     5     |  6      2      4      |  9     7     1    |
 +----------------------+-----------------------+-------------------+
 |  13479   149  a39    | b3479*  358    5789   |  145   6     2    |
 |  49      5     2     |  49     1      6      |  7     8     3    |
 |  1347    8     6     |  2      35    d57     |  145   45    9    |
 +----------------------+-----------------------+-------------------+

Fireworks (3)r1, c4, b2 (only one candidate 3 out of b2 in r1, and c4) => at least one out of 3r1c3, 3r1c4, 3r7c4 is True
Hence the AIC:
(9=3)r7c3 - (3)r1c3|r7c4 =FW= (37)r1c46 - (7=5)r9c6 - r2c6 = (56)r13c5 - (6=9)r1c2 => -9 r13c3; ste
Edit: corrected typo. Thanks JCO

[Cenoman]

Here's a resolution in two short steps.

Glad to see you back, Robert !

[jco]

Fireworks (3)r1, c4, b2 (only one candidate 3 out of b2 in r1, and c4) => at least one out of 3r1c3, 3r1c4, 3r7c4 is True
Hence the AIC:
(9=3)r7c3 - (3)r1c3|r7c4 =FW= (37)r1c46 - (7=5)r9c6 - r2c6 = (56)r13c5 = (6=9)r1c2 => -9 r13c3; ste

Nice!
This reminds me of an unanswered question (that I saw today morning).