The New Sudoku Players' Forum

[gurth]

Another new SER 7.1 puzzle:

Code: Select all

 *-----------*
 |.2.|..3|.1.|
 |5..|.4.|7..|
 |...|...|..3|
 |---+---+---|
 |.3.|8.1|...|
 |..5|.6.|...|
 |71.|..9|...|
 |---+---+---|
 |...|...|.9.|
 |..2|6..|8..|
 |.9.|..4|..1|
 *-----------*


[Leren]

Messy Network 1 Stepper - I think I'll pass on marking the PM up.

Code: Select all

*--------------------------------------------------------------------------------*
| 468     2       9        | 57      8-7     3        | 456     1       4568     |
| 5       68      3        | 1       4       26       | 7       268     9        |
| 468     7       1        | 9       28      256      | 2456    24568   3        |
|--------------------------+--------------------------+--------------------------|
| 2       3       46       | 8       57      1        | 9       4567    4567     |
| 9       48      5        | 3       6       27       | 1       2478    2478     |
| 7       1       68       | 4       25      9        | 3       2568    2568     |
|--------------------------+--------------------------+--------------------------|
| 3       456     47       | 257     1       8        | 2456    9       24567    |
| 1       45      2        | 6       9       57       | 8       3       457      |
| 68      9       78       | 257     3       4        | 256     2567    1        |
*--------------------------------------------------------------------------------*

Kraken Column 8 Digit 6 :

6 r3c8 - r3c6 = r2c6 - r2c2 = (6-5) r7c2 = r8c2 - r8c6 = r3c6 - (5=7) r1c4 - 7 r1c5;

6 r4c8 - 7 r4c8 = r4c9 - r8c9 = r8c6 - r5c6 = r4c5                         - 7 r1c5;
               || r4c5                                                     - 7 r1c5;

6 r6c8 - r6c3 = (6-4) r4c3 = r5c2 - r8c2 = (4-7) r8c9 = r8c6 - r5c6 = r4c5 - 7 r1c5;

6 r9c8 - r9c1 = (6-5) r7c2 = r8c2 - r8c6 = r3c6 - (5=7) r1c4  - 7 r1c5; => - 7 r1c5; stte

Leren

[eleven]

Code: Select all

    *--------------------------------------------------------------------------------*
    |c468*    2       9        | 57     @78      3        |#456     1     @#4568     |
    | 5      b68      3        | 1       4       26       | 7      a268     9        |
    |c468     7       1        | 9       28      256      | 2456    24568   3        |
    |--------------------------+--------------------------+--------------------------|
    | 2       3       46       | 8       57      1        | 9       4567    4567     |
    | 9       48      5        | 3       6       27       | 1       2478    2478     |
    | 7       1       68       | 4       25      9        | 3       2568    2568     |
    |--------------------------+--------------------------+--------------------------|
    | 3      e456*    47*      | 257     1       8        |#2456    9      #24567    |
    | 1       45      2        | 6       9       57       | 8       3       457      |
    |d68      9       78       | 257     3       4        | 256     2567    1        |
    *--------------------------------------------------------------------------------*

UR 46r17c68: SIS(-5r7c2,4r7c3,-8r1c1=8r1c59)
-5r8c2=5r8c2
4r7c3-(4=5)r8c2
(8-7)r1c5=(7-5)r1c4=5r3c6
8r1c9-r2c8=r2c2-r13c1=(8-6)r9c1=(6-5)r7c2=5r8c2
=> -5r8c6

[JC Van Hay]

After basics, including XWings on 2, 4, 7 and 8 => NP(56)B6, ...

Code: Select all

+----------------+-------------------+----------------------+
| 468  2      9  | (57)  8-7   3     | 456   1      468(5)  |
| 5    68     3  | 1     4     26    | 7     268    9       |
| 468  7      1  | 9     28    26(5) | 2456  24568  3       |
+----------------+-------------------+----------------------+
| 2    3      46 | 8     (57)  1     | 9     47     6(5)    |
| 9    48     5  | 3     6     27    | 1     2478   2478    |
| 7    1      68 | 4     25    9     | 3     56     28      |
+----------------+-------------------+----------------------+
| 3    46(5)  47 | 257   1     8     | 2456  9      2467(5) |
| 1    4(5)   2  | 6     9     7(5)  | 8     3      47(5)   |
| 68   9      78 | 257   3     4     | 256   2567   1       |
+----------------+-------------------+----------------------+


WWing : (7=5)r4c5 - 5r4c9=*[5r1c9=*XWing(5r78c29) - 5r8c6=5r3c6] - (5=7)r1c4 :=> -7r1c5; stte

OR

Code: Select all

+-------------------+----------------+----------------------+
| 48(6)  2     9    | 57   78  3     | 456   1        4568  |
| 5      (68)  3    | 1    4   2(6)  | 7     28(6)    9     |
| 48(6)  7     1    | 9    28  25(6) | 2456  2458(6)  3     |
+-------------------+----------------+----------------------+
| 2      3     46   | 8    57  1     | 9     47       56    |
| 9      4-8   5    | 3    6   27    | 1     2478     2478  |
| 7      1     (68) | 4    25  9     | 3     5(6)     28    |
+-------------------+----------------+----------------------+
| 3      456   47   | 257  1   8     | 2456  9        24567 |
| 1      45    2    | 6    9   57    | 8     3        457   |
| 8(6)   9     78   | 257  3   4     | 256   257(6)   1     |
+-------------------+----------------+----------------------+


WWing : (8=6)r6c3 - 6r6c8=*[6r13c1=6r9c1 - 6r9c8=*XWing(6r23c68)] -(6=8)r2c2 :=> -8r5c2; stte

[gurth]

CW: see diagram: start at "a", r8c2.

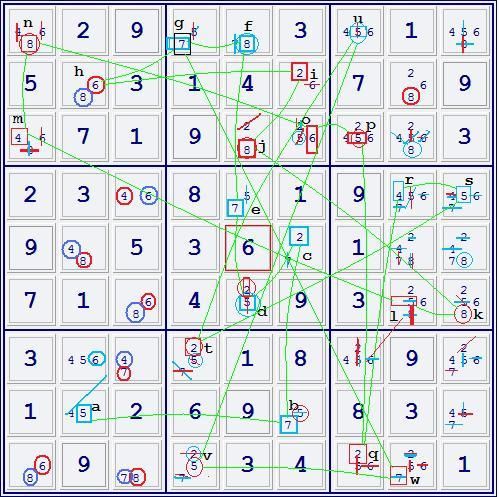
Comments:
While this solution is still long, involving 23 cells, it is less than half the length that 534se71 took. That is because there were far more bivalues on offer. That led to more interactions between red and blue, which eventually agreed in cutting 514. No contradictions anywhere. I found 714 solved the puzzle by singles only, without even knowing which colour was true.

Now that I've done my fair share of struggling with this one, I'll let the cat out of the bag: this puzzle is actually a scrambled version of a ST (Symmetry Technique) puzzle. Any readers interested in ST might like to unscramble and solve - I haven't yet tried myself, and it wouldn't really be fair for me to post a solution as I was the one who did the scrambling, even though the scrambling in this case will be very easy to unravel.

[JC Van Hay]

I found 714 solved the puzzle by singles only, without even knowing which colour was true.

No wonder as I mentioned in an earlier comment : if a=A, a -> contradiction, A -> solution, then the exclusions due to the colors transport from (aA) [CW, GEM, RGT, ...] suffices to solve the puzzle without knowing which color is True/False. Here, 482 -> contradiction and 582 -> solution.

Now that I've done my fair share of struggling with this one, I'll let the cat out of the bag: this puzzle is actually a scrambled version of a ST (Symmetry Technique) puzzle. Any readers interested in ST might like to unscramble and solve - I haven't yet tried myself, and it wouldn't really be fair for me to post a solution as I was the one who did the scrambling, even though the scrambling in this case will be very easy to unravel.

The symmetries of the puzzle were obvious from the very start while filling the unsolved cells with candidates digit after digit : the clusters for the 2s and 4s were similar as well as for the 5s and 6s, the 7s and the 8s. I even suspected that you were responsible for the clumsy "scrambling" : 2<->4, 5<->6, 7<->8; Band1<->Band3, Stack1<->Stack2, C2<->C3, C5<->C6, R1<->R3, R4<->R6, C8<->C9, ... Finally, I took more or less into account these symmetries in the solutions I posted above !

[daj95376]

Couldn't follow eleven's logic, so I condensed a solution found by my solver.

Code: Select all

 +-----------------------------------------------------------------------+
 |  468    2      9      | a57     78     3      |  456    1      4568   |
 |  5     f68     3      |  1      4      26     |  7     g268    9      |
 |  468    7      1      |  9      28    b256    |  2456   24568  3      |
 |-----------------------+-----------------------+-----------------------|
 |  2      3      46     |  8      57     1      |  9      4567   4567   |
 |  9     e48     5      |  3      6      27     |  1      2478   2478   |
 |  7      1      68     |  4      25     9      |  3      2568   2568   |
 |-----------------------+-----------------------+-----------------------|
 |  3     E456   F47     | G257    1      8      |  2456   9      24567  |
 |  1     d45     2      |  6      9     c57     |  8      3      457    |
 |  68     9      78     |  257    3      4      |  256    2567   1      |
 +-----------------------------------------------------------------------+
 # 74 eliminations remain

 =5r1c4 =5r8c6 =5r7c2                \    -> -5  r17c79
               =4r8c2 =7r7c3 =2r7c4   \   -> -72 r 7c79
                      =8r5c2 =8r2c8    \  -> -8  r1 c79

                                          ->    [r17c79]=DP46  =>  -5 r1c4


_

[eleven]

Couldn't follow eleven's logic, so I condensed a solution found by my solver.

Danny, my logic is:
4 or 6 must be outside the DP either in row 1 or in row 7, otherwise they are (hidden) pairs in a deadly pattern.
In row 1: if 4 or 6 are in r1c1, 8 cannot be there and must be in r1c5 (implies 5r3c6) or r1c8 (implies 5r8c2).
In row 7: if 4 or 6 are in r7c2, then 5 is in r8c2. If 4 is in r7c3 also r8c2=5.

... this puzzle is actually a scrambled version of a ST (Symmetry Technique) puzzle.

Interesting, i did not notice, because i only looked at 2 DP's, then i saw that the second solved it.

Puzzles with digit symmetry are so rare, that checking it is a waste of time, but as JC mentioned, you might find it out, if you notice, that you always can make the same move for 2 digits.

The symmetric digits are 2/4, 7/8, 5/6, 3/9, 1 is single.
The "center" box is b6, symmetric are boxes 1/8, 2/7, 4/5 and 3/9.
From the positions of digits 139 you can find the symmetric cells easily in their mini-lines.
E.g. if you look for the symmetric cell of r1c1 with 29 in the minirow, you find 43 in box 8, so it must be r9c4.

However i could not find something good to crack the puzzle using symmetry.
Did you see a solution for the unscrambled puzzle ?

Moves like this one
5r8c6=5r3c6/6r7c2-(6=5)r8c2
don't help much and can be found without symmetry too (with one more link).

[gurth]

Puzzles with digit symmetry are so rare, that checking it is a waste of time, but as JC mentioned, you might find it out, if you notice, that you always can make the same move for 2 digits.

However i could not find something good to crack the puzzle using symmetry.
Did you see a solution for the unscrambled puzzle ?

Moves like this one
5r8c6=5r3c6/6r7c2-(6=5)r8c2
don't help much and can be found without symmetry too (with one more link).

However, if it is known or suspected that I composed the puzzle, then the records (see the thread Gurth's Puzzles) will show that a considerable percentage of my compositions are symmetry puzzles!
I haven't tried to solve it by symmetry. I've forgotten the symmetry techniques and now prefer to study something else.

[eleven]

Ok, if i had not missed something, this is the puzzle, where digital symmetry offered the least help for solving.