The New Sudoku Players' Forum

[Gee]

Number I have read somewhere about having three strong links that can be used to solve an X-Wing. With that, I have saved various puzzles where I have come across X-Wings that fit this description. I cannot find anything written about this but I think I have seen a posting on this forum relating to using three strong as a method of solving for a candidate. I may be all wrong, but please look at each of the below and let me know if I “barking up the wrong tree”.


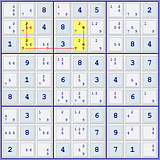
The puzzles have the rectangle’s candidates are
labeled as (a)b (b),(c) and (d).

Number 1: On (4’s)
(4) Locked on bd
(4) Locked on cd
(7) Locked on cd
(d) can be made a (4)
(a) can be made a (4)

Code: Select all

 
 *--------------------------------------------------*
 | 6    249  7    | 1    8    5    | 24a   3    49b  |
 | 3    459  459  | 69   2    7    | 46   8    1    |
 | 29   1    8    | 69   4    3    | 256  7    59   |
 |----------------+----------------+----------------|
 | 489  789  49   | 47   5    6    | 3    1    2    |
 | 24   27   1    | 47   3    9    | 8    5    6    |
 | 5    3    6    | 2    1    8    | 47c   9    47d  |
 |----------------+----------------+----------------|
 | 7    489  349  | 5    69   2    | 1    46   38   |
 | 1    6    359  | 8    79   4    | 57   2    357  |
 | 48   458  2    | 3    67   1    | 9    46   578  |
 *--------------------------------------------------*


Number (2) On (7’s)
(4) Locked ab
(7) Locked on ab
(7) Locked on ac
(a) can be made a (7)
(d) can be made a (7)

Code: Select all

 *-----------*
 
 *--------------------------------------------------*
 | 6    249  7    | 1    8    5    | 24   3    49   |
 | 3    459  459  | 69   2    7    | 46   8    1    |
 | 29   1    8    | 69   4    3    | 256  7    59   |
 |----------------+----------------+----------------|
 | 489  789  49   | 47   5    6    | 3    1    2    |
 | 24   27   1    | 47   3    9    | 8    5    6    |
 | 5    3    6    | 2    1    8    | 47a  9    47b  |
 |----------------+----------------+----------------|
 | 7    489  349  | 5    69   2    | 1    46   38   |
 | 1    6    359  | 8    79   4    | 57c  2    357d |
 | 48   458  2    | 3    67   1    | 9    46   578  |
 *--------------------------------------------------*


Number(3) on (5’s)
(5) Locked on bd
(5) Locked on cd
(6) Locked on ab

Code: Select all

 
 *-----------------------------------------------------------*
 | 2349  49    234   | 7     46    1     | 8     5     36    |
 | 1     6     5     | 3     8     9     | 4     7     2     |
 | 7     8     34    | 56    45    2     | 36    1     9     |
 |-------------------+-------------------+-------------------|
 | 456a 45    8     | 1     7     3     | 2     9     456b  |
 | 69    1479  1467  | 8     2     5     | 136   346   1346  |
 | 25c   3     12    | 4     9     6     | 7     8     15d   |
 |-------------------+-------------------+-------------------|
 | 8     2     136   | 56    135   4     | 9     36    7     |
 | 346   14    9     | 2     136   7     | 5     346   8     |
 | 3456  457   3467  | 9     36    8     | 136   2     1346  |
 *-----------------------------------------------------------*



Number (4) on (4’s)
This is different. It has four locked candidates and I can figure out
That (d) equals 4. This I took this from a Forum sometime back but have no idea
which post it came from.

6 Locked on ab
7 Locked on ac
4 Locked on cd
4 locked on bd

Code: Select all

 
 *--------------------------------------------------------------------*
 | 12     126    5      | 16     3      7      | 4      8      9      |
 | 149    14679a 149    | 1469b  2      8      | 5      137    37     |
 | 8      1479c  3      | 149d   19     5      | 2      17     6      |
 |----------------------+----------------------+----------------------|
 | 1349   8      7      | 2      5      149    | 6      349    34     |
 | 5      1349   149    | 189    19     6      | 7      349    2      |
 | 6      49     2      | 3      7      49     | 8      5      1      |
 |----------------------+----------------------+----------------------|
 | 7      159    6      | 159    4      3      | 19     2      8      |
 | 1249   12459  149    | 1579   8      19     | 3      6      47     |
 | 1349   1349   8      | 179    6      2      | 19     1479   5      |
 *--------------------------------------------------------------------*



Is there any way to solve x-wings as in the first three examples? I could not find a common denominator for doing so. I must have misunderstood what I read about three strong links and would appreciate your comments and corrections about the use of three strong links.

Thanks.

[Luke]

Code: Select all

 *--------------------------------------------------------------------*
 | 12     126    5      | 16     3      7      | 4      8      9      |
 | 149    14679a 149    | 1469b  2      8      | 5      137    37     |
 | 8      1479c  3      | 149d   19     5      | 2      17     6      |
 |----------------------+----------------------+----------------------|
 | 1349   8      7      | 2      5      149    | 6      349    34     |
 | 5      1349   149    | 189    19     6      | 7      349    2      |
 | 6      49     2      | 3      7      49     | 8      5      1      |
 |----------------------+----------------------+----------------------|
 | 7      159    6      | 159    4      3      | 19     2      8      |
 | 1249   12459  149    | 1579   8      19     | 3      6      47     |
 | 1349   1349   8      | 179    6      2      | 19     1479   5      |
 *--------------------------------------------------------------------*

This is udosuk's "strong wing" from here.

The first three do not fit the pattern I believe you are looking for. Check here. I think you need three strong links on different candidates, and conjugate pairs like your [47] are not involved.

Added:

If I understand this correctly, even having three strong links is not enough. There must be a weak link as well. The strong links form three sides of the rectangle, and the weak link completes it.

For example, this looked promising from your third PM:

Code: Select all

*-----------------------------------------------------------*
 | 2349  49    234   | 7     46    1     | 8     5     36    |
 | 1     6     5     | 3     8     9     | 4     7     2     |
 | 7     8    *34    | 56   *45    2     | 36    1     9     |
 |-------------------+-------------------+-------------------|
 | 456   45    8     | 1     7     3     | 2     9     456   |
 | 69    1479  1467  | 8     2     5     | 136   346   1346  |
 | 25    3     12    | 4     9     6     | 7     8     15    |
 |-------------------+-------------------+-------------------|
 | 8     2    *136   | 56   *135   4     | 9     36    7     |
 | 346   14    9     | 2     136   7     | 5     346   8     |
 | 3456  457   3467  | 9     36    8     | 136   2     1346  |
 *-----------------------------------------------------------*

I noticed that all the rectangles you cited were in two boxes, UR style. That's fine , but these rectangles don't have that same restriction. Here's one in four boxes. The cells designated above have three strong links on [145] but there is no weak link on 1 or 4 to seal the deal @ r37c3. Too bad! No elimination.

[Luke]

Here’s one with the necessary weak link. Strong links on [267] and weak on both 2 and 6.

Code: Select all

Ruud’s Nightmare 11-10-07
 *-----------------------------------------------------------*
 | 369   67    8     | 179   4     5     | 136   79    2     |
 | 359  *2567  4     | 8    *267   129   | 356   579   19    |
 | 1    *2567  569   | 3    *2679  29    | 56    8     4     |
 |-------------------+-------------------+-------------------|
 | 56    9     256   | 125   8     4     | 125   3     7     |
 | 57    1     257   | 6     259   3     | 4     59    8     |
 | 8     4     3     | 2579  2579  129   | 25    6     19    |
 |-------------------+-------------------+-------------------|
 | 479   3     179   | 29    129   6     | 8     24    5     |
 | 456   8     156   | 25    1235  7     | 9     24    36    |
 | 2     56    69    | 4     359   8     | 7     1     36    |
 *-----------------------------------------------------------*

I use these because I find them easy to spot. Others will see them as forcing chains or discontinuous nice loops.

[udosuk]

Here’s one with the necessary weak link. Strong links on [267] and weak on both 2 and 6.

Code: Select all

Ruud’s Nightmare 11-10-07
 *-----------------------------------------------------------*
 | 369   67    8     | 179   4     5     | 136   79    2     |
 | 359  *2567  4     | 8    *267   129   | 356   579   19    |
 | 1    *2567  569   | 3    *2679  29    | 56    8     4     |
 |-------------------+-------------------+-------------------|
 | 56    9     256   | 125   8     4     | 125   3     7     |
 | 57    1     257   | 6     259   3     | 4     59    8     |
 | 8     4     3     | 2579  2579  129   | 25    6     19    |
 |-------------------+-------------------+-------------------|
 | 479   3     179   | 29    129   6     | 8     24    5     |
 | 456   8     156   | 25    1235  7     | 9     24    36    |
 | 2     56    69    | 4     359   8     | 7     1     36    |
 *-----------------------------------------------------------*

A straight forward way to see this is:
r3c25 must contain a 7
=> r3c25 can't be [26]
=> either r2c2=2 or r2c5=6 (or both)

Hence r2c2<>6 & r2c5<>2.

Another side effect is r2c25 must have 2 or 6 (or both). So if there is a cell elsewhere on r2 with candidates {26} only, then it will form a "killer naked pair" of {26} with r2c25 on r2.