The New Sudoku Players' Forum

[Yogi]

....2..7..8....5...1..........1.8...7......2....5.....2..46...33.....4........1..

Code: Select all

+---+---+---+
|...|.2.|.7.|
|.8.|...|5..|
|.1.|...|...|
+---+---+---+
|...|1.8|...|
|7..|...|.2.|
|...|5..|...|
+---+---+---+
|2..|46.|..3|
|3..|...|4..|
|...|...|1..|
+---+---+---+


[Mauriès Robert]

Hi all,
My resolution with TDP after simplifying the puzzle with basic techniques.

(-7r7c7)->89r57c7->8r1c9->4r3c9->4r4c1->4r6c8->8r7c8->... => -8r7c7 => r7c8=8 => 12 placements

puzzle1: Show

(-7r7c7)->9r7c7->[ 6r1c7 and 6r9c8 ]->6r6c9->3r6c2->4r1c2->7r9c2->... => -7r9c9, stte

puzzle2: Show

Robert

[shye]

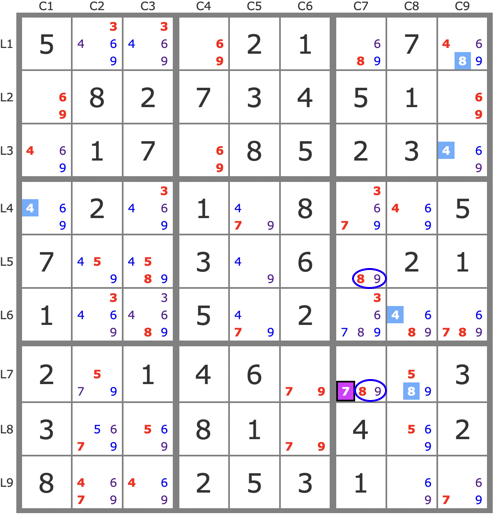
1) CNL
5r5c2 = (5-8)r5c3 = 8r5c7 - 8r7c7 = (8-5)r7c8 = 5r7c2 - 5r5c2 loop
=> -49r5c3, -8r16c7, -9r7c8, -5r8c2
many singles, and some lc's: 6c1>b1, 9c1>b1, 6r8>b7

2) m-wing
(6=9)r9c8 - 9r9c3 = (9-6)r8c3 = 6r4c3
=> -6r4c8
some singles

3) BUG+1
=> +6r6c7

[P.O.]

Code: Select all

( n1r6c1   n2r3c7   n2r6c6   n8r9c1   n1r2c8   n1r5c9   n2r4c2
  n2r2c3   n7r3c3   n1r8c5   n1r1c6   n8r8c4   n8r3c5   n1r7c3
  n2r8c9   n2r9c4   n5r9c5   n5r3c6   n7r2c4   n3r9c6   n5r4c9
  n3r2c5   n4r2c6   n5r1c1   n6r5c6   n3r5c4   n3r3c8 )

intersection:
((((4 0) (4 8 6) (4 6 9)) ((4 0) (6 8 6) (4 6 8 9))))

c8n4{r6 r4} - c1n4{r4 r3} - c9n4{r3 r1} - c9n8{r1 r6} => r6c8 <> 8

( n8r7c8   n5r8c8   n5r7c2   n5r5c3   n8r5c7   n8r6c3   n8r1c9
  n4r3c9   n4r4c1   n9r5c2   n4r5c5   n4r6c8 )

intersections:
((((9 0) (8 3 7) (6 9)) ((9 0) (9 3 7) (4 6 9)))
 (((6 0) (9 8 9) (6 9)) ((6 0) (9 9 9) (6 7 9)))
 (((6 0) (2 1 1) (6 9)) ((6 0) (3 1 1) (6 9))))
 
r8c2{n6 n7} - r9n7{c2 c9} - r7c7{n7 n9} - r1c7{n9 n6} - c9n6{r2 r6} => r6c2 <> 6
ste.


there is also a simple solution with templates:

Hidden Text: Show

Code: Select all

initialization:

#VT: (1 1 3 9 3 27 5 4 167)
Cells: nil nil nil nil nil nil nil nil nil
Candidates:nil nil nil (54) nil nil nil nil nil

5      3469   3469   69     2      1      689    7      4689           
69     8      2      7      3      4      5      1      69             
469    1      7      69     8      5      2      3      469             
469    2      3469   1      479    8      3679   469    5               
7      459    4589   3      49     6      89     2      1               
1      3469   34689  5      479    2      36789  4689   6789           
2      579    1      4      6      79     789    589    3               
3      5679   569    8      1      79     4      569    2               
8      4679   469    2      5      3      1      69     679             


1: (5 8) 2 compatible instances:

5.......8.8....5......85........8..5..5...8....85......5.....8....8...5.8...5....
5.......8.8....5......85........8..5.58.........5...8.......85...58.....8...5....

leave these templates:

5..............5.......5...........5..5.........5......5..............5.....5....
5..............5.......5...........5.5..........5............5...5..........5....

........8.8...........8.........8.........8....8.............8....8.....8........
........8.8...........8.........8.....8.............8.......8.....8.....8........

and update the grid to this state:

#VT: (1 1 3 9 2 27 5 2 167)
Cells: nil nil nil nil nil nil nil (9) nil
SetVC: ( n8r1c9   n4r3c9   n4r4c1   n4r6c8   n4r5c5   n8r7c8
         n5r8c8   n5r7c2   n9r5c2   n8r5c7   n5r5c3   n8r6c3 )

#VT: (1 1 2 2 1 4 3 1 5)
Cells: nil nil nil nil nil nil nil nil nil
Candidates:nil nil nil nil nil (2 3 74 75) nil nil (3)

5     34    34    69    2     1     69    7     8             
69    8     2     7     3     4     5     1     69             
69    1     7     69    8     5     2     3     4             
4     2     36    1     79    8     3679  69    5             
7     9     5     3     4     6     8     2     1             
1     36    8     5     79    2     3679  4     679           
2     5     1     4     6     79    79    8     3             
3     67    69    8     1     79    4     5     2             
8     47    49    2     5     3     1     69    679           


2: (6 9) 2 compatible instances:

...6..9..9.......66..9.......6....9..9...6.......9.6......69....69.............69
...9..6..6.......99..6.......6....9..9...6.......9...6....6.9...6...9.....9....6.

leave these templates:

...6.............66..........6...........6.........6......6.....6..............6.
......6..6...........6.......6...........6...........6....6.....6..............6.

...9.............99...............9..9...........9..........9.......9.....9......
......9..9...........9............9..9...........9.........9.....9..............9

and update the grid to its solution:

#VT: (1 1 2 2 1 2 3 1 2)
Cells: nil nil nil nil nil (30 65 80) nil nil (35 50)
SetVC: ( n6r4c3   n9r4c8   n3r6c2   n9r6c5   n6r8c2   n9r8c3
         n7r8c6   n4r9c3   n6r9c8   n4r1c2   n3r1c3   n7r4c5
         n3r4c7   n9r7c6   n7r7c7   n7r9c2   n9r9c9   n6r2c9
         n6r6c7   n7r6c9   n9r1c7   n9r2c1   n6r3c1   n9r3c4
         n6r1c4 )
5 4 3   6 2 1   9 7 8
9 8 2   7 3 4   5 1 6
6 1 7   9 8 5   2 3 4
4 2 6   1 7 8   3 9 5
7 9 5   3 4 6   8 2 1
1 3 8   5 9 2   6 4 7
2 5 1   4 6 9   7 8 3
3 6 9   8 1 7   4 5 2
8 7 4   2 5 3   1 6 9


[Cenoman]

Code: Select all

 +-----------------------+------------------+------------------------+
 |  5     3469   3469    |  69   2     1    |  69-8    7      4689   |
 |  69    8      2       |  7    3     4    |  5       1      69     |
 |  469   1      7       |  69   8     5    |  2       3      469    |
 +-----------------------+------------------+------------------------+
 |  469   2      3469    |  1    479   8    |  3679    469    5      |
 |  7    a459    58-49   |  3   a49    6    | a89      2      1      |
 |  1     3469   34689   |  5    479   2    |  3679-8  4689   6789   |
 +-----------------------+------------------+------------------------+
 |  2    b579    1       |  4    6    b79   | b789     58-9   3      |
 |  3     679-5  569     |  8    1     79   |  4       569    2      |
 |  8     4679   469     |  2    5     3    |  1       69     679    |
 +-----------------------+------------------+------------------------+

1. Doubly linked ALS-XZ rule:
(5=498)r5c257 - (8=495)r7c267 loop => -9r7c8 -49r5c3, -5r8c2, -8r16c7; lcls, 12 placements

Code: Select all

 +-----------------+-----------------+--------------------+
 |  5   C34   34   |  69   2    1    | a69     7    8     |
 |  69   8    2    |  7    3    4    |  5      1    69    |
 |  69   1    7    |  69   8    5    |  2      3    4     |
 +-----------------+-----------------+--------------------+
 |  4    2    36   |  1    79   8    | a37+69  69   5     |
 |  7    9    5    |  3    4    6    |  8      2    1     |
 |  1  yB36   8    |  5    79   2    |Aa36+79  4   x79+6  |
 +-----------------+-----------------+--------------------+
 |  2    5    1    |  4    6    79   | b79     8    3     |
 |  3   z67   69   |  8    1    79   |  4      5    2     |
 |  8  zC47   49   |  2    5    3    |  1      69  a6-7+9 |
 +-----------------+-----------------+--------------------+

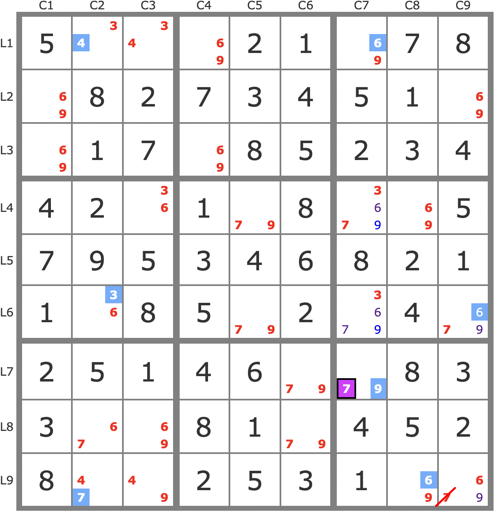
2. BUG+6
(69r14c7|9r4c7|9r9c9) - (9=7)r7c7
(7-3)r6c7 = r6c2 - (3=47)r19c2
(6)r6c9 - r6c2 = (67)r89c2
=> -7 r9c9; ste