The New Sudoku Players' Forum

[Wecoc]

1 to 9 Ascending Sudoku

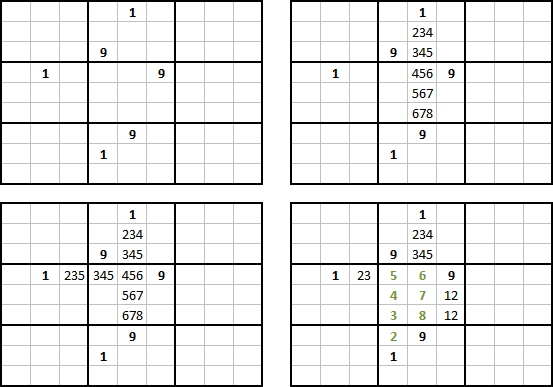
Here's a little challenge similar to the one I posted some months ago.
Consider a valid sudoku grid. There's a 1 and a 9 in each row and each column.
The extra constrain here is numbers from that 1 to the 9 on the same row/column must be always in ascending order.

By that I mean for example 13479, but not 14379.

Example: Show

Q- Is it possible a sudoku with this constrain which givens are only 1s and 9s, but with a unique valid solution?

[tarek]

If the 1 and 9 are always known than this is is just a special case of lesser than / greater than

[Mathimagics]

Yes, it is a special case of Sudoku Inequality (as I call it), and so is not really a new puzzle type, but the question of whether a valid puzzle exists with these attributes is still quite intriguing.

Firstly, it looks like the solution grid candidates are very rare - random sampling seems to suggest no more than 1 in 150,000 grids have the desired property (ascending /descending chains between the 1/9 pairs).

With the 1's and 9's as givens, we need a gap of at least 2 cells between them (in row or col) to provide non-trivial "less than/greater than" clues. Unfortunately none of the valid candidate grids I am finding have come close to having a unique solution.

Grid searching looks to be too slow, so I will try using a puzzle template approach ...